2004年温州中学数学试验班招生数学试卷
说明:
1、试卷满分120分;考试时间:2小时.
2、试卷共三大题,计18道题。考试结束后,将本卷及演算的草稿纸一并上交。
一、选择题(共8小题,每题4分,共32分)
1、记![]() …………………………… ( )
…………………………… ( )
A、一个奇数 B、一个质数
C、一个整数的平方 D、一个整数的立方
2、圆周上共有10个等分点,以其中三点为顶点的直角三角形的个数为………………( )
A、20 B、40 C、60 D、80
 3、如图1,已知⊙O的半径是R,C、D是直径AB同侧圆周上的两点,弧AC的度数为960,弧BD的度数为360,动点P在AB上,则PC+PD的最小值为………………………( )
3、如图1,已知⊙O的半径是R,C、D是直径AB同侧圆周上的两点,弧AC的度数为960,弧BD的度数为360,动点P在AB上,则PC+PD的最小值为………………………( )
A、2R B、![]() C、
C、![]() D、R
D、R
4、已知实数a,b,c满足![]() 则关于x的方程ax2+bx+c=0………………………………………………………( )
则关于x的方程ax2+bx+c=0………………………………………………………( )
A、有两个不相等的实数根 B、有两个相等的实数根
C、没有实数根 D、不能确定
5、如果一个凸多边形有且仅有三个内角是钝角,那么这种多边形的边数不可能是………………………………………………………………………………( )
A、4 B、5 C、6 D、7
6、用六根火柴棒搭成4个正三角形(如图2),现有一只虫子从点A出发爬行了5根不同的火柴棒后,到了C点,则不同的爬行路径共有………………………………………( )
A、4条 B、5条 C、6条 D、7条
 7、一次函数
7、一次函数![]() 的图象与x轴、y轴分别交于点A、B,O为坐标原点,则在△OAB内部(包括边界),纵坐标、横坐标都是整数的点共有…………………………………………( )
的图象与x轴、y轴分别交于点A、B,O为坐标原点,则在△OAB内部(包括边界),纵坐标、横坐标都是整数的点共有…………………………………………( )
A、90个 B、92个 C、104个 D、106个
8、如果![]() ,
,![]() 是正整数,则
是正整数,则![]() 的最小值是…( )
的最小值是…( )
A、15 B、17 C、72 D、144
二、填空题:(共4小题,每题4分,共16分)
9、设a,b为两个不相等的实数,且满足![]() ,则
,则![]() 的值是
的值是
10、如图3,直角梯形ABCD中,∠BAD=900,AC⊥BD,![]() ,则
,则![]()
 |
11、如图4,已知AG⊥BD,AF⊥CE,BD,CE分别是∠ABC和∠ACB的角平分线,若BF=2,ED=3,GC=4,则三角形ABC的周长是
12、设![]() 且
且![]()
则![]()
三、解答题(共6题,共72分)
13、(本题满分14分)
如果一个数能表示成![]() (
(![]() 是整数),我们称这个数为“好数”。
是整数),我们称这个数为“好数”。
(1)判断29是否为“好数”?
(2)写出1,2,3,…,20中的“好数”。
(3)如果![]() 都是“好数”,求证:
都是“好数”,求证:![]() 是“好数”。
是“好数”。
14、(本题满分8分)
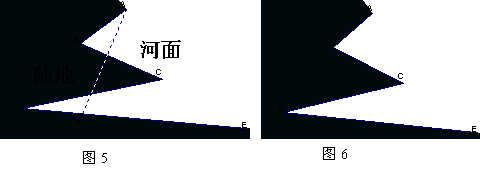
如图5所示,阴影部分是陆地,折线ABCDE是河岸,今要将河岸拉直,需在线段DE上找一点M,将河岸ABCDM变成线段AM,并且河面面积保持不变。
请你在图6中画出线段AM(保留作图痕迹),并说明理由。(本题8分)
 |
15、(本题满分12分)
 |
如图7,⊙O的弦AC、BD交于点Q,AP、CP是⊙O的切线,O、Q、P三点共线。求证:
16、(本题满分14分)
定义下列操作规则:
规则A:相邻两数a、b,顺序颠倒为b、a,称为一次“变换”。(如一行数1、2、3、4要变为3、1、2、4,可以这样操作:![]() 。)
。)
规则B:相邻三数a、b、c,顺序颠倒为c、b、a,称为一次“变换”。
规则C:相邻四数a、b、c、d,顺序颠倒为d、c、b、a,称为一次“变换”。
现按照顺序排列着1、2、3、…、2004、2005,目标是:经过若干次“变换”,将这一行数变为2005、1、2、…、2003、2004。
问:(1)只用规则A操作,目标能否实现?
(2)只用规则B操作,目标能否实现?
(3)只用规则C操作,目标能否实现?
17、(本题满分12分)
 |
如图8,O是Rt△ABC斜边AB的中点,CH⊥AB于H,延长CH至D,使得CH=DH,F为CO上任意一点,过B作BE⊥AF于E,连结DE交BC于G.
(1)求证:∠CAF=∠CDE;
(2)求证:CF=GF。
18、(本题满分12分)
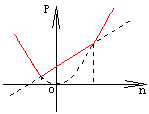
已知二次函数![]()
(1)若此二次函数的图象经过点(1,1),且记![]() 两数中较大者为P,试求P的最小值。
两数中较大者为P,试求P的最小值。
(2)若![]() 变化时,它们的图象是不同的抛物线,如果每条抛物线与坐标轴都有三个不同的交点,过这三个交点作圆,证明这些圆都经过同一定点,并求出这个定点的坐标。
变化时,它们的图象是不同的抛物线,如果每条抛物线与坐标轴都有三个不同的交点,过这三个交点作圆,证明这些圆都经过同一定点,并求出这个定点的坐标。
2004年温州中学数学实验班招生考试数学试卷
(参考答案及评分标准)
一、选择题:(每小题4分,共32分)
1~8.CBBAD,CDB
二、填空题:(每小题4分,共16分)
9、—27, 10、1/3 11、30 12、4
三、解答题(共6题,共72分)
13、(本题满分14分)
解答:![]()
(1)![]() ,29是“好数”。(4分)
,29是“好数”。(4分)
(2)1,2,3,…,20中的“好数”有1,2,4,5,8,9,10,13,16,17,18,20。(8分)
(3)设![]() ,
,![]() 是整数。
是整数。
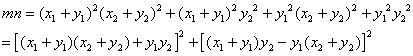
令![]() ,则
,则![]() 是整数,
是整数,
且![]() ,所以
,所以![]() 是“好数”。(14分)
是“好数”。(14分)
 14、(本题满分8分)
14、(本题满分8分)
解答:连接BD,过C作CF∥BD交DE于F,则![]() 。(6分)
。(6分)
连接AF,过B作BM∥AF交DE于M,则![]() ,连接AM即为所求。(8分)
,连接AM即为所求。(8分)
15、(本题满分12分)
 证明:连接OA、OB、OD,设DP交⊙O于E,设⊙O的半径为R,可证
证明:连接OA、OB、OD,设DP交⊙O于E,设⊙O的半径为R,可证![]() (4分)
(4分)![]() (8分)
(8分)
![]() 四点共圆,又OD=OB,
四点共圆,又OD=OB,![]() ,
,![]()
![]()
![]() 。(12分)
。(12分)
16、(本题满分14分)
解答:(1)能,实行如下操作:
![]() (4分)
(4分)
(2)不能,从左到右,把数所占的位置编上号,按照规则B,若数![]() 在
在![]() 号位置,一次变换后可能是
号位置,一次变换后可能是![]() 号位置,所以操作过程中数
号位置,所以操作过程中数![]() 所占位置的奇偶性不会改变。而1、2、3、…、2004、2005中1在1号位,目标2005、1、2、…、2003、2004中1是2号位,这不可能。(8分)
所占位置的奇偶性不会改变。而1、2、3、…、2004、2005中1在1号位,目标2005、1、2、…、2003、2004中1是2号位,这不可能。(8分)
(3)能,通过如下操作(记为“*操作”):

![]()
可以将一个数往前提4个位置,而其他各数的顺序不变。(12分)
将2001、2002、2003、2004、2005通过“*操作”,可以变为2005、2001、2002、2003、2004,再对1997,1998,1999,2000,2005施行“*操作”,变为2005、1997、1998、1999、2000,如此反复,1、2、3、…、2004、2005可以变为1、2、3、4、2005、5、6、…、2004,最后对1、2、3、4、2005施行“*操作”得到2005、1、2、…、2003、2004。(14分)
15、(本题满分12分)
[解答]:(1)证明:连结BD,

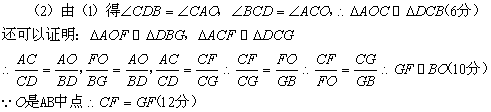
18、(本题满分12分)
[解答]:(1)由过点(1,1)得到:![]()
![]()
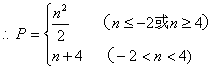 (3分)
(3分)
如图所示,当![]() 时
时![]() (6分)
(6分)

