一元二次方程单元检测
_____年级 ______班级 姓名_____________
一、填空题:(每空3分,共30分)
1、一元二次方程(x+1)(3x-2)=10的一般形式是 ________ ;当m __ 且m ___ 时,关于x的一元二次方程mx2-2x+1=0有两个不相等实数根。
2、如果一元二次方程ax2-bx+c=0有一个根为0,则c= ; 关于x的一元二次方程2x2-ax-a2=0有一个根为-1,则a=___
3、把一元二次方程3x2-2x-3=0化成3(x+m)2=n的形式是 _____;若多项式x2-ax+2a-3是一个完全平方式,则a= ______
4、已知关于x的方程x2+px-6=0的一根为2,则另一个根为 ___,p= .
5、已知关于x的方程x2+px-6=0的两实数根的平方和等于16,则p的值为 ________
方程x2-5x-6=0的两根为![]() ,则(
,则(![]() 2-2
2-2![]() )(
)(![]() )= .
)= .
6、以2+![]() 和2-
和2-![]() 为两根的一元二次方程是 ______________
为两根的一元二次方程是 ______________
7、设2x2-4x-5=0的两根为x1、x2, 则以2x1、2x2为两根的一元二次方程是 ___________
8、关于x的一元二次方程x2-mx+12=0的两根之差为11,则m= ;关于x的一元二次方程3x2-20x+3k+1=0的一根是另一根的3倍,则k=
二、选择题:(每小题3分,共30分)
1、对于任意实数x,多项式x2-5x+8的值是一个 ( )
A.非负数 B.正数 C.负数 D.无法确定
2、方程x2-2003x+2002=0的两根为![]() , 则代数式(a2-2002a+2002)(
, 则代数式(a2-2002a+2002)(![]() -2004
-2004![]() +2002)的值是 ( )
+2002)的值是 ( )
A.2003 B.2002 C.-2003 D.-2002
3、方程x2+ax+1=0和x2-x-a=0有一个公共根,则a的值是 ( )
A.0 B.1 C.2 D.3
4、关于x的一元二次方程(k2+1)x2-2kx-1=0的根的情况是( )
A.有两个正根 B.有两个负根
C.有一正根、一负根 D.无实数根
5、若实数a、b满足a2=2-2a,b2=2-2b,则a/b+b/a的值为 ( )
A-5 B.-1+![]() C.-4或2
D.2
C.-4或2
D.2
6、若m、n为方程x2+2x-2003=0的两个实数根,则m2+3m+n的值 A.2000 B.2001 C.2002 D.2003 ( )
7、已知等腰三角形的三边长分别为a、b、c,且a=c,若关于
x的一元二次方程ax2+![]() bx+c=0的两个根之差为
bx+c=0的两个根之差为![]() ,则等腰
,则等腰
三角形的一个底角是 ( )
A.150 B.300 C.450 D.650
8、在解分式方程![]() 时,若设
时,若设![]() ,则原方程
,则原方程
可以化为y关于的整式方程为 ( )
A.2y+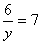 B.
B.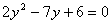 C.
C.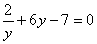 D.
D.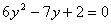
9、方程 3x2+5x=0的实数根是 ( )
A.x=0 B.x=![]() C. x1=0,
x2=
C. x1=0,
x2=![]() D. x1=0, x2=
D. x1=0, x2=![]()
10、一元二次方程x2+px+q=0的两根分别为3和4,那么二次
三项式x2-px+q=0可分解为 ( )
A.(x+3)(x+4) B.(x-3)(x+4) C.(x-3)(x-4) D.(x+3)(x-4)
三、用适当的方法解下列方程:(每小题4分,共24分)
1、![]() 2、2x2+x-1=0
2、2x2+x-1=0
3、2x2=5x-1
4、(y+2![]() )2=8
)2=8![]() y
y
5、(x+4)(3x-2)+11=0 6、4(x+2)2=9(2x-1)2
四、解答题:(每小题5分,共15分)
1、方程x2-2ax+a2-4=0的两根都是正数,且大根是小根的5倍,求这两根及a的值。
2、已知a、b为不相等的两个实数,且2a2=5-3a, 2b2=5-3b, 求(a-2)(b-2)的值。
3、若m:n=(x+y):(x-y),且m≠n, 求x2:y2.(用m、n表示)
五、(1)、某县位于沙漠边缘地带,治理沙漠、绿化家园是全县人民的共同愿望。到2002年底全县沙漠的绿化率已达30%,此后,政府计划在几年内,每年将当年年初未被绿化的沙漠面积的m%栽上树进行绿化,到2004年底全县沙漠绿化率已达43.3%,求m的值.(本题8分)
(2)在△ABC 中,∠A=900,AB=6,AC=8. 点P从A开始沿AC向C匀速运动,点Q从点A开始沿AB边点B,再沿BC向点C匀速运动。若P、Q两点同时从点A出发,则可同时到达C.
⑴如果P、Q两点同时从点A出发,以原速度按各自的移动路线移动到某一时刻同时停止移动,当点Q移动到BC边上(Q不与C重合),求作以tan∠QCA, tan∠QPA为根的一元二次方程。
 ⑵如果P、Q两点同时从点A出发,以原速度按各自的移动路线移动到某一时刻,同时停止移动,当S△PBQ=
⑵如果P、Q两点同时从点A出发,以原速度按各自的移动路线移动到某一时刻,同时停止移动,当S△PBQ=![]() , 求PA的长。(本题13分)
B
, 求PA的长。(本题13分)
B
A C
