《圆》测试卷 姓名
一、选择
1、下列命题正确的是（ ）
A．相等的圆心角所对的弦相等 B．等弦所对的弧相等
C．等弧所对的弦相等 D．垂直于弦的直线平分弦
2、如图1－3－7，A、B、C是⊙O上的三点，∠BAC=30°
则∠BOC的大小是（ ）
A．60○ B．45○
C．30○ D．15○
3、四边形 ABCD内接于⊙O，若∠BCD=100°，则
∠DAB的度数为（ ）
A．50° B．80° C．100° D．130°
4、Rt△ABC中，∠C=90°，∠AC=3cm，BC＝4cm，给出下列三个结论：
① 以点C为圆心，1．3 cm长为半径的圆与AB相离；
② 以点C为圆心，2．4cm长为半径的圆与AB相切；
③ 以点C为圆心，2．5cm长为半径的圆与AB相交．
上述结论中正确的个数是（ ）
A．0个 B．l个 C．2个 D．3个
5、两个同心圆的半径分别为1cm和2cm，大圆的弦AB与小圆相切，那么AB=（ ）
A． B．2 C．3 D．4
6、已知⊙O1和⊙O2的半径分别为3 cm和5 cm，两圆的圆心距是6 cm，则这两圆的位置关系是（ ）
A．内含 B．外离 C．内切 D．相交
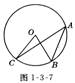
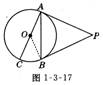
7、如图l－3－17，已知PA，PB是⊙O的切线，A、B为切点，AC是⊙O的直径，∠P=40°，则∠BAC度数是（ ）
A．70° B．40° C．50° D．20°
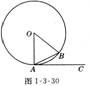
8、如图1－3－30，A、B是⊙上的两点，AC是⊙O的切线，
∠B＝65○ ，则∠BAC等于（ ）
A．35○ B．25○ C．50○ D．65○
9、已知Rt△ABC的斜边AB=5，一条直角边AC=3，以直线BC为轴旋转一周得到一个圆锥，则这个圆锥的侧面积为（ ）
A．8π B．12π C．15π D．20π
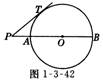
10、如图1－3－42，PT切⊙O于点T，经过圆心O的割线PAB交⊙O于点A 、B，已知PT=4，PA=2，则⊙O的直径A B等于（ ）
A．3 B．4 C．6 D．8
二、填空
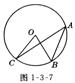
11、如图1－3－l，在⊙O中，已知∠ACB＝∠CDB＝60○ ，
AC＝3，则△ABC的周长是 .
 | |||||
 |  | ||||
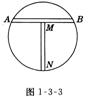12、如图l－3－3，MN所在的直线垂直平分弦A B，利用这样的工具最少使用 次，就可找到圆形工件的圆心．
13、在△ABC中，∠A=62°，点I是外接圆圆心，则∠BIC=
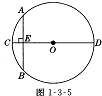
14、“圆材埋壁”是我国古代《九章算术》中的问题：“今有圆材，埋在壁冲，不知大小，以锯锯之，深一寸，锯道长一尺，间径几何”．用数学语言可表述为如图1－3－5，CD为⊙O的直径，弦AB⊥CD于点E，CE＝1寸，AB=10寸，则直径CD的长为 寸。
15、已知相切两圆的半径分别为3cm和2cm，则两圆的圆心距
是 cm．
16、如图1－3－7，在⊙O中，弦AB=BC=5cm，AC=8cm，则⊙O的半径等于 cm．
17、粮仓顶部是圆锥形，这个圆锥的底面圆的周长为36m，母线长为8m．为防雨需在粮食顶部铺上油毡，需要铺油毡的面积
是 好．
18、如图1－3－50，⊙O的半径为1，圆周角∠ABC=30°，则图中阴影部分的面积是 .
 |  | ||||||
 |  | ||||||
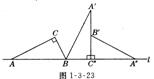
19、如图1－3－23，把直角三角形 ABC的斜边AB放在定直线l上，按顺时针方向在l上转动两次，使它转到△A″B′C″的位置，设BC=1，AC=，则顶点A运动到 A″的位置时，点A经过的路线与直线l所围成的面积是 。
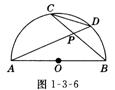20、如图1－3－6，已知AB是半圆O的直径，弦AD和BC相交于点P，∠BPD=60°那么等于 。
三、解答
21、⊙O的半径是5，AB、CD为⊙O的两条弦，且AB∥CD，AB=6，CD=8，求 AB与CD之间的距离。
22、如图l－3－19，PA切⊙O于A，PB切⊙O于B，
∠APB=90°，OP=4，求⊙O的半径。
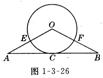23、如图1－3－26，△ABO中，OA= OB，以O为圆心的圆经过AB中点C，且分别交OA、OB于点E、F．
（1）求证：AB是⊙O切线；
（2）若△ABO腰上的高等于底边的一半，且AB=4，求弧ECF的长。
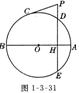
24、图 1－3－31，⊙ O的直径AB=10，DE⊥AB于点H，A H=2．
（1）求DE的长；
（2）延长ED到P，过P作⊙O的切线，切点为C，若PC=2，求PD的长。
 |
25、如在在⊙O中，AB是直径，半径为R，弧AC
求：
(1)∠AOC的度数；
(2)若D为劣弧BC上的一动点，且弦AD与半径OC交于E点.试探求△AEC≌△DEO时，D点的位置。
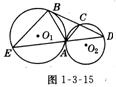
附加：⊙O1和⊙O2外切于点A，直线BD切 ⊙O1于点B，交⊙O2于点 C、D，直线 DA交⊙O1于点 E．
求证：（1）∠BAC=∠ABC+∠D （2）AB2=AC·AE．
