初三数学月考试卷(2006.3)
一.选择题(每题3分,共计24分)
| 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 |
1. 下列运算正确的是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2. 粤海铁路是我国第一条横跨海峡的铁路通道,设计年输送货物能力为11 000 000吨,用科学记数法应记为( )
A、11×106吨 B、1.1×107吨 C、11×107吨 D、1.1×108吨
3. 实数![]() ,sin30º,
,sin30º,![]() +1,
+1,![]() ,(
,(![]() )0,-3中,有理数的个数是( )
)0,-3中,有理数的个数是( )
A、2个 B、3个 C、4个 D、5个
4. 不解方程,判别方程5![]() -7x+5=0的根的情况是(
)
-7x+5=0的根的情况是(
)
A、有两个相等的实数根 B、有两个不相等的实数根
C、只有一个实数根 D、没有实数根
5. 一列列车自2004年全国铁路第5次大提速后,速度提高了26千米/时,现在该列车从甲站到乙站所用的时间比原来减少了1小时,已知甲、乙两站的路程是312千米,若设列车提速前的速度是x千米,则根据题意所列方程正确的是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
6. 如果关于x的方程(a+1)x + 1= 0有负根,则a的取值范围是( )
A、a>-1 B、a<-1 C、a≥-1 D、a≤-1
7. 用换元法解方程![]() ,若设
,若设![]() ,则原方程化为整式方程是( )
,则原方程化为整式方程是( )
A、![]() B、
B、![]()
C、![]() D、
D、![]()
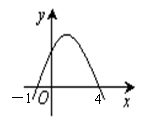 8. 二次函数y = ax2+ bx + c的图象如图所示,那么关于此二次 函数的下列四个结论:
8. 二次函数y = ax2+ bx + c的图象如图所示,那么关于此二次 函数的下列四个结论:
① a<0;②c>0;③b2-4ac>0;④2a+b<0中,正确的有 ( )
A、1个 B、2个 C、3个 D、 4个
二.填空题(每题3分,共计24分)
9. -![]() 的相反数是
的相反数是
10. 函数![]() 中,自变量
中,自变量![]() 的取值范围是_________
的取值范围是_________
11. 分解因式![]()
12. 若![]() 、
、![]() 是一元二次方程
是一元二次方程![]() 的两根,则x
的两根,则x![]()
![]() + x
+ x![]()
![]() 的值是
的值是
13. 适合![]() =3―a的正整数a的值有
个
=3―a的正整数a的值有
个
14. 将抛物线y=2(x-4)2-1向 平移 个单位,向 平移 个单位可得抛物线y=2x2
15. 若关于![]() 的方程
的方程![]() 有增根,则
有增根,则![]() 的值是
的值是
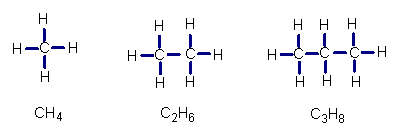 16. 下列是三种化合物的结构式及分子式,请按其规律,写出后一种化合物的分子式
16. 下列是三种化合物的结构式及分子式,请按其规律,写出后一种化合物的分子式
三.计算题(17、18、19题每题5分,20题6分,共计21分)
17. ![]()
18. 解分式方程 ![]()
20.解不等式组
 并把解集在数轴上表示出来
并把解集在数轴上表示出来
20.先化简,再求值
![]() ,其中a=3时。
,其中a=3时。
四.解答题(21题7分,22、23、24题每题8分,共计31分)
21.  如图,一次函数
如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数
![]() 的图象交于M、N两点.
的图象交于M、N两点.
(1)求反比例函数和一次函数的解析式;
(2)根据图象写出使反比例函数的值大于一次函数的
值的x的取值范围.
22. 已知关于x的方程x![]() +2kx+
+2kx+![]() k
k![]() -2=0
-2=0
(1) 求证:不论k取什么实数值,方程总有两个不相等的实数根;
(2) 设x![]() , x
, x![]() 是方程的两实根,且x
是方程的两实根,且x![]()
![]() +2kx
+2kx![]() +2 x
+2 x![]() x
x![]() = 12。.求k的值。
= 12。.求k的值。
23.已知抛物线与x轴交于A(-1,0)和B(3,0)两点,且与y轴交于点C(0,3)求:
(1)抛物线的解析式;(2)抛物线的对称轴方程和顶点M坐标;(3)四边形ABMC的面积
26. 我国的东南沿海某地的风力资源丰富,一年内日平均风速不小于3m/s的时间工约160d,其中日平均风速不小于6m/s的时间约占60d.
为了充分利用“风能”这种“绿色能源”,该地拟建一个小型风力发电场,决定选用A,B两种型号的风力发电机。根据产品说明,这两种风力发电机在各种风速下的日发电量(即一天的发电量)如下表:
| 日平均风速v/(m/s) | V<3 | 3≤v<6 | v≥6 | |
| 日发电量/(kw·h) | A型发电机 | 0 | ≥36 | ≥150 |
| B型发电机 | 0 | ≥24 | ≥90 | |
根据上面的数据回答:
(1)若这个发电场够x台B型风力发电机,则预计这些B型风力发电机一年的发电总量至少为 kw·h
(2)已知A型风力发电机每台0.3万元,B型风力发电机每台0.2万元。该发电场拟购置风力发电场10台,希望购机费用不超过2.6万元,而建成的风力发电场每年的发电总量不少于102000 kw·h。请你提供符合条件的购机方案。
