2006年浙江省金华市课改实验区学业考试调研测试卷

数　 学

考生须知：

1．全卷共三大题，24小题，满分为150分。考试时间为100分钟。本次考试采用开卷形式。

2．全卷分试卷Ⅰ（选择题）和试卷Ⅱ（非选择题）两部分。答案都必须做在“答题卷”的相应位置上。

3．用蓝、黑颜色钢笔或圆珠笔在“答题卷”密封区内填写县（市、区）、学校、姓名和学号。

试　卷　Ⅰ

一. 选择题（本题共10小题，每小题4分，共40分，请选出各题中一个符合题意的正确选项，不选、多选、错选均不给分）

1.－3的相反数是（▲）

A. 　　　　　　B.　－3　　　　　 C.　－　　　  D.　3

2. 方程2x＋3＝7的解是（▲）

A.　x＝2　　　　 B.　x＝－2　　　  C.　x＝1　　　　 D.　x＝－1

3. 去年，浙江省国民生产总值达到13340亿元，这个数用科学记数法可表示为（▲）

A.　13.34×10⁴亿元　　　　　　　　 B.　1.334×10⁴亿元

C.　0.1334×10⁵亿元　　　　　　　  D.　1.334×10⁵亿元

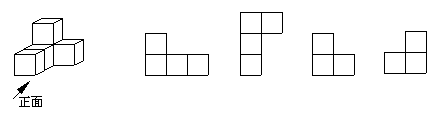4. 图中几何体的主视图是（▲）

A.　　　　 B.　　　　 C.　　　　 D.

5 .如图是某城市居民家庭人口数的统计图，那么这个城市家庭人口数的众数是（▲）

A.　2人　　　　　 B.　3人　　　　 

C.　4人　　　　　 D.　5人

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

6.下列说法正确的是（▲） 　　　　　　　　　　　　　　　　　　

A.　在同一年出生的400人中至少有两人的生日相同

B.　一个游戏的中奖率是1％，买100张奖券，一定会中奖 　　 

C.　一副扑克牌中，随意抽取一张是红桃K，这是必然事件

D.　一个袋中装有3个红球、5个白球，任意摸出一个球是红球的概率为

7.下列四个生活、生产现象：①用两个钉子就可以把木条固定在墙上；②植树时，只要定出两棵树的位置，就能确定同一行树所在的直线；③从A地到B地架设电线，总是尽可能沿着线段AB架设；④把弯曲的公路改直，就能缩短路程. 其中可用公理“两点之间，线段最短”来解释的现象有（▲）

A.　①②　　　　 B.　③④　　　　  C.　①③　　　　  D.　②④

8. 已知点A（－1，y₁），点B（2，y₂）在函数y＝－3x＋2的图象上，那么y₁与y₂的大小关系是（▲）

A.　y₁＞y₂　　　  B.　y₁＜y₂　　　　 C. y₁＝y₂　　　D.　不能确定

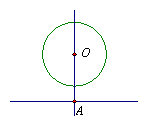9. 如图，⊙O的半径为2cm，过点O向直线l引垂线，垂足为A，OA的长为3cm，将直线l沿AO方向平移，使直线l与⊙O相切，那么平移的距离为（▲）　　　　　　　　　　  　　　　　　　　　　　　　　　

A.　1cm　　　　  B.　3cm　　　　

C.　5cm　　　  D.　1cm或5cm　　　　　　　　　　　　　　　

10. 已知点P（2－a，3a）在第四象限，那么a的取值范围为（▲）

A. 0＜a＜2　　　 B.　a＜0　　　　　 C. a＞2　　　D. －2＜a＜0　

试　卷　Ⅱ

二、填空题（本题有6小题，每小题5分，共30分）

11. 小明和小新在同一街道，如果小明家在学校的东面600米处记作＋600米，那么小新家在学校的西面200米处，记作 ▲ 米.

12. 如图，AC是半圆O的直径，点B在半圆上，

如果∠A＝20°，那么∠COB＝ ▲ °.

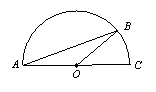（第12题图）　　　　　　　　　　 （第13题图）　　　　　　　 （第15题图）

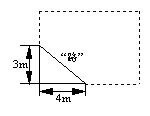
13. 如图，学校有一块长方形花坛，有极少数人为了避开拐角走“捷径”，在花坛内走出了一条“路”. 他们仅仅少走了▲ m，却踩伤了花草.

14. 已知反比例函数y＝的图象在第一、三象限内，那么k的值可为 ▲ .（写出满足条件的一个k的值即可）

15. 同学们都喜欢老师给他的作业打“红钩”. 我们将一张长10cm，宽1cm的矩形红纸条（图甲）进行翻折，也可得到一个漂亮的“红钩”（图乙）. 如果“红钩”中的∠＝60°，那么这个“红钩”的面积为 ▲ cm². （精确到0.1cm²）

16. 一电子跳蚤在数轴上从原点开始，第1次向右跳1个单位，紧接着第2次向左跳2个单位，第3次向右跳3个单位，第4次向左跳4个单位，……，依此规律跳下去，当它跳第7次和第2006次落下时，落点处离原点的距离分别是 ▲ 个单位.

三、解答题（本题有8小题，共80分，各小题都必须写出解答过程）

17．（本题8分）⑴计算：－1＋(－1)⁰－2^－1；

⑵先化简，后求值：÷，其中m＝－2.

8. （本题8分）如图，梯形ABCD中，AD∥BC，AB＝DC， E，F分别是AB，DC上的点，连接BF，CE. 请你增加一个条件（不再添加其它线段，不再标注或使用其他字母），使BF＝CE，并加以证明.

你添加的条件是： ▲ ；

证明：

19.（本题8分）小明和小亮玩一个游戏：三张大小、质地都相同的卡片上分别标有数字1，2，3，现将标有数字的一面朝下扣在桌子上. 小明从中任意抽取一张，记下数字后放回洗匀，然后小亮从中任意抽取一张.

⑴ 用列表或画树状图等方法，列出小明和小亮抽得的卡片上所标数字的所有可能情况；

⑵ 计算小明和小亮抽得的两张卡片上的数字之和，如果和为奇数则小明胜，和为偶数则小亮胜，请判断游戏是否公平，并说明理由.

20.（本题8分）同学们对公园的滑梯很熟悉吧！如图是某公园新增设的一台滑梯，该滑梯高度AC＝2m，滑梯着地点B与梯架之间的距离BC＝3m．

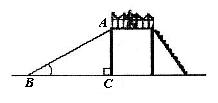⑴ 求滑梯AB的长（结果保留根号）；

⑵ 若规定滑梯的倾斜角（∠ABC）不超过45°属于安全范围．请通过计算说明滑梯的倾斜角是否符合要求？

21.（本题10分）在△ABC中，沿着中位线DE剪切后，用得到的△ADE和四边形DBCE可以拼成DBCF，剪切线与拼图如图1所示. 仿照上述的方法，按要求完成下列操作设计，并在规定位置画出图示. （画图工具不限，剪切线用实线表示，拼接线用虚线表示，要求写出简要的说明）

⑴ 将ABCD剪切成两个图形，再将它们拼成一个矩形，剪切线与拼图画在图2的位置；

⑵ 将梯形ABCD剪切成两个图形，再将它们拼成一个平行四边形，剪切线与拼图画在图3的位置.

22.（本题12分）我市居民生活用电的计费标准是：如果一个月的用电量不超过50度，那么每度电价为0.53元；如果一个月的用电量超过50度但不超过200度，那么未超过50度的部分每度电价仍为0.53元，超过50度的部分每度电价为0.56元. 小红将家里2005年下半年每月的用电量用折线图表示（如图），同时将相应电费制成下面的表格.

月份	电费（元）
7月	47.22
8月	42.18
9月	34.90
10月
11月
12月	49.46

根据上述信息，解答下列问题：

JH 数学试卷　第3页（共4页）

⑴ 小红家2005年下半年月用电量的平均数是 ▲ 度，中位数是 ▲ 度；

⑵ 计算小红家2005年10月份、11月份的电费；

⑶ 今年1月份小红家用电量较大，电费为65.7元，请你帮小红算一下，她家今年1月份的用电量是多少度？

23.（本题12分）小明家打算建一个苗圃，苗圃的两边靠墙（这两堵墙互相垂直），另外的部分用30米长的篱笆围成. 小明的爸爸提出一个问题：怎样围才能使苗圃的面积尽可能地大？小明思考后，设计了以下三种方案：

方案一：围成斜边为30米的等腰直角三角形（如图1）；

方案二：围成边长为15米的正方形（如图2）；

方案三：围成直角梯形，其中∠BCD＝120°（如图3）.

解答下列问题：

⑴ 分别计算方案一、方案二中苗圃的面积S₁，S₂，并比较S₁，S₂的大小；

⑵ 设方案三中CD的长为x米，苗圃的面积为S₃平方米，求S₃与x之间的函数关系式，并求出S₃的最大值；

⑶ 请你设计一种方案，使围成的苗圃面积比上述三个方案中的任何一个面积都大.（要求在图4中画出草图，标上必要的数据，并通过计算加以说明）

24.（本题14分）在直角坐标系中，O为坐标原点，点A的坐标为（2，2），点C是线段OA上的一个动点（不运动至O，A两点），过点C作CD⊥x轴，垂足为D，以CD为边作如图所示的正方形CDEF. 连接AF并延长交x轴的正半轴于点B，连接OF.

⑴ 求∠FOB的正切值；

⑵设OD＝t，用含t的代数式表示△OAB的面积；

⑶ 当以B，E，F为顶点的三角形与△OFE相似时，求经过O，A，B三点的抛物线解析式.