二次函数

二. 重点、难点：

二次函数的图像与性质以及二次函数在实际问题与综合问题中的应用。

三. 知识回顾。

1. 复习二次函数的三种解析式、开口，顶点、对称轴等基本概念

2. 复习二次函数的代数与几何两方面的性质

3. 体会在二次函数的学习中，对图像与性质的研究渗透了数形结合思想；求解析式时应用了待定系数法和配方法；在实际问题的求解中应用了分类讨论法等数学思想和方法。

4. 二次函数在实际问题中的应用，首先是合理、正确的建模，随后才是求解。

【典型例题】

例1. 已知a、b、c为实数，4a－4b＋c>0，a＋2b＋c<0，试比较b与ac的大小

解析：已知条件使人联想到二次函数模型中，自变量取两个不同的值所对应的函数值的结构特征，故构造二次函数求解即可。

设y＝

则①a＝0时，　∴　∴－6b>0　　∴b<0

又　ac＝0　　 ∴

②a时，当x＝2时 ；当x＝－1时，

∴抛物线与x轴定有两个不同的交点 。　∴　 ∴

∴由①、②知

例2. 设，且a为实数，3b＝a（3a－8），求整数b的个数。

解析：只有先求出b的取值范围，才能从这个范围中找出符合题设条件的整数b有几个。

∵3b＝a（3a－8）＝3a（）　（）

∴这是一个开口向上，顶点为（）的抛物线模形

又a＝5时，b＝　 ∴当时，

∴整数b＝、0、2、3、4…、11共计有13个。

例3. （如图）ΔABC中，∠C＝90º，AC＝BC＝3，动点P在AB上，过P作PE⊥AC于E，PF⊥BC于F，设CF＝x，问：是否存在这样的点P，使RtΔAEP，RtΔPFB以及矩形ECFP的面积都小于4？

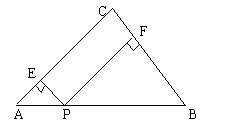
解：由题意，可得S ，不妨分别设为y₁，y₂和y₃

解y₁，y₂组成的方程组，得交点O（0，0），A（

解y₂，y₃组成的方程组，得交点B（，C（

据此，画出草图，从图中不难看出0≤x≤时，y₃≥4；<x≤时，y₁≥4；

　　≤x<时，y₂≥4

∴综上所知，当0<x<时，y₁，y₂，y₃的最大值不都小于4；

∴不存在这样的点P，使满足题设的条件。

【模拟试题】（答题时间：30分钟）

1. 已知抛物线y＝ax²＋bx＋c与y轴交于点（0，2），与x轴两交点的横坐标之和比它们的积的8倍小1，求a的取值范围。

2. 设抛物线y＝－3x²－2kx＋k²与双曲线在第二象限中一个交点的横坐标为－2，求k的值以及两图像交点的个数。

3. 抛物线y＝ax²＋bx＋c(a≠0) 图像的最高点的纵坐标是1，试化简代数式a＋

4. ΔABC中，∠C＝90º，AC＝6，BC＝8，M为BC中点，P是AB上一个动点（可与A、B重合），若∠MPD＝90º，PD交BC（或　 其延长线）于D，设BP＝x，y＝，问：是否存在这样的点P，使得ΔMPD∽ΔABC？若存在，求x的值；否则，请说明理由。

5. 抛物线y＝x²－2(k－1)x－1－k与x轴交于A（，0）B（，0），< 0 <，与y轴交于C，且，问：是否存在直线y＝与抛物线交于P，Q，使y轴平分ΔCPQ的面积？若存在，求，b所满足的条件；若不存在，请说明理由.

请做完之后，再看答案

【试题答案】

1. a>32 或 a<8 且a≠0

2. k＝－7，共有3个交点

3. 1－c

4. 存在，x＝或 提示：由题设条件，可求得y＝（0<x≤或5<x≤10）

∴若ΔMPD∽ΔACB时，可解得x＝；ΔMPD∽ΔBCA时，可解得x＝；

但若∠CMP＝∠A时，符合条件的点P不存在.

5. 存在.＝－2且b>－3.

提示：由题设条件，可先求得函数的解析式为y＝x²－2x－3,又由y轴平分ΔCPQ的面积可求得结论＝－2且b>－3。