第十七届中国数学奥林匹克 (2002年)
上海1月27日-28日早上8:00-12:30，每题21分。

1. 三角形ABC的三边长分别为a、b、c，b<c，AD是角A的内角平分线，点D在边BC上。
1. 求在线段AB、AC内分别存在点E、F(不是顶点)满足BC=CF 和∠BDE=∠CDF的充份必要条件(用角A、B、C表示)；
2. 在点E和F存在的情况下，用a、b、c表示BE的长。
2. 设多项式序列{ P_n(x) }满足：P₁(x)=x²-1，P₂(x)=2x(x²-1)，且
   P_n+1(x)P_n-1(x)=( P_n(x) )²-(x²-1)²，n=2, 3, ....。
   设S_n为P_n(x)各项系数的绝对值之和，对于任意正整数n，求非负整数k_n使得2^-k_nS_n为奇数。
3. 18支足球队进行单循环赛，即每轮将18支球队分成9组，每组的两队赛一场，下一轮重新分组进行比赛，共赛17轮，使得每队都与另外17支队各赛一场。按任意可行的程序比赛了n轮之后，总存在4支球队，它们之间总共只赛了1场。求n的最大可能值。
4. 对于平面上任意四个不同点P₁、P₂、P₂、P₄，求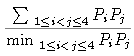的最小值。
5. 平面上横纵坐标都为有理数的点称为有理点。证明平面上的全体有理点可以分为三个两两不相交的集合，满足条件：
1. 在以每个有理点为圆心的任一圆内一定包含这三个集个中每个集合的点。
2. 在任意一条直线上不可能有三个点分别属于这三个集合。
6. 给定实数c，1/2<c<1，求最小的常数M，使得对任意整数n≧2，及实数0<a₁≦ a₂≦ ....≦ a_n，只要满足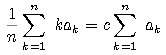，总有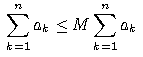，其中m不超过cn的最大整数。