九年级数学单元检测试卷
一、选择题（10×3＝30分）
1．在△ABC中，∠C＝90O，∠B＝2∠A，则CosA等于（ ）
A.
B. 
C. 
D. 
2.在△ABC中，∠C＝90O，BC：CA＝3：4，那么SinA等于（ ）
A．
B.
C.
D.
3.二次函数y＝（X－1）2＋2的最小值是（ ）
A．－2 B.2 C.1 D.－1
4．二次函数y＝ax2＋bx＋c的图像如图（1）所示，根据图像可得a，b，c与0的大小关系是（ ）
A. a>0,b<0,c<0 B. a>0,b>0,c>0 C. a<0,b<0,c<0 D. a<0,b>0,c<0
5.已知∠A为锐角，且COSA≤，那么（ ）
A．00<A≤600 B.600≤A<900 C.00<A<300 D.300≤A<900
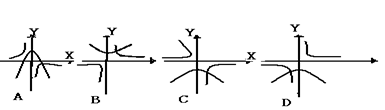
6.函数y＝ax2－a与y＝
（a≠0）在同一直角坐标系中的图像可能是图（2）中的（ ）
 |
7．已知二次函数y＝x2＋（2a＋1）x＋a2－1的最小值为O，则a的值是（ ）
A． B.
C.
D.
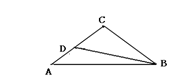8．如图（3）在等腰三角形ABC中，∠C＝900，AC＝6，D是AC上一点，若tan∠DBA＝
，则AD的长为（ ）
A.
B.2
C.1 D.2
9．将进货单价为70元的某种商品按零售价100元一个售出时，每天能卖出20个，若这种商品在一定范围内每降价1元，每日销量就增加1个，为了获得最大利润，则应该降价（ ）
A.5元 B.10元 C.15元 D.20元
10．某二元方程的解是
，若把x看作平面直角坐标系中点的横坐标，y看作是纵坐标，下面说法正确的是（ ）
A.点（x,y）一定不在第一象限 B.点（x,y）一定不是坐标原点
C.y随x的增大而增大 D.y随x的增大而减小
二．填空题：（8×3＝24分）
11．∠A和∠B是一直角三角形的两锐角，则tan
＝_________
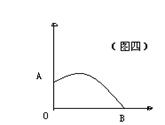
12．如图（4），某中学生推铅球，铅球在点A处出手，在点B处落地，它的运行路线满足y＝－
x2＋
x＋
，则这个学生推铅球的成绩是_______米
13．把抛物线y＝ax2+bx+c的图像向右平移3个单位，再向下平移2个单位，得到图像解析式为y=x2-4x+5，则有a=______ b=_______ c=_______
14.已知等腰三角形腰长为2cm，面积为1cm，则这个等腰三角形的顶角为_______度。
15．已知点A（x1,y1），B（x2,y2）是抛物线y＝x2－4x＋3上的两点，且x1>x2>2,则y1与y2的大小关系是___________
16．若函数y＝（m＋2）x ＋2x－3的图像是抛物线，则m的值为_______该抛物线的开口方向_________
17．心理学家发现，学生对概念的接受能力y与提出概念所用时间x（分）之间满足关系，y＝－0.1x2+2.6x+43(0≤x≤30)y值越大，表示接受能力越强，在第________分钟时，学生接受能力最强。
18．一辆骑车沿着一山坡行使了1300米，其铅直高度上升了500米，则山坡的坡度是______
三．解答题（66分）
19．计算sin2250＋2sin600＋tan450－tan600＋cos2250
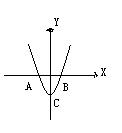20．二次函数y＝x2－1与x轴交于A.B两点，与y轴交于点c，试求△ABC的面积（7分）
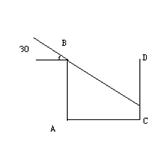21．如图（5）为住宅区的两栋楼，它们的高AB＝CD＝30m，两楼间的距离为AC＝24米，现需了解甲楼对乙楼的采光影响情况。当太阳光与水平线的夹角为300时求甲楼的影子在乙楼上有多高（10分）
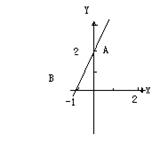
22．如图（6）直线y＝2x＋2与x轴，y轴分别相交于A、B两点，将△AOB绕点O顺时针旋转900得到（10分）
（1）在图中画出△A1OB1
（2）求经过A，A1，B1三点的抛物线的解析式。
 |
24．某船以每小时36海里的速度向正东航行，在A点测得某岛C在北偏东600方向上，航行半小时后到B点，测得C岛在北偏东300方向上，已知该岛周围16海里内有暗礁（10分）
（1）试说明B点是否在暗礁区域外
（2）若船继续向东航行，有无触礁危险，请说明理由。
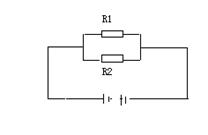
25．如图（7）已知电阻R1，R2并联在电路中，且R1＋R2＝10Ω，请用所学过的数学知识讨论一下R1，R2分别为多少时，该电路的总电阻最大，最大电阻是多少？（12分）
 |
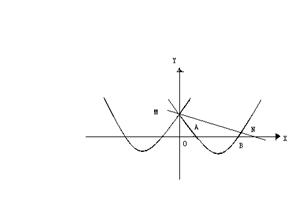
26．如图（8）已知抛物线y＝mx2＋nx＋p与y＝x2＋6x＋5关于y轴对称，并与y轴交于点M，与x轴交于点A和B（12分）
（1）求出y＝mx2＋nx＋p的解析式，试猜想出一般形式y＝ax2＋bx＋c关于y轴对称的二次函数解析式（不要求证明）
（2）若AB中点是C，求sin∠CMB
（3）如果一次函数y＝kx＋b过点M，且于y＝mx2＋nx＋p相交于另一点N（i，j）如果i≠j，且i2－i＋z＝0和j2－j＋z＝0，求k的值。
 |