2006年南京一中初三第一次模拟考试(数学)试卷
一、选择题(每题四个选顶中只有一个是正确的)(每题2分,共24分)
1.-2006的绝对值是
A.-2006 B.![]() C.
C.![]() D.2006
D.2006
2.地球赤道长约为![]() 千米,我国最长的河流——长江全长约为
千米,我国最长的河流——长江全长约为![]() 千米,赤道长
千米,赤道长
约等于长江长的
 A.7倍 B.6倍 C.5倍 D.4倍
A.7倍 B.6倍 C.5倍 D.4倍
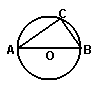
3.如图,AB为⊙O的直径,点C在⊙O上,∠B=50°,则A等于
A.80° B.60° C.50° D.40°
4.下列运算正确的是
A.(-x)2∙x3 =x6
B.![]()
![]()
C.![]() D.
D.![]()
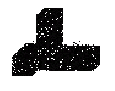 5.右边几何体的俯视图是( )
5.右边几何体的俯视图是( )
6.把分式方程![]() 的两边同时乘以(x-2),约去分母,得
的两边同时乘以(x-2),约去分母,得
A.1-(1-x)=1 B.1+(1-x)=1 C.1-(1-x)= x-2 D.1+(1-x)= x-2
7.方程组 ![]() 的解是
的解是
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
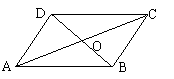 8.如图,□ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是
8.如图,□ABCD中,对角线AC和BD相交于点O,如果AC=12、BD=10、AB=m,那么m的取值范围是
A、1< m <11 B、2< m <22 C、10< m <12 D、5< m <6
9.若M![]() 、N
、N![]() 、P
、P![]() 三点都在函数
三点都在函数![]() (k<0)的图象上,则
(k<0)的图象上,则![]() 的大小关系为
的大小关系为
 A、
A、![]() >
>![]() >
>![]() B、
B、![]() >
>![]() >
>![]() C、
C、![]() >
>![]() >
>![]() D、
D、![]() >
>![]() >
>![]()
10.某学校为了了解学生的课外阅读情况,随机调查了50
名学生,得到他们在某一天各自课外阅读所用时间的
数据,结果如图.根据此条形图估计这一天该校学
生平均课外阅读时为
A.0.96时 B.1.07时 C.1.15时 D.1.50时
11.已知圆柱的底面半径为3,母线长为8,求得这个圆柱的侧面积为
A.24 B.24π C.48 D. 48π
12.在同一平面直角坐标系中,函数y=k(x-1)与y=![]() 的大致图象是
的大致图象是

A. B. C. D.
二、填空题(每题3分,共12分)
13.一个口袋中装有4个白球,1个红球,7个黄球,除颜色外,完全相同,充分搅匀后随机
 摸出一球,恰好是白球的概率是 .
摸出一球,恰好是白球的概率是 .
14.因式分解:![]() = .
= .
15.如图,某学习小组选一名身高为1.6m的同学直立于旗杆影子的顶端处,其他人分为两部分,一部分同学测量该同学的影长为1.2m,另一部分同学测量同一时刻旗杆影长为9m,那么旗杆的高度是______m。
16.已知n(n≥2)个点P1,P2,P3,…,Pn在同一平面内,且其中没有任何三点在同一直线上. 设Sn表示过这n个点中的任意2个点所作的所有直线的条数,显然,S2=1,S3=3,S4=6,S5=10,…,由此推断,Sn=______________.
三、解答题(每题6分,共24分)
17.计算:![]() -
-![]()
18.求不等式组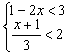 的整数解.
的整数解.
19.化简:![]()
20.如图,梯形ABCD中,AD//BC,AD⊥DC,M为AB的中点.
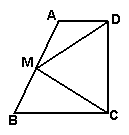 求证:MD=MC.
求证:MD=MC.
四、(每题6分,共12分)
21.在边长为1的5×5的方格中,有一个四边形OABC,
(1)以O点为位似中心,作一个四边形,使得所作四边形与四边形OABC位似,且该四边形的各个顶点都在格点上;
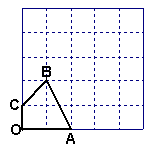 (2)求出你所作的四边形的面积.
(2)求出你所作的四边形的面积.
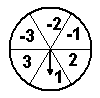
22. 在边长为4的正方形平面内,建立如图所示的平面直角坐标系. 学习小组做如下实验:
连续转动分布均匀的转盘(如图)两次,指针所指的数字作为直角坐标系中P点的坐标(第一次得到的数为横坐标,第二次得到的数为纵坐标).
(1) 转盘转动共能得到 个不同点, P点落在正方形边上的概率是 ;
(2) 求P点落在正方形外部的概率.

五、(每题8分,共16分)
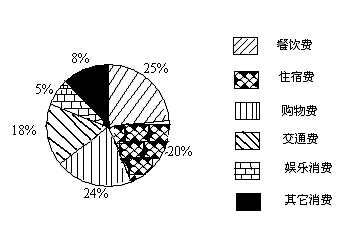
23. 据2006年4月30日我市旅游局预测:今年“五一”黄金周期间,我市实现旅游收入再创历史新高,旅游消费呈现多样化,各项消费所占的比例如图所示,其中住宿消费为5000万元.
(1)求我市今年“五一”黄金周期间旅游消费共多少亿元?旅游消费中各项消费的中位数是多少万元?
(2)对于“五一”黄金周期间的旅游消费,如果我市2008年要达到3.92亿元的目标,那么,2006年到2008年的平均增长率是多少?
2006年我市“五一”黄金周旅游各项消费分布统计图
|
24. 某品牌电热水器,每单位时间内进出水都是一定的,设从某一时刻开始4分钟内只进冷水,不出热水,在随后的8分钟内既进冷水又出热水,如果时间s(分钟)与水量y(升)之间的函数关系如图所示.
(1)每分钟进水多少?
(2)当4≤x≤12时,x与y有何关系?
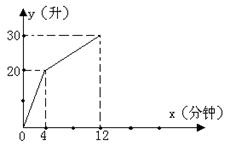 (3)若12分钟后只放热水,不进冷水,求y的表达式,并在图中把相应的图象补充完整.
(3)若12分钟后只放热水,不进冷水,求y的表达式,并在图中把相应的图象补充完整.
六、(每题7分,共14分)
25. 每逢雨季,天降大雨,山体滑坡灾害时有发生,北峰小学教学楼后面紧邻着一个土坡,坡上面是一块平地,如图所示:AF∥BC,斜坡AB长30米,坡角ÐABC=60º。为了防止滑坡,保障安全,学校决定对该土坡进行改造,经过地质人员勘测,当坡角不超过45º时,可以确保山体不滑坡。
(1)求坡顶与地面的距离AD等于多少米?(精确到0.1米)
(2)为确保安全,学校计划改造时保持坡脚B不动,坡顶A沿AF削进到E点处,求AE至少是多少米?(精确到0.1米)

26. 某食品零售店为仪器厂代销一种面包,未售出的面包可退回厂家,经统计销售情况发现,当这种面包的单价定为7角时,每天卖出160个。在此基础上,这种面包的单价每提高1角时,该零售店每天就会少卖出20个.考虑了所有因素后该零售店每个面包的成本是5角。
设这种面包的单价为x(角),零售店每天销售这种面包所获得的利润为y(角)。
⑴求y与x之间的函数关系式;
⑵当面包单价定为多少时,该零售店每天销售这种面包获得的利润最大?最大利润为多少?
七、(本题9分)
27.如图①,正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点,如果两个正方形的边长相等,那么正方形A′B′C′O绕点O无论怎样转动,两个正方形重叠部分的面积总等于一个正方形面积的![]() 。
。
请阅读思考后完成下面三个小题:
(1)若正方形A′B′C′O的边长大于正方形ABCD的边长,正方形ABCD的面积为S,则重叠部分的面积等于 。
(2)若将正方形A′B′C′O改为其它较大的图形,该图形只要满足条件 时,第(1)小题的结论仍然成立。
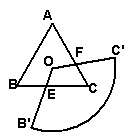
(3)若把正方形ABCD改为正三角形ABC,(如图②),O为正△ABC的中心,以O为顶点的扇形OB′C′绕点O无论怎样转动,要使它与正△ABC的重叠部分的面积总是保持不变,问扇形OB′C′应该满足什么条件?试说明你的理由。

八、(本题9分)
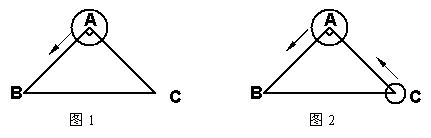
28.如图1,在Rt⊿ABC中,∠A=90o,AB=AC,BC=8![]() ㎝,大圆的圆心在A点,半
㎝,大圆的圆心在A点,半
径为2㎝,大圆以1cm / s的速度移动(圆心从A点出发,沿A—B—C—A方向移动,圆心
始终在Rt⊿ABC边上),设运动时间为t(s).
(1)当大圆与AC边相切时,求t的值;
(2)如果一个小圆的圆心在C点,半径为1㎝,它与大圆同时出发,以2cm / s的速度沿C—A—B—C方向移动,当一个圆的圆心到达其出发点时,另一个圆也停止移动(如图2).
①当两圆相切时,它们的圆心都同时在( )
A. AC边上 B. AB边上 C. BC边上 D. AB和BC边上
 ②当两圆相切时,求t的值.
②当两圆相切时,求t的值.
答案与评分标准:
一、
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| D | B | D | D | C | D | C | A | A | B | D | B |
二、
13.![]() 14.
14.![]() 15.12 16.
15.12 16.![]()
三、17. 原式=![]() -2
-2![]() …… (3分) (每个一分)
…… (3分) (每个一分)
=3-![]() …(6分)
…(6分)
18. -1<x<5,整数解是:0,1,2,3,4.
19. 2 x-4
20. 证法一:延长DA交CB的延长线于E
先证明⊿AMD≌⊿BME,再在直角⊿CDE中利用直角三角形斜边上的中线等于斜边的一半,得到结论.取DC的中点N
证法二:∵M是AB的中点 AD//BC ∴MN//AD
∵AD⊥DC ∴MN⊥DC
∴MN为DC的垂直平分线
∴MD=MC
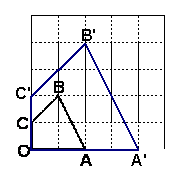 21. (1)如图:
21. (1)如图:
(2)S四边形OA‘B’C‘=10.
22. 列表:
| 1 | 2 | 3 | -1 | -2 | -3 | |
| 1 | (1,1) | (1,2) | (1,3) | (1,-1) | (1,-2) | (1,-3) |
| 2 | (2,1) | (2,2) | (2,3) | (2,-1) | (2,-2) | (2,-3) |
| 3 | (3,1) | (3,2) | (3,3) | (3,-1) | (3,-2) | (3,-3) |
| -1 | (-1,1) | (-1,2) | (-1,3) | (-1,-1) | (-1,-2) | (-1,-3) |
| -2 | (-2,1) | (-2,2) | (-2,3) | (-2,-1) | (-2,-2) | (-2,-3) |
| -3 | (-3,1) | (-3,2) | (-3,3) | (-3,-1) | (-3,-2) | (-3,-3) |
(1)36,![]() ;(2)共有36个点,其中落在正方形外部的点共有20个,概率是:
;(2)共有36个点,其中落在正方形外部的点共有20个,概率是:![]() .
.
23. (1)由图知,住宿消费为5000万元,占旅游消费的25%,
∴旅游消费共5000÷25%=20000(万元)=2(亿元).
交通消费占旅游消费的18%,∴交通消费为20000×18%=3600(万元).
住宿消费占旅游消费的20%,∴住宿消费为20000×20%=4000(万元).
∴今年我市“五一”黄金周旅游消费中各项消费的中位数是
(3600+4000)÷2=3800(万元).
(2)解:设2006年到2008年旅游消费的年平均增长率是![]() ,由题意,得
,由题意,得
2(1+![]() )2=3.92,解得
)2=3.92,解得 ![]() 1=0.4,
1=0.4, ![]() 2=-2.4
2=-2.4
因为增长率不能为负,故![]() 2=-2.4舍去. ∴
2=-2.4舍去. ∴![]() =0.4=40%.
=0.4=40%.
答:2006年到2008年旅游消费的年平均增长率是40%.
24. (1)每分钟进水:![]() (升/分)
(升/分)
(2)由图设![]() ,
,
当x=4时,y=20,∴20=4k+b 当x=12时,y=30,∴30=12k+b
解得:![]() ,
,![]() , ∴当4≤x≤12时,
, ∴当4≤x≤12时,![]()
(3)![]() ,
,![]() ∴
∴![]() (升/分)
(升/分)
∴![]()
25. (1)在Rt△ADB中,AB=30m,ÐABC=60º,sinÐABC=
∴AD=AB·sinÐABC
=30×sin60º
≈26.0(m)
答:AD等于26.0米。
(2)在Rt△ADB中
cosÐABD=
∴DB=AB·cosÐABD
=30×cos60º
=15(m)
连结BE、过E作EN^BC于N
∵AE∥BC
∴四边形AEND为矩形
NE=AD≈26.0
在Rt△ENB中,由已知ÐEBN≤45º
当EBN=45º时
BN=EN=26.0
∴AE=ND=BN-BD=11.0(m)
答:AE至少是11.0 m.
26. (1)y=(x-5)[160-20(x-7)]
即:y=-20x2+400x-1500;
(2)y=-20(x-10)2+500
所以,当面包单价定为10角时,每天销售这种面包获得的利润最大,最大利润为500角.
27. (1)![]() S;(2)∠A′OC′=90°;
S;(2)∠A′OC′=90°;
(3)圆心角∠B′OC′=120°,
证明:连结OB、OC,由∠BOC=∠B′OC′=120°
易证△BOE≌△COF,
∴S四边形OECF=S△BOC=![]() S△ABC
S△ABC
故当∠B′OC′=120°,不论扇形O B′C′怎样转动,重叠部分的面积总等于![]() S△ABC。
S△ABC。
28. (1)t=2s或t=8+6![]() (s);
(s);
(2)① D ② t=5、7、9、11s.