2006年闵行区初三调研测试数学试卷

（100分钟完成，满分150分）

题号	一	二	三	四	总分
得分

考生注意：除第一，二大题外，其余各题都必须写出主要的计算或论证步骤．

一、填空题：（本题共12题，每题3分，满分36分）

1．计算：_______________．

2．不等式的解集是_________________．

3．分解因式：______________________．

4．函数的定义域是______________．

5．如果方程有两个相等的实数根，那么___________．

6．已知：一次函数的图象与直线平行，并且经过点

　 ，那么这个一次函数的解析式是___________________．

7．某校组织初三学生春游，有m名师生租用45座的大客车若干辆，共有4个空座位，那么租用大客车的辆数是____________（用m的代数式表示）．

8．如果直角三角形的两条直角边分别等于5cm和12cm，那么这个直角三角形斜边上的中线长等于_____________cm．

9．在△ABC中，边BC上的中线AD等于9cm，那么这个三角形的重心G

到顶点A的距离是　　　　　  cm．

10．已知梯形的上底和下底的长分别等于5cm、11cm，那么梯形的中位线长等于___________cm．

11．已知D、E分别在△ABC的边AB、AC上，，，

，那么　　　　　  ．

12．已知两圆相切，圆心距等于5cm，两圆的半径之比为2∶3，那么较大的圆的半径等于_______________cm．

二、选择题：（本题共4题，每题4分，满分16分）

【在下列各题的四个备选答案中，只有一个是正确的，请你将正确答案前的字母填在题后的括号内】

13．下列根式中与是同类二次根式的是…………………………（　　 ）

（A）；　 （B）；　　（C）；　 （D）．

14．下列方程中，没有实数根的方程是………………………………（　　 ）

　 （A）；　　　　　（B）；

（C）；　　　　　 　 （D）．

15．在Rt△ABC中，，，，，那么下列等式成立的是……………………………………………………………（　　 ）

（A）；　　　　　 （B）；

（C）；　　　　　　　　　　　　　（D）．

16．下列判断一定正确的是……………………………………………（　　 ）

（A）有两角和其中一角的对边对应相等的两个三角形全等；

（B）有一个角和一边对应相等的两个直角三角形全等；

（C）有两边和其中一边的对角对应相等的两个三角形全等；

（D）有两边对应相等，且有一个角为的两个等腰三角形全等．

三、（本题共5题，第17、18题每题9分，第19、20、21题每题10分，满分48分）

17．计算：．

18．解不等式组：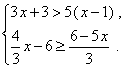

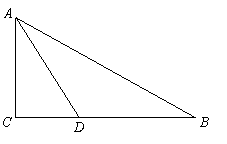19．如图，在Rt△ABC中，，点D在边BC上，，

　  ，求的值．

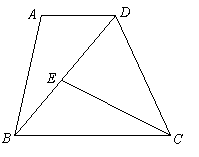
20．如图，在梯形ABCD中，，点E在对角线BD上，

且，如果，CD∶BD = 2∶3，求CE的长．

21．调查我区某校四个年级学生暑假期间所读课外书的情况．学生分布如图（a），读书情况的条形图如图（b），已知该校四个年级共有学生1800人．

（1）该校中预年级学生有________人；

（2）暑假期间读课外书总量最少的是_______年级学生，共读课外

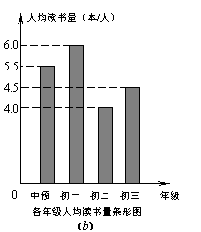书_______________本．

四、（本题共4题，第22、23、24题每题12分，第25题14分，满分50分）

22．如图，AB是⊙O的直径，点P在AB的延长线上，弦，联结OD、PC，，求证：PC是⊙O的切线．

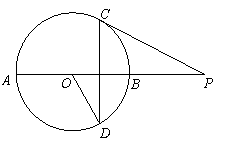23．初中就要毕业了，几位同学准备学业考试结束后结伴去苏州旅游，预计共需费用1200元，后来又有2位同学参加进来，但总的费用不变，于是每人可少分担30元，试求共有几位同学准备结伴去苏州旅游？

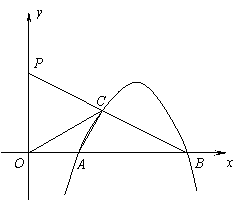24．如图，抛物线与x轴正半轴交于、 两点，且．

（1）求m的值；

（2）抛物线上另有一点C在第一象

限，设BC的延长线交y轴于P．

如果点C是BP的中点，求点C

坐标；

（3）在（2）的条件下，求证：△OCA∽△OBC．

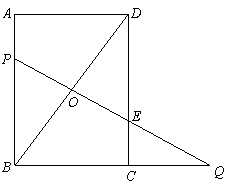
25．如图，在矩形ABCD中，，，O是对角线BD的中点，点P在边AB上，联结PO并延长，交边CD于点E，交边BC的延长线于点Q．

　 （1）求证：；

　 （2）设，，求y与x的函数关系式，并写出自变量x的取值范围；

（3）试判断△CQE能否成为等腰直角三角形，如果能，请求出x的值；如果不能，请说明理由．

2006年闵行区初三调研测试数学试卷

参考答案以及评分建议

一、填空题：（本题共12题，每题3分，满分36分）

1．； 2．； 3．； 4．且； 5．；

6．； 7．； 8．6.5； 9．6； 10．8； 11．9； 12．3或15．

二、选择题：（本题共4题，每题4分，满分16分）

13．D；14．B；15．C；16．A．

三、（本题共5题，第17、18题每题9分，第19、20、21题每题10分，满分48分）

17．解：原式　……………………………3分，3分，3分

．…………………………………………………………1分

18．解：由① 得，…………………………………………………2分

　　　　解得　 ． ……………………………………………………1分

由② 得， …………………………………………………2分

解得　 ． ……………………………………………………2分

所以，原不等式组的解集是． …………………………2分

19．解：在Rt△ADC中，，

由，，解得．………………3分

由勾股定理得 ．所以．………3分

在Rt△ABC中，，

由勾股定理得， ……………2分

所以，． …………………………2分

20．解：在梯形ABCD中，，所以， …………2分

　　　　因为，所以， …………………2分

　　　　又因为，所以△CDE∽△BDC， ………………2分

　　　　所以，……………………………………………………2分

　　　　因为，CD∶BD = 2∶3，所以． …………………2分

21．（1）468；…………4分（2）初三，…………3分．1782．…………3分

四、（本题共4题，第22、23、24题每题12分，第25题14分，满分50分）

22．证明：联结OC，AP与CD交于点E．

　　　　  因为OC、OD是⊙O的半径，所以，………………2分

　　　　  所以． …………………………………………1分

　　　　  因为，所以． ………………………2分

　　　　  因为，所以，……………………………2分

　　　　  所以，…………………………………………1分

　　　　  所以，即．…………………2分

　　　　  因为OC是⊙O的半径，所以PC是⊙O的切线．……………2分

23．解：设共有x位同学准备结伴去苏州旅游． …………………………1分

　　　  根据题意，得，…………………………………5分

　　　  整理后，得　，……………………………………2分

　　　  解得　　　　，（不合题意，舍去）． …………2分

　　　  经检验：是原方程的解，且符合题意．

所以，原方程的解是． ……………………………………1分

　　　  答：共有10位同学准备结伴去苏州旅游．………………………1分

24．解：（1）由题意得，，………………………1分

　　　　　  于是由，解得，，………………………1分

所以，． ……………………………………………1分

（2）由（1）得点B的坐标是，

． …………………………………2分

　　 当点C是BP的中点时，得点C的横坐标是3， …………1分

　　 于是，当时，得． …1分

　　 所以，点C的坐标是．……………………………1分

（3）由（1）得点A的坐标是．…………………………1分

于是，，，．………1分

所以，，……………………………………………1分

又因为，所以△OCA∽△OBC． …………1分

25．（1）证明：在矩形ABCD中，，所以， …1分

　　　　　　  因为O是对角线BD的中点，所以， …………1分

　　　　　　  又因为，所以△BOP≌△DOE， ………1分

　　　　　　  所以． ……………………………………………1分

　 （2）解：因为，，所以． …………………1分

　　　　　  因为△BOP≌△DOE，所以，

　　　　　  于是，由得．………………………………1分

　　　　　  因为，所以， ……………………………1分

　　　　　  即，所以，． …………2分

　 （3）解：当△CQE是等腰直角三角形时，得，

即， …………………………………………………1分

　　　　　  于是由，得，…………………1分

解得，（舍去）． ………………………………1分

所以，当时，△CQE是等腰直角三角形． …………1分