《解直角三角形》知识检测

一、选择题（每小题3分，共24分）

1．在Rt△ABC中，如果一条直角边和斜边的长度都缩小至原来的，那么锐角A的各个三角函数值（　　）

　　A．都缩小　　　　B．都不变　　C．都扩大5倍　　 D．无法确定

2．在△ABC中，∠C＝90⁰，CD是AB边上的高，则CD∶CB等于（　　）

 A．sinA　　　 B．cosA　　  C．tanA　　　　D．cotA

3．A、B、C是△ABC的三个内角，则等于（　　）

 A．　　 B．　　 C．　　 D．

4．若0⁰＜A＜90⁰，且，则的值为（　　）

 A．5　　　　 B．　　  C．　　　 D．

5．在Rt△ABC中，∠C＝90⁰，，则∶∶为（　 ）

A．2∶∶ B．2∶∶3　C．2∶3∶ D．1∶2∶3

6．如图1，△ABC中，∠ACB=90°，以△ABC的各边为边在△ABC外作三个正方形，S₁、S₂、S₃分别表示着三个正方形的面积，S₁=81，S₃=225，则S₂等于（　　）

A．144　 B．100　 C．98　　 D．36

7．两建筑物的水平距离为a米，从较高建筑物AB的顶端A点测得较低建筑物CD底端D点的俯角为β，测得C点的俯角为α,则CD的高为（　　 ）

A．a米　B．atanα米　 C．acotα米　D．a（tanβ-tanα）米

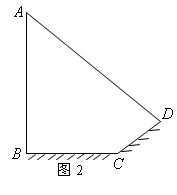
8．如图2，小阳发现电线杆AB的影子落在土坡的坡面CD和地面BC上，量得CD=8米，BC=20米，CD与地面成30º角，且此时测得1米杆的影长为2米，则电线杆的高度为(　　)

A．9米　　B．28米　　C．米　　D．米

二、填空题（每小题4分，共32分）

1．旗杆的上一段BC被风吹断，顶端着地与地面成30⁰角，顶端着地处B与旗杆底端相距4米，则原旗杆高为_________米．

2．在坡度为1:2的斜坡上，某人前进了100米，则他所在的位置比原来升高了　　　 米．

3．计算：＝　　　　  ．

4．已知△ABC中，AB＝，∠B＝45⁰，∠C＝60⁰，AH⊥BC于H，则AH＝　　　；CH＝　　　　　  ．

5．如图3，矩形ABCD（AD＞AB）中，AB=a，∠BDA=α，AE=AB，则用a与α表示：AD=________，BE=__________．

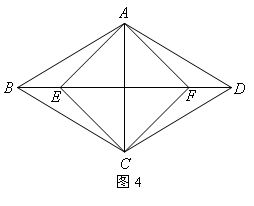6．如图4，菱形ABCD中，点E、F在对角线BD上，BE=DF=BD，若四边形AECF为正方形，则tan∠ABE=_________．

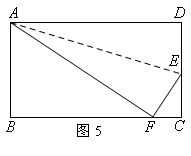
7． 如图5，折叠长方形的一边AD，点D落在BC边的点F处，已知AB=8厘米，BC=10厘米，则EC的长为_________．

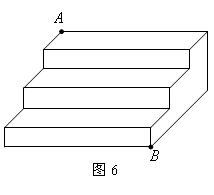
8． 如图6所示是一个三级台阶，它的每一级的长、宽、高分别等于55、10和6，A和B是这个台阶的两个相对的端点，A点上有一只蚂蚁，想到B点去吃可口的食物，则这只蚂蚁从A点出发沿着台阶爬到B点的最短路线的长是__________．

三、计算下列各题：（共64分）

1．（6分）计算：　　　　　　　　　　　　　

2．（8分）在△ABC中，∠C=90⁰，∠B＝30⁰，AD是∠BAC的平分线，已知AB＝，求AD的长．

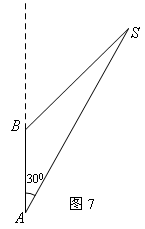3．（8分）一艘船以30海里/时的速度向正北航行，在A处看灯塔S在船北偏东30⁰，半小时后航行到B处，看灯塔S在船的东北方向，求灯塔S和B处的距离．

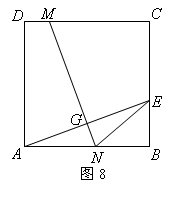4．（10分）如图8，ABCD为正方形，E为BC上一点，将正方形折叠，使A点与E点重合，折痕为MN，若，DC+CE=10．

（1）求△ANE的面积；

（2）求sin∠ENB的值．

5．（10分）同学们对公园的滑梯很熟悉吧？如图9，是某公园新增设的一台滑梯，该滑梯高度AC＝2米，滑梯着地点B与梯架之间的距离BC＝4米．

（1）求滑梯AB的长（精确到0.1米）；

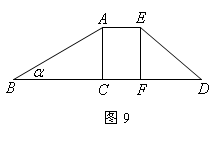（2）若规定滑梯的倾斜角（∠ABC）不超过45⁰，属于安全．通过计算说明这架滑梯的倾斜角是否符合要求？

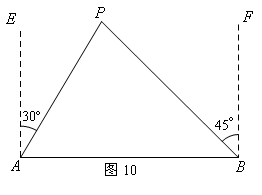
6．（10分）如图10，A、B两座城市相距100千米，现计划在这两城市之间修筑一条高速公路（即线段AB）．经测量，森林保护区中心P点在A城市的北偏东30⁰方向，B城市的北偏西45⁰方向上，已知森林保护区的范围在以P为圆心，50千米为半径的圆形区域内．

请问：计划修建的这条高速公路会不会穿越保护区，为什么？

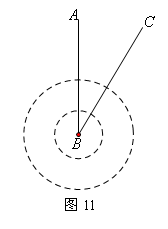7．（12分）台风是一种自然灾害，它以台风中心为圆心在周围数十千米范围内形成气旋风暴，有极强的破坏力，如图11，据气象观测，距沿海某城市A的正南方向220千米B处有一台风中心，其中心最大风力为12级，每远离台风中心20千米，风力就会减弱一级，该台风中心现在以15千米／时的速度沿北偏东30⁰方向往C移动，且台风中心风力不变，若城市所受风力达到或超过四级，则称为受台风影响．

（1）该城市是否会受到这次台风的影响？请说明理由．

（2）若会受到台风影响，那么台风影响该城市的持续时间有多长？

（3）该城市受到台风影响的最大风力为几级？

答案与提示

一、选择题

BBAB BADD

二、填空题

1、；2、；3、；4、4，；5、acotα，2asinα；6、；7、3；8、73

三、解答题

1、；2、AD=＝4

3、过S作SC⊥AB的延长线于C，设SB=x，解得x＝．

4、设BE＝x，则AB=3x，则5x＝10，解得x＝2，从而EB=2，AB=6；设AN=y，则EN＝y，BN＝6-y，由勾股定理解得y＝ ∴S_△ANE=，sin∠ENB=．

5、（1）4.5米；（2）∠ABC≈27⁰＜45⁰，故符合要求．

6、过P作PC⊥AB，设PC＝x，则AC=x，BC=PC=x，解得x≈63.4＞50，故不会穿过保护区．

7、（1）由点A作AD⊥BC，由题意，当A点距台风中心不超过160千米时，将会受到台风的影响，由于AD=110<160,所以A市会受到这次台风的影响；（2）在BD及BD的延长线上分别取E、F两点，使AE=AF=160千米。由勾股定理,得DE=30  求得这次台风影响该城市的持续时间小时； (3)当台风中心位于D处时,A市所受这次台风的风力最大，其最大风力为6.5级．