2006年广东省从化市九年级数学第一次综合测试
数学试卷
(考试时间120分钟,满分150分)
第I卷(选择题 共30分)
一、选择题(每小题3分,计30分,下列各小题都给出了四个选项,其中只有一项是符合题目要求的,请将符合要求的选项前面的字母代号填写在第II卷上指定的位置.)
1.![]() 的值是
的值是
A 、-3 B、-2 C、7 D、3
2.化简![]() 的结果是 .
的结果是 .
A、 4 B、![]() C、 2.
D、
C、 2.
D、![]()
3.下图中①表示的是组合在一起的模块,在甲、乙、丙、丁四个图形中,是这个模块的俯视图的是
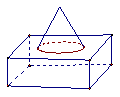
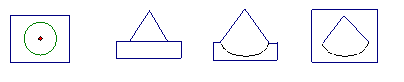
① 甲 乙 丙 丁
A、甲 B、乙 C、丙 D、丁
4.下列调查中,可以采用普查方式进行调查的是
A、电视机厂要了解一批显像管的使用寿命。
B、要了解从化市居民的环保意识。
C、要了解从化“荔枝的甜度和含水量”。
D、要了解你校数学教师的年龄状况。
 5.下列图形都由几个部分组成,可以只用其中一部分平移就可以得到的图是
5.下列图形都由几个部分组成,可以只用其中一部分平移就可以得到的图是
 | 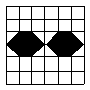 | ||||
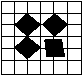 | |||||
A B C D
6. 下列命题中,正确的是
A. 两条直线同时与第三条直线相交,则同位角相等
B. 平行四边形的对角线互相垂直平分
C. 等腰梯形的对角线互相垂直 D. 矩形的对角线互相平分且相等
7. 若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6,4!=4×3×2×1,…,则7![]() 6!的值为
6!的值为
 A. 42! B.
7! C.
6
A. 42! B.
7! C.
6![]() 7! D.
6
7! D.
6![]() 7!
7!
8. 如右图,若A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,为使△ABC∽△PQR,则点R应是甲、乙、丙、丁四点中的
A. 甲 B. 乙
C. 丙 D. 丁
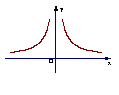 9.如右图所示的函数图象的关系式可能是
9.如右图所示的函数图象的关系式可能是
A . y = x B. y =![]() C. y =
x2 D. y =
C. y =
x2 D. y = ![]()
10.若半径为1cm和2cm的两圆相外切,那么与这两个圆都相切且半径为3cm的圆的个数是:
A. 5个 B. 4个 C. 3个 D.2个
第II卷 (共120分)
二、填空题(本大题共6个小题,每小题3分,共18分)
11.计算:![]() =__________________ .
=__________________ .
12.若实数![]() 满足条件
满足条件![]() ,试写出一个
,试写出一个![]() 和一个
和一个![]() 使它们满足这个条件,此时
使它们满足这个条件,此时
![]() =
;
=
;![]() =
.
=
.
13.在直角![]() ABC中,
ABC中,![]() C=900,若AB=5,AC=4,则cos
C=900,若AB=5,AC=4,则cos![]() B的值是
.
B的值是
.
14.已知公式:![]() 可用来进行因式分解,其中
可用来进行因式分解,其中![]() 是方程
是方程![]() 的两根,试分解因式:2
的两根,试分解因式:2![]() =________________ _ .
=________________ _ .
15.从50张分别写上1~50的数字卡中,随意抽取一张是8的倍数的概率为 .
16.小军的期末总评成绩由平时、期中、期末成绩按权重比1:1:8 组成,现小军平时考试得90分,期中考试得60分,要使他的总评成绩不低于79分,那么小军的期末考试成绩![]() 满足的条件是
.
满足的条件是
.
三、解答题(本大题共9个小题,共102分)
17.(本小题8分)
解方程:![]()
18. (本小题9分)
解不等式组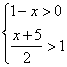
19. (本小题9分)
计算:![]()
20. (本小题10分)
下表是从化市2004年街口街居民收支情况抽样调查表,阅读表内信息,完成下列问题:
| 项目 | 2004年(元) | 2003年(元) | 同比增长(%) | |
| 可支配收入 | 工薪收入 | 8077.85 | 6349.41 | 27.2 |
| 经营性收入 | 289.77 | 222.53 | 30.2 | |
| 财产性收入 | 110.92 | 59.93 | 85.1 | |
| 转移性收入 | 3118.97 | 3353.76 | -7.0 | |
| 小计 | 11597.51 | 9985.63 |
| |
| 消费支出 | 食品 | 3595.12 | 3060.34 | 17.5 |
| 衣着 | 800.72 | 699.14 | 14.5 | |
| 家庭设备用品及服务 | 484.00 | 419.95 | 15.3 | |
| 医疗保健 | 715.17 | 689.22 | 3.8 | |
| 交通和通讯 | 936.31 | 708.32 | 32.2 | |
| 教育文化娱乐服务 | 1099.44 | 1094.92 | 0.4 | |
| 居住 | 623.13 | 732.98 | -15.0 | |
| 杂项商品和服务 | 417.87 | 355.03 | 17.7 | |
| 小计 | 8671.76 | 7759.90 |
| |
(1)说明街口街居民可支配收入的主要来源是什么收入.
(2)街口街居民可支配收入中同比增长最快的是哪项收入?
(3)从街口街居民在消费支出方面的信息,你能得出哪些结论?试写出其中的两条.
21. (本小题12分)
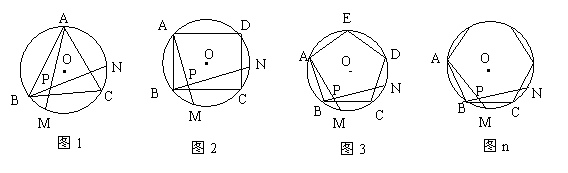
如图,图1、图2、图3、…、图n分别是⊙O的内接正三角形ABC,正四边形ABCD、正五边形ABCDE、…、正n边形ABCD…,点M、N分别从点B、C开始以相同的速度在⊙O上逆时针运动。
(1)求图图1中∠APN的度数是 ;图2中,∠APN的度数是_______,
图3中∠APN的度数是________.
(2)试探索∠APN的度数与正多边形边数n的关系(直接写答案)
 |
22. (本小题12分)
一对骰子,如果掷两骰子正面点数和为2、11、12,那么甲赢;如果两骰子正面的点数和为7,那么乙赢;如果两骰子正面的点数和为其它数,那么甲乙都不赢。继续下去,直到有一个人赢为止.
(1)你认为游戏是否公平,并解释原因.
(2)如果你认为游戏公平,那么请你设计一个不公平的游戏;如果你认为游戏不公平,那么请你设计一个公平的游戏.
23. (本小题12分)
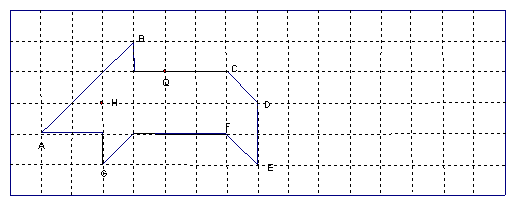
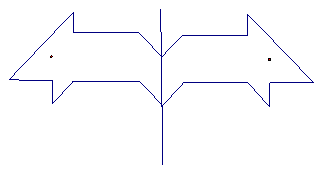
下面的方格纸中,画出了一个“小老鼠”的图案,已知每个小正方形的边长为1
(1)在上面的方格纸中作出“小老鼠”关于直线DE对称的图案(只画图,不写作法).
(2)以G为原点,GE所在直线为x轴,GH所在直线为y轴,小正方形的边长为单位长度建立直角坐标系,问:是否存在以点Q 为顶点,且过点H和E的抛物线,并通过计算说明理由?
24. (本小题15分)
如图,梯形ABCD中,AD∥BC,AB=DC,∠ADC=120°,对角线CA平分∠DCB,E为BC的中点.
 (1)试判断四边形ABED的形状,并进行证明.
(1)试判断四边形ABED的形状,并进行证明.
(2)试求![]() DCA与梯形ABEP的面积之比.
DCA与梯形ABEP的面积之比.
25. (本小题15分)
如图,在正方形ABCD中,AB=![]() ,E是AD边上的一点(点E与点A和点D不重合),BE的垂直平分线交AB于点M,交DC于点N.
,E是AD边上的一点(点E与点A和点D不重合),BE的垂直平分线交AB于点M,交DC于点N.
(1)证明:MN = BE.
(2)设AE=![]() ,四边形ADNM的面积为S,写出S关于
,四边形ADNM的面积为S,写出S关于![]() 的函数关系式.
的函数关系式.
(3)当AE为何值时,四边形ADNM的面积最大?最大值是多少?

2006年从化市九年级数学第一次综合测试
数学参考答案
一、选择题:每小题3分,共30分;
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 选项 | A | B | A | D | B | D | B | C | D | A |
二、填空题:每小题3分,共18分;
11、 1 ; 12、 1 ; 1 (答案不唯一第一空2分,第二空1分);
13、![]() ;
14、
;
14、![]() 或
或![]()
15、![]() ;
16、
;
16、![]() (无等号不给分);
(无等号不给分);
三、解答题:
17题:
解:由方程 ![]()
去分母得:![]() ………………………………………2
………………………………………2
去括号得:![]() …………………………………………4
…………………………………………4
移项得:![]()
得:![]() …………………………………………………………………… 6
…………………………………………………………………… 6
经检验是![]() 原方程的根。……………………………………….……………8
原方程的根。……………………………………….……………8
18题:
解:由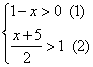
解不等式(1)得到:![]() ……………………………………………………………..3
……………………………………………………………..3
解不等式(2)得到:![]() …………………………………………………………….6
…………………………………………………………….6
由不等式(1)和(2)得到:![]() ……………………………………………….9
……………………………………………….9
19题:
解: ![]()
=![]() (对三个分子与分母及除号的处理,每部分给2分)…………..8
(对三个分子与分母及除号的处理,每部分给2分)…………..8
=![]() ……………………………………………………………………………………....9
……………………………………………………………………………………....9
20题:
解:(1)工薪收入; ………………………………………………………………..3
(2)财产性收入;………………………………………………………………..6
(3)主要消费支出是食品; 消费支出中只有居住消费在减少;………….10
21题:
解:(1)600 ;900 ;1080
;(每空2分,共6分) (2)![]() ;(6分)
;(6分)
22题:
解:(1)不公平;………………………………………………………….2
因为甲掷出两骰子点数为2、11、12的情况分别为:1+1,5+6,6+5,6+6;
……………………………………………….….4
而乙掷出两骰子点籾之和为7的情况分别是:1+6,6+1,3+4,4+3,2+5,5+2;
……………………………………………………6
所以甲赢的概率是![]() ,乙赢的概率是
,乙赢的概率是![]() ;偏向乙;……………..8
;偏向乙;……………..8
(2)若点数为6,则甲赢,若点数和为5或2,则乙赢;………..12
 23题:
23题:
解:(1)如下图:…………………..4
(若漏掉眼睛所在的点扣一分,
每错一处扣1分,扣完4分为止)
(2)建立坐标系后:
它们的坐标分别是:
H(0,2), Q(2,3), E(5,0)………..7
假设存在这样的抛物线:
设函数式为:![]() …………………..8
…………………..8
因为H在抛物线上,所以把![]()
代入抛物线![]()
![]()
所以函数表达式是:![]() ……………………10
……………………10
若点E在抛物线上,则x = 5时,y = 0 ;
把x=5, 代入抛物线有:![]()
所以点E不在抛物线上。……………………………..……11
所以不存在以点Q为顶点,同时又经过点H和点E的抛物线。……………12
 24、(1)四边形ABED是菱形;
24、(1)四边形ABED是菱形;
证明:![]()
![]()
![]() ………..…..1分;
………..…..1分;
又![]() CA平分
CA平分![]()
![]() ;
;
又AD//BC;
![]()
![]() ……………………………3
……………………………3
又![]()
![]()
在直角三角形ABC中,![]() ;……………………..5
;……………………..5
![]()
![]()
所以四边形ABED是菱形。…………………………………7
(2)设梯形的高是H
![]() ;………………………….10
;………………………….10
又![]() ;………………………..13
;………………………..13
![]() ………………………………………………….15
………………………………………………….15
25、
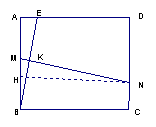 解:(1)证明:
解:(1)证明:
作NH![]() AB,交AB于H,………………………….1
AB,交AB于H,………………………….1
则HN![]()
![]() …………………………………………….2
…………………………………………….2
又![]() ,设交点为K,
,设交点为K,
![]()
又由![]() ,
,
四边形的内角和为3600 ,
![]()
由(1),(2)得到:![]() ……………………4
……………………4
在![]() 和
和![]() 中
中
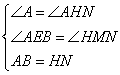
![]()
![]() …………………………………………………..7
…………………………………………………..7
(2)由![]() 得到 :
得到 :
![]() ………………………………………………………. 8
………………………………………………………. 8
所以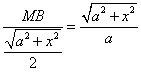
………………………………………………………………………………………………….10
所以:![]() ,
,![]() ,
,![]()
所以![]() , ……………………………………..11
, ……………………………………..11
(3) 由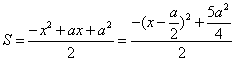 ……………………………………………13
……………………………………………13
当![]() 时,
时,![]()
![]() 时 ,
时 ,![]() ……………………………………………………………15
……………………………………………………………15
