1.3~1.5 三角函数的有关计算、船有触礁的危险吗、测量物体的高度(A卷)
(50分钟,共100分)
班级:_______ 姓名:_______ 得分:_______ 发展性评语:_____________
一、请准确填空(每小题3分,共24分)
1.Rt△ABC中,∠C=90°,AB=8,sinA=![]() ,则AC=______.
,则AC=______.
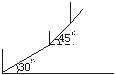
图1
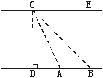
2.小刚在一山坡上依次插了三根木杆,第一根木杆与第二根木杆插在倾斜角为30°,且坡面距离是6米的坡面上,而第二根与第三根又在倾斜角为45°,且坡面距离是8米的坡面上.则第一根与第三根木杆的水平距离是______.(如图1)(精确到0.01米)
3.在△ABC中,∠C=90°,已知BC=m,∠A=α,则∠B=_____,AC=_____,AB=_____.
4.菱形的两条对角线长分别为2![]() 和6,则菱形的相邻的两内角分别为______.
和6,则菱形的相邻的两内角分别为______.
5.等腰三角形腰上的高等于底上的高的一半,则底角的余弦值为______.
6.△ABC中,∠ACB=90°,CD⊥AB于点D,AD、DB的长是方程x2-20x+m=0的根,若△ABC的面积为40,则m=______.
7.某人在20米高的塔顶测得地面上的一点的俯角是60°,这点到塔底部的距离约为______.(精确到0.1米)
8.升国旗时,某同学站在离旗杆底部24米处行注目礼,当国旗升至旗杆顶端时,该同学视线的仰角恰为30°,若双眼离地面1.5米,则旗杆的高度为______米.(用含根号的式子表示)
二、相信你的选择(每小题3分,共24分)
9.如图2,四边形ABCD中,∠A=135°,∠B=∠D=90°,BC=2![]() ,AD=2,则四边形ABCD的面积是
,AD=2,则四边形ABCD的面积是
A.4![]() B.4
B.4![]() C.4 D.6
C.4 D.6
图2
10.如果坡角的余弦值为![]() ,那么坡度为
,那么坡度为
A.1∶![]() B.3∶
B.3∶![]() C.1∶3 D.3∶1
C.1∶3 D.3∶1
11.等腰三角形的三边的长分别为1、1、![]() ,那么它的底角为
,那么它的底角为
A.15° B.30° C.45° D.60°
12.身高相同的三个小朋友甲、乙、丙放风筝,他们放出的线长分别为300 m,250 m,200 m;线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放的风筝
A.甲的最高 B.乙的最低 C.丙的最低 D.乙的最高
13.如图3,为了测量一河岸相对两电线杆A、B间的距离,在距A点15米的C处 (AC⊥AB)测得∠ACB=50°,则A、B间的距离应为
A.15sin50°米 B.15tan50°米
C.15tan40°米 D.15cos50°米
14.△ABC中,∠A=60°,AB=6 cm,AC=4 cm,则△ABC的面积是
A.2![]() cm2
B.4
cm2
B.4![]() cm2
cm2
C.6![]() cm2
D.12 cm2
cm2
D.12 cm2
15.如图4,在离地面高度5 m处引拉线固定电线杆,拉线和地面成60°角,则拉线AC的长是
A.10 m
B.![]() m
C.
m
C.![]() m D.5
m D.5![]() m
m

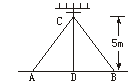

图3 图4 图5
16.如图5,小红从A地向北偏东30°的方向走100米到B地,再从B地向正西走200米到C地,这时小红距A地
A.150米
B.100![]() 米
C.100米
D.50
米
C.100米
D.50![]() 米
米
三、考查你的基本功(共20分)
17.(10分)如图6,在Rt△ABC中,∠C=90°,AC=8,∠A的平分线AD=![]() 求
∠B的度数及边BC、AB的长.
求
∠B的度数及边BC、AB的长.
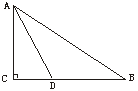
图6
18.(10分)等腰三角形的底边长20 cm,面积为![]() cm2,求它的各内角.
cm2,求它的各内角.
四、生活中的数学(共21分)
19.(10分)下表是小亮同学填写实习报告的部分内容:
| 题 目 | 在两岸近似平行的河段上测量河宽 |
| 测量目标图示 |
|
| 测得数据 | AB=15米,∠DBC=45°,∠ACB=15°,∠BDC=90° |
请根据以上的条件,计算出河宽CD.(结果精确到0.1米)
20.(11分)某地区为提高某段海堤的防海潮能力,计划将长96 m的一堤段(原海堤的横断面如图7中的梯形ABCD)的堤面加宽1.6 m,背水坡度由原来的1∶1改成1∶2,已知原背水坡长AD=8.0 m,求完成这一工程所需的土方,要求保留两个有效数字.(提供数据![]() ≈1.414,
≈1.414,![]() ≈1.73,
≈1.73,![]() ≈2.24)
≈2.24)

图7
五、探究拓展与应用(共11分)
21.(11分)在一座高为10 m的大楼顶C测得旗杆底部B的俯角α为60°,旗杆顶端A的仰角β为20°.(![]() 取1.73,tan20°≈0.3646)
取1.73,tan20°≈0.3646)
(1)求建筑物与旗杆的水平距离BD;
(2)计算旗杆高.(精确到0.1 m)
图8
参考答案
一、1.2![]() 2.10.85 3.90-α
2.10.85 3.90-α ![]() 或mcotα
或mcotα ![]() 4.60°、120° 5.
4.60°、120° 5.![]() 6. 16 7.
6. 16 7.![]() ≈11.5(米) 8.(8
≈11.5(米) 8.(8![]() +1.5)米
+1.5)米
二、9.C 10.C 11.B 12.D 13.B 14.C 15.B 16.B
三、17.在Rt△ACD中
∵cosCAD=![]() =
=![]() =
=![]() ,∠CAD为锐角.
,∠CAD为锐角.
∴∠CAD=30°,∠BAD=∠CAD=30°,
即∠CAB=60°.
∴∠B=90°-∠CAB=30°.
∵sinB=![]() ,∴AB=
,∴AB=![]() =
=![]() =16.
=16.
又∵cosB=![]() ,
,
∴BC=AB·cosB=16·![]() =8
=8![]() .
.
18.解:设等腰三角形底边上的高为x cm,底角为α,则有![]() x·20=
x·20=![]() ,
,
∴x=![]() .
.
∵tanα =![]() =
=![]() ,∴∠α=30°.
,∴∠α=30°.
顶角为180°-2×30°=120°.
∴该等腰三角形三个内角为30°,30°,120°.
四、19.CD≈35.5(米).
20.解:分别作DM⊥AB交AB于M,EN⊥AB交AB于N.
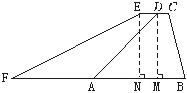
∵![]() =
=![]() ,∴∠DAM=45°.
,∴∠DAM=45°.
∵AD=8,∴DM=AM=4![]() .
.
又∵CD∥AB,∴EN=DM=4![]() ,
,
DE=MN=1.6.
在Rt△FNE中,![]() =
=![]() ,
,
∴FN=2EN=8![]() .
.
∴FA=FN+NM-AM=8![]() +1.6-4
+1.6-4![]() =4
=4![]() +1.6≈7.26.
+1.6≈7.26.
S四边形ADEF=![]() (AF+DE)·EN=
(AF+DE)·EN=![]() (7.26+1.6)×5.66≈25.07(m2).
(7.26+1.6)×5.66≈25.07(m2).
V体积=S四边形ADEF×96=25.07×96=2.4×103(m3).
答:完成这一工程需2.4×103 m3的土方.
五、21.解:(1)∵∠CBD=α=60°,
∴在Rt△BDC中,
tanCBD=![]() .
.
∴BD=![]() =
=![]() =
=![]() (m).
(m).
(2)设CE⊥AB,垂足为E,
∴CE=BD=![]() (m).
(m).
在Rt△AEC中,
∵tanβ=![]() ,
,
∴AE=CE·tanβ=![]() ·tan20°≈2.1(m).
·tan20°≈2.1(m).
∴AB=2.1+10=12.1(m),即旗杆高为12.1 m.