1.3~1.5 三角函数的有关计算、船有触礁的危险吗、测量物体的高度(B卷)
(50分钟,共100分)
班级:_______ 姓名:_______ 得分:_______ 发展性评语:_____________
一、请准确填空(每小题3分,共24分)
1.如图1,从楼顶A点测得电视塔CD的仰角为α,俯角为β,若楼房与电视塔之间的水平距离为m,求电视塔的高度.将这个实际问题写成数学形式:已知在△ADC中,AB_____CD于B,∠_____=α,∠_____=β,m=_____,求_____.
2.如图2,水库大坝的横断面是梯形,坝顶宽5 m,坝高20 m,斜坡AB的坡度为1∶2.5,斜坡CD的坡度为1∶2,则坝底宽AD等于______.
3.某段公路每前进100 m,就升高4 m,则路面的坡度约为_____.
4.如果由点A测得点B在北偏西20°的方向,那么由点B测得点A的方向是______.
5.某展厅为迎接科技展览,准备在大厅的主楼梯上铺设某种红色地毯,已知这种地毯每平方米售价30元,主楼梯道宽2 m,其侧面如图3所示,则购买地毯至少需要______元.



图1 图2 图3
6.△ABC中,∠C=90°,斜边上的中线CD=6,sinA=![]() ,则S△ABC=______.
,则S△ABC=______.
7.如图4小明想测量电线杆AB的高度,发现电线杆的影子恰好落在土坡的坡面CD和地面BC上,量得CD=4 m,BC=10 m,CD与地面成30°角,且此时测得1 m杆的影子长为2 m,则电线杆的高度约为_____m.(结果保留两位有效数字,![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
8.把一条长1.35 m的铁丝弯成顶角为120°的等腰三角形,则此等腰三角形底边长为______.(精确到0.1 m)
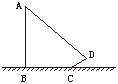

图4 图5
二、相信你的选择(每小题4分,共32分)
9.在△ABC中,已知AC=3,BC=4,AB=5,那么下列结论成立的是
A.sinA=![]() B.cosA=
B.cosA=![]() C.tanA=
C.tanA=![]() D.sinB=
D.sinB=![]()
10.已知如图5,小明在打网球时,要使球恰好能打过网,而且落在离网5 m的位置上,则球拍击球的高度h应为
A.2.7 m B.1.8 m C.0.9 m D.6 m
11.如果α是锐角,且cosα=![]() ,那么cos(90°-α)的值是
,那么cos(90°-α)的值是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.如图6,在△ABC中,点D在AC上,DE⊥BC,垂足为E,若AD=2DC,AB=4DE,则sinB等于
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13.如图7,某地夏季中午,当太阳移至房顶上方偏南时,光线与地面成80°角,房屋朝南的窗子高AB=1.8 m,要在窗子外面上方安装水平挡光板AC,使午间光线不能直接射入室内,那么挡光板的宽度AC为
A.1.8tan80°m B.1.8cos80°m
C.![]() m D.
m D.![]() m
m
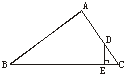
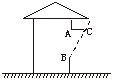
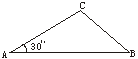
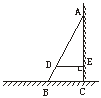
图6 图7 图8 图9
14.如果∠A为锐角,且cosA=![]() ,那么∠A的范围是
,那么∠A的范围是
A.0°<∠A≤30° B.30°<∠A<45°
C.45°<∠A<60° D.60°<∠A<90°
15.如图8,在△ABC中,AB=3,AC=2,∠A=30°,则△ABC的面积等于
A.![]() B.
B.![]() C.
C.![]() D.3
D.3![]()
16.如图9,小红把梯子AB斜靠在墙壁上,梯脚B距墙1.6米,小红上了两节梯子到D点,此D点距墙1.4米,BD长0.55米,则梯子的长为
A.4.50米 B.4.40米 C.4.00米 D.3.85米
三、考查你的基本功(共14分)
17.(10分)阿雄有一块如图10所示的四边形空地,求此空地的面积.(结果精确到0.01 m2,![]() 取1.732)
取1.732)

图10
18.(4分)计算:sin230°+2sin60°+tan45°-tan60°+cos230°.
四、生活中的数学(共20分)
19.(10分)如图11,某国侦察机B飞抵我国近海搞侦察活动,我战斗机A奋起拦截,地面雷达测得:当两机都处在雷达的正东方向的上空并在同一高度时,测得它们仰角分别为 ∠DCA=16°,∠DCB=15°,它们与雷达的距离分别为AC=80千米,BC=81千米,求此时两机距离是多少千米?(精确到0.01 km,cos15°≈0.97,cos16°≈0.96)
![]()
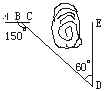
图11 图12
20.(10分)在某高速公路建设中,要沿AC方向开山修路,为加快施工进度,要在山坡 的另一边同时施工.如图12所示,从AC上的一点B量取∠ABD=150°,BD=420 m, ∠D=60°,那么开挖点E离D多远正好使A、C、E成一直线?
五、探究拓展与应用(共10分)
21.(10分)利用老师的教学用具:三角板、量角器、米尺,请你设计一个测量校园旗杆高度的方案,并画出图形,与同伴交流.
参考答案
一、1.⊥ BAC BAD AB CD 2.95
3.1∶24.98 4.南偏东20° 5.504 6.16![]() 7.8.7 8.0.6 m
7.8.7 8.0.6 m
二、9.B 10.A 11.B 12.D 13.D 14.D 15.B 16.B
三、17.如下图,连接BD,
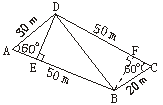
作DE⊥AB于E,
作BF⊥CD于F.
∵∠A=∠C=60°,
∴DE=30·sin60°=15![]() ≈25.98,
≈25.98,
BF=20·sin60°=10![]() ≈17.32.
≈17.32.
S四边形ABCD=S△ABD+S△DBC
=![]() AB·DE+
AB·DE+![]() CD·BF
CD·BF
=![]() ×50×25.98+
×50×25.98+![]() ×50×17.32≈1082.5(m2).
×50×17.32≈1082.5(m2).
18. 2
四、19.解:作AE⊥CD于E,BF⊥CD于F,
则AE∥BF.
在Rt△ACE中,∵cos16°=![]() ,
,
∴CE=80·cos16°≈80×0.96=76.80.
在Rt△BCF中,∵cos15°=![]() .
.
∴CF=81·cos15°≈81×0.97=78.57.
由题意知AB∥CD.
∴AB=EF=CF-CE=78.57-76.80=1.77(千米).
答:此时两机相距1.77千米.
20.解:延长BC交DE于点E.
∵∠ABD=150°,
∴∠CBD=180°-150°=30°.
又∵∠D=60°,
∴∠CED=180°-60°-30°=90°.
在Rt△BDE中,∵sin30°=![]() ,
,
∴DE=BD·sin30°=420×![]() =210(m).
=210(m).
答:在离D 210米的E处开挖,能正好使A、C、E成一直线.
五、21.参考:
方案1:如图(1).
方案2:如图(2).
方案3:如图(3).
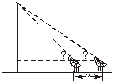


(1) (2) (3)
