1.1~1.2　从梯子的倾斜程度谈起、30°，45°，60°角的三角函数值(B卷)

(50分钟，共100分)

班级：_______　　姓名：_______　　得分：_______　　发展性评语：_____________

一、请准确填空(每小题3分，共24分)

1.如图1，在平面直角坐标系中，P是∠α的边OA上一点，且P点坐标为(4，3)则　　　 sinα=______，cosα=______.

2.已知α是锐角，且2cosα=1，则α=______；若tan(α+15°)=1，则tanα=______.

3.如图2，B、C是河岸边两点，A是对岸岸边一点，测得∠ABC=45°，∠ACB=45°，BC=60 m，则点A到对岸BC的距离是_____m.

　　　　　　 　　　　　　　　

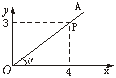
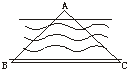
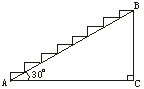
图1　　　　　　　　　　　　　　　　　　　　　　　　　　　　图2　　　　　　　　　　　　　　　　　　　　　　　　 　　  图3

4.要把5米长的梯子上端放在距地面3米高的阳台边沿上，猜想一下梯子摆放坡度最小为______.

5.已知tanα·tan30°=1，且α为锐角，则α=______.

6.设β为锐角，且x²+2x+sinβ=0的两根之差为，则β=______.

7.在△ABC中，∠C=90°.若3AC=BC，则∠A的度数是______，cosB的值是______.

8.如图3，某建筑物BC直立于水平地面，AC=9米，要建造阶梯AB，使每阶高不超过20 cm，则此阶梯最少要建_____阶.(最后一阶的高度不足20 cm时，按一阶算，取1.732)

二、相信你的选择(每小题3分，共24分)

9.在△ABC中，AB=AC=4，BC=2，则4cosB等于

A.1　　　　　　　　　　　 　 B.2　　　　　　　　　　　　 C.　　　　　　　　　　　 D.

 10.△ABC中，∠A、∠B都是锐角，且sinA=，cosB=，则△ABC的形状是

A.直角三角形　　　　　　　　　　　　　　　　　　　 B.钝角三角形

C.锐角三角形　　　　　　　　　　　　　　　　　　　　　  D.不能确定

11.令a=sin60°，b=cos45°，c=tan30°，则它们之间的大小关系是

A.c<b<a　　　　  　　　　　　　　　　　　　　　　 B.b<c<a

C.b<a<c　　　　  　　　　　　　　　　　　　　　　　　　 D.a<c<b

12.在Rt△ABC中，∠C=90°，下列式子中不一定成立的是

A.tanA=　　　　　　　　　　　　　　　　　 　　　 B.sin²A+sin²B=1

C.sin²A+cos²A=1　　　　　　　　　　　　　　　　　　　 D.sinA=sinB

13.在△ABC中，若sinA－+(1－tanB)²=0，则∠C的度数是

A.45°　　　　  　　　　　　　B.60°　 　　　　 C.75°　　　　   D.105°

14.已知△ABC中，∠C=90°，∠A=60°，BC+AC=3+，则BC等于

A. 　　　　　　　　　　　　B.3　　　　  　　　　C.2　　　　　　　　 D. +1

15.若等腰三角形腰长为4，面积是4，则这个等腰三角形顶角的度数为

A.30°　　　　  　　　　　　　B.30°或150°　　 C.60°　　　　   D.60°或120°

16.某人沿着坡度为1∶的山坡前进了1000 m，则这个人所在的位置升高了

A.1000 m　　　　  　B.500 m　　　　  　C.500 m　　  D. m

三、考查你的基本功(共24分)

17.(16分)计算或化简：

(1)sin45°·cos60°－cos45°·sin30°;

(2)5tan30°－2(cos60°－sin60°).

(3)(tan30°)²⁰⁰⁵·(2sin45°)²⁰⁰⁴;

(4)(2cos45°－tan45°)－(tan60°+sin30°)⁰－(2sin45°－1)^－1.

18.(8分)已知△ABC中，∠C=90°，AC=m，∠BAC=α(如图4),求△ABC的面积.(用α的三角函数及m表示)

　　　　　　　　　　　　　　　

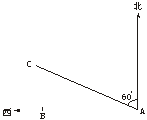
图4　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　图5

四、生活中的数学(共18分)

19.(9分)“郑集中学”有一块三角形形状的花圃ABC，现可直接测量到∠A=30°，AC= 40 m，BC=25 m，请求出这块花圃的面积.

20.(9分)如图5，某货船以20海里/小时的速度将一批重要的物资由A处运往正西方向的B处，经16小时的航行到达，到达后便接到气象部门通知，一台风中心正由A向北偏西60°方向移动，距台风中心200海里的圆形区域(包括边界)均会受到影响.在B处的货船是否会受到台风的侵袭？说明理由.

五、探究拓展与应用(共10分)

21.(10分)(1)如图6中①、②，锐角的正弦值和余弦值都是随着锐角的确定而确定，变化而变化，试探索随着锐角度数的增大，它的正弦值及余弦值的变化规律.

　　　　　　　　　　　　　　

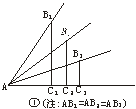
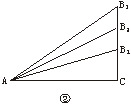
图6

(2)根据你探索到的规律，试分别比较18°、34°、50°、62°、88°这些锐角的正弦值的大小和余弦值的大小.

参考答案

一、1.　　2.60°　　3.30　4.　5.60°6.30°　7.60°　　8.26

二、9.A　10.B　11.A　12.D　13.C　14.B　15.B　16.B

三、17.(1)0;(2);(3);(4)－2.

18.解：∵tanα=，

∴BC=AC·tanα=m·tanα.

S_△ABC=AC·BC=m²tanα.

四、19.解：作CD⊥AB.

∵∠A=30°,

∴CD=AC=×40=20(m),

AD==20(m),

BD==15(m).

(1)当∠ACB为钝角时，AB=AD+BD=20+15,

∴S_△ABC=AB·CD=(20+15)×20=(200+150)(m²).

(2)当∠ACB为锐角时，AB=AD－BD=20－15.

∴S_△ABC=AB·CD=(20－15)×20=(200－150)(m²).

20.解：AB=16×20=320(海里),

作BD⊥AC垂足为D.

∵∠BAC=30°,∴sin30°=，BD=AB·sin30°=160.

∵160<200,∴B处的货船会受到影响.

五、21.(1)由图①知

sinB₁AC₁=，sinB₂AC₂=，

sinB₃AC₃=.

∵AB₁=AB₂=AB₃且B₁C₁>B₂C₂>B₃C₃,

∴>>.

∴sinB₁AC₁>sinB₂AC₂>sinB₃AC₃.

而∠B₁AC₁>∠B₂AC₂>∠B₃AC₃,

而对于cosB₁AC₁=,

cosB₂AC₂=,

cosB₃AC₃=.

∵AC₁<AC₂<AC₃,

∴cosB₁AC₁<cosB₂AC₂<cosB₃AC₃.

而∠B₁AC₁>∠B₂AC₂>∠B₃AC₃.

由图②知sinB₃AC=,

∴sin²B₃AC=.

∴1－sin²B₃AC=1－

==.

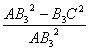同理,sinB₂AC=，1－sin²B₂AC=，

sinB₁AC=，1－sin²B₁AC=.

∵AB₃>AB₂>AB₁,∴<<.

∴1－sin²B₃AC<1－sin²B₂AC<1－sin²B₁AC.

∴sin²B₃AC>sin²B₂AC>sin²B₁AC.

∵∠B₃AC，∠B₂AC，∠B₁AC均为锐角,

∴sinB₃AC>sinB₂AC>sinB₁AC.

而∠B₃AC>∠B₂AC>∠B₁AC.

而对于cosB₃AC=,

cosB₂AC=,

cosB₁AC=.

∵AB₃>AB₂>AB₁,∴<<.

∴cosB₃AC<cosB₂AC<cosB₁AC.

而∠B₃AC>∠B₂AC>∠B₁AC.

结论：锐角的正弦值随角度的增大而增大，锐角的余弦值随角度的增大而减小.

(2)由(1)知

sin18°<sin34°<sin50°<sin62°<sin88°,

cos18°>cos34°>cos50°>cos62°>cos88°.