相似三角形试卷
(时间120分钟 满分:150)
安徽省望江县沈冲中学:齐永丰
一、选择题:(30分)
1.已知![]() ,则下列各式中不正确的是
( )
,则下列各式中不正确的是
( )
A、ad=bc
B、![]() C、
C、![]() D、
D、![]()
2.已知 x:y=3:2,则下列各式中不正确的是( )
A、= B、= C、= D、=
3、若x是3和6的比例中项,则x的值为 ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4.若![]() ,则k的值为
( )
,则k的值为
( )
A、2 B、-1 C、2或-1 D、不存在
5.在△ABC中,∠A∶∠B∶∠C=1∶2∶3,CD⊥AB于D,AB=![]() ,则DB=( )
,则DB=( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
6.如果点C为线段 AB的黄金分割点,且AC>BC,则下列各式不正确的是( )
A.AB:AC=AC:BC B.AC=![]() AB
AB
C、AC=![]() AB D.AC≈0.61 8AB
AB D.AC≈0.61 8AB
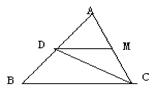
7.如图,在△ABC中,CD平分∠ACB,过D作BC的平行线交AC于M,若BC=m,AC=n,则DM=( )
 A、
A、![]() B、
B、![]()
C、![]() D、
D、![]()
8.已知D、E为△ABC的边AB、AC上的两点,且AB=8,AC=6,AD=4,AE=3,则![]() ∶
∶![]() =( )
=( )
A、1∶2 B、1∶4 C、1∶3 D、2∶5
9. 如下图,在△ABC中,若∠AED=∠B,DE=6,AB=10,AE=8,则BC的长为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()


10.ABC是锐角三角形,正方形DEFG的一边在BC上,其余两个定点分别在AB、AC上,记△ABC的面积为![]() ,正方形DEFG的面积为
,正方形DEFG的面积为![]() ,则有 ( )
,则有 ( )
A、![]() B、
B、![]() C、
C、![]() D
D![]()
二、填充题:(40分)
11.若x是3、5、7的第四比例项,则x__________
12、在比例尺为1∶40000的平面图上,5.2平方厘米所表示的实际面积为_______平方米。
13.已知:x∶y∶z=2∶3∶4,则![]() 的值为 。
的值为 。
 14.在打网球时,击球点距球网的水平距离为8m , 已知网高为0.8m ,要使球恰好能打过网,而且落在离网4m的位置,则球拍击球的高度h为________m
14.在打网球时,击球点距球网的水平距离为8m , 已知网高为0.8m ,要使球恰好能打过网,而且落在离网4m的位置,则球拍击球的高度h为________m
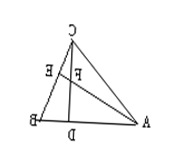
15.如图,在△ABC中,D、E为AB、BC上两点,若![]() ,
,
则![]() 的值为
。
的值为
。
16.已知,△ABC中,D、E分别是AB、AC边的中点,BC=6,则DE=_________,△ADE与△ABC的周长比是___________
17.一个直角三角形的两条直角边的比是1∶2,那么斜边上高把斜边分成两部分的比是
18.在Rt△ABC中,AD为斜边上的高,![]() ,则AB∶BC= 。
,则AB∶BC= 。
19.△ABC的中位线EF交中线AD于G,则△AGE与△ABC的面积之比为__________.
20.在等边三角形ABC中,点D,E分别在AB,AC上,且DE∥BC,如果BC = 8 cm ,AD : AB = 1 : 4 ,那么△ADE的周长等于___________cm
三、解答题:
21、作图:(15分)
(1)已知线段AB,求作一点P,使点P分AB成定比3∶4。
A ________________ B
(2)已知线段a、b、c,求作一线段x,使x=![]() 。
。
a b c
22、(20)四边形ABCD是平行四边形,点F在BA的延长线上,连接CF交AD于点E,1)、求证:△CDE∽△FAE,2)当E是AD的中点,且BC = 2CD时,求证:∠F = ∠BCF
23. (20)已知,如图,Rt△ABC中,∠ACB=900,AB=5,两直角边AC、BC的长是关于x的方程![]() 的两个实数根。
的两个实数根。
(1)求m的值及AC、BC的长(BC>AC)
(2)在线段BC的延长线上是否存在点D,使得以D、A、C为顶点的三角形与△ABC相似?若存在,求出CD的长;若不存在,请说明理由。


24、(25)如图,已知过A(2,4)分别作x轴、y轴的垂线,垂足分别为M、N,若点P从O点出发,沿OM作匀速运动,1分钟可到达M点,点Q从M点出发,沿MA作匀速运动,1分钟可到达A点。
(1)经过多少时间,线段PQ的长度为2?
(2)写出线段PQ长度的平方y与时间t之间的函数关系式和t的取值范围;
(3)在P、Q运动过程中,是否可能出现PQ⊥MN?若有可能,求出此时间t;若不可能,请说明理由;
(4)是否存在时间t,使P、Q、M构成的三角形与△MON相似?若存在,求出此时间t;若不可能,请说明理由;
![]() y
y
N A
Q
![]()


![]()
![]()
O P M