新题型训练（寒假）　　 姓名：_________

1. 现有标号为a₁，a₂，…，a₂₀₀₄的盒子，按标号从小到大的顺序排放，已知a₁中有7个球，a₂中有8个球，且任意相邻的四个盒子装球总数为30个，那么a₂₀₀₄盒子中有__________个球。

2. 在圆环形路上有均匀分布的四家工厂甲、乙、丙、丁，每家工厂都有足够的仓库供产品储存. 现要将所有产品集中到一家工厂的仓库储存，已知甲、乙、丙、丁四家工厂的产量之比为1∶2∶3∶5. 若运费与路程、运的数量成正比例，为使选定的工厂仓库储存所有产品时总的运费最省，应选的工厂是（　　 ）

A、甲　　　 B、乙　　　 C、丙　　　　D、丁

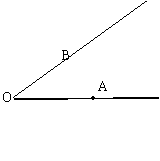
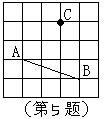
3. 如图，已知图中每个小方格的边长为1，则点C到AB所在直线的距离等于_______

				·

4. 如图，已知方格纸中的每个小方格都是全等的正方形，∠AOB画在方格纸上，请在小方格的顶点上标出一个点P，使点P落在∠AOB的平分线上。

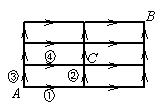
5. 如图，游人从董永公园中的景点A到景点C有两条路径可走，即A经到C，或由A经到C，那么按照图中箭头所标明的方向（只能向上，向右行走），由景点A到景点B的不同路径有（　）．

A．6条　　　B．8条　　　C．10条　　　D．12条

6. 某市的一家报刊摊点从报社买进一种晚报，其价格为每份0.30元，卖出的价格为0.50元，卖不掉的报纸可以退还给报社，不过每份退还的钱数与退还的报纸的数量关系如下：

退还的数量	5	10	15	20	25	30或30以上
价格（元/份）	0.25	0.20	0.15	0.10	0.05	0.02

现经市场调查发现，在一个月中（按30天记数）有20天可卖出150份/天，有10天只能卖出100份/天，而报社规定每天批发给摊点的报纸的数量必须相同.

（1）通过在坐标系中（以退还的钱数为纵坐标，退还的报纸数量为横坐标）描出点，分析出退还的钱数y（元）与退还的报纸数量k（份）之间的函数关系式.

（2）若该家报刊摊点每天从报社买进的报纸数x份（满足100<x<150），则当买进多少报纸时，毛利润最大？最多可赚多少钱？

7. 某市部分初三学生参加了2005年全国初中数学竞赛决赛，并取得优异成绩. 已知竞赛成绩分数都是整数，试题满分为140分. 现随机抽样统计300名参赛学生的成绩分数分布情况如下：

分数段	0－19	20－39	40－59	60－79	80－99	100－119	120－139
人数	0	37	68	95	58	30	12

请根据以上信息解答下列问题：

（1）经竞赛组委会评定，竞赛成绩在100分以上（含100分）的考生均可获得不同等级的奖励，试估计该市参加本次数学竞赛决赛考生的获奖比例；

（2）你认为该市本次决赛成绩分数的中位数最有可能落在哪个分数段内？

（3）上表还提供了其他信息，例如：“样本中获奖的人数为42人”等等，请你再写出两条此表提供的信息；

（4）若某同学平时数学学习成绩一直都处于班级前3名（所在班级人数50人），在本次数学竞赛中，他未得奖. 这属于哪一类事件？（可能事件、不可能事件、必然事件）

8.某班为了从甲、乙两同学中选出班长，进行了一次演讲答辩与民主测评，A、B、C、D、E五位老师作为评委，对“演讲答辩”情况进行评价，全班50位同学参与了民主测评，结果如下表所示：

	A	B	C	D	E
甲	90	92	94	95	88
乙	89	86	87	94	91

	“好”票数	“较好”票数	“一般”票数
甲	40	7	3
乙	42	4	4

表1演讲答辩得分表（单位：分）　　　　  表2民主测评票数统计表（单位：张）

规定：演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定：民主测评得分=“好”票数×2+“较好”票数×1分+“一般”票数×0；综合得分=演讲答辩得分×（1-a）+民主测评得分×a（0.5≤a≤0.8）。

（1）a=0.6时，甲的综合得分是多少？

（2）a在什么范围时，甲的综合得分高？a在什么范围时，乙的综合得分高？

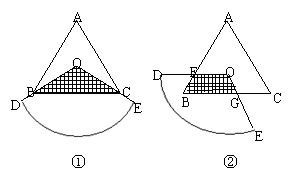
9. 如图①，扇形ODE的圆心O重合于边长为3的正三角形ABC的内心O，扇形的圆心角

∠DOE=120º，且OD＞OB。将扇形ODE绕点O顺时针方向旋转（旋转角a满足条件：

Oº＜a＜120º，四边形OFBG是旋转过程中扇形与三角形的重叠部分（如图②）。

（1）在上述旋转过程中，CG，BF有怎样的数量关系？四边形OFBG的面积有怎样的变化？证有你发现的结论；

（2）在上述过旋转过程中，设CG=x，连接FG，设△OFG的面积为y，求y与x之间的函数关系式，并写出自变量x的取值范围；

（3）设扇形ODE的半径是5/2，在（2）的前提下，是否存在某一位置，使△OFG的面积小于扇形ODE面积的1/20？若存在，求出此时x的值；若不存在，说明理由。

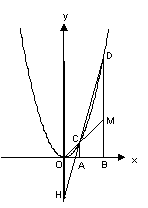
10.数学课上，老师出示图和下面框中条件，

如图6，在直角坐标平面内，O为坐标原点，A点坐标为（1，0），

点B在x轴上且在点A的右侧，AB=OA.过点A和B作x轴的垂线，

分别交二次函数y=x的图象于点C和D.直线OC交BD于点M,直线

CD交y轴于点H.记点C、D的横坐标分别为x、x，点H的纵坐标为y。

同学发现两个结论：①S：S_梯形ABMC=2：3；　②数值相等关系：x·x=－y。

（1）　 请你验证结论①和结论②成立；

（2）　 请你研究：如果将上述框中的条件“A点坐标为（1，0）”改为“A点坐标为（t，0），（t>0）”，其它条件不变，结论（1）是否仍成立？（请说明理由）　　　　　　　　　

（3）　 进一步研究：如果将上述框中的条件“A点坐标为（1，0）”改为“A点坐标为（t，0）（t>0）”，又将条件“y=x”改为“y=ax（a>0）”，其它条件不变，那么x、x和y有怎样的数值关系？（写出结果并说明理由）　　　　　　　　　　　　

（1）通过作图，知y＝mk+n，　

当0<k<30,且为整数, y＝﹣0.1k+0.3；当k≥30 , y=0.02.

　 （2） S=2×0.2x＋100×10×0.2－(0.3－y)(x－100)=　4x＋200－0.1(x－100)

=﹣0.1x＋24x－800.

当x=﹣＝120时，即每天买进120份报纸时，可获最大毛利润为640元

（1）14%；

（2）60－79；

（3）如“样本中在60分以下（不含60分）的有105人”，“样本中没获奖的占大多数，达到86%”等；

（4）可能事件．

26．解：（1）若抛物线y＝x²－(a＋2)x＋9的顶点在y轴上，由顶点的横坐标为0，得a=2；若抛物线y＝x²－(a＋2)x＋9的顶点在x轴上，由△=0得a=4或a=－8．

（2）根据题意得a=4，此时抛物线为y＝x²－6x＋9．解得所以A（0，9）、B（7，16）．

①由于点P在上y=x+9上，因此设符合题意的点P的坐标为（t，t+9），此时对应的点Q的坐标为（t，t²－6t＋9），由题意得PQ=(t+9) －(t²－6t＋9)=6，解得t=1或6，由题意0<t<7，点P的坐标为（1，10）或（6，15）；

②设在线段AB上是否存在这样的点P，使得△ABQ∽△OAC，∴∠BAQ=∠AOC=90°，分别过B、Q两点向y轴作垂线，垂足为E、H，由∠BAQ=90°，注意到直线y=x+9与x轴所夹的锐角为45°，由QH=AH可求得点Q的坐标为（5，4），但显然AB∶AQ≠OA∶OC，∴△ABQ与△OAC不可能相似，∴若线段AB上不存在符合条件的点P．

解：（1）由已知可得点B的坐标为（2，0），点C坐标为（1，1），点D的坐标为（2，4），由点C坐标为（1，1）易得直线OC的函数解析式为y=x，

∴点M的坐标为（2，2），∴S=1,S_梯形ABMC=,∴S:S_梯形ABMC=2:3,即结论①成立；

设直线CD的函数解析式为y=kx+b，则　　 得

∴直线CD的函数解析式为y=3x－2；由上述可得，点H的坐标为（0，－2），y=－2，

∵x·x=2，∴x·x=－y，即结论②成立；

（2）结论①仍成立

∵点A的坐标为（t，0）（t>0），则点B坐标为（2t，0），从而点C坐标为（t，t），点D坐标为（2t，4t），设直线OC的函数解析式为y=kx，则t=kt，得k=t，

∴直线OC的函数解析式为y=tx，设点M得坐标为（2t，y），∵点M在直线OC上，

∴当x=2t时，y=2t，点M的坐标为（2t，2t），∴S:S_梯形ABMC=·2t·t：（t+2t）=2：3，∴结论①仍成立；

（1）　 x·x=－y由题意，当二次函数的解析式为y=ax（a>0）,且点A坐标为

（t，0）（t>0）时，点C坐标为（t，at），点D坐标为（2t，4at），

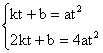设直线CD的函数解析式为则， 得

∴直线CD的函数解析式为y=3atx－2at，

则点H的坐标为（0，－2at）， ，∵x·x=2t，∴x·x=－y