第二十二章 一元二次方程单元检测题

　　　　　 班级：________　　姓名：________　学号：______　得分:___________

一、选择题（2分×10=20分）

1．（x-3）²=x-3的解为（　）

　　A．x=2　　B．x=4　　C．x=3　　D．x=3或x=4

2．用配方法解下列方程时，配方有错误的是（　）

　　A．x²-2x-99=0化为（x-1）²=100　　B．2t²-7t-4=0化为（t-）²=

　　C．x²+8x+9=0化为（x+4）²=25　　  D．3x²-4x-2=0化为（x-）²=

3．已知y=x²-5x-6，要使y的值为0，x的取值为（  ）

　　A．2或-3　　 B．-2或3　　C．6或-1　　D．-6或1

4．要使方程（a-3）x²+（b+1）x+c=0是关于x的一元二次方程，则（　）

　　A．a≠0　　　　　　　 B．a≠3

　　C．a≠1且b≠-1　　　 D．a≠3且b≠-1且c≠0

5．下面是某同学在九年级期中测试中解答的几道填空题：（1）若x²=a²，则x= a ；

（2）方程2x（x-1）=x-1的根是 x=0 ；（3）若直角三角形的两边长为3和4，则第三边的长为 5 ．其中答案完全正确的题目个数为（　）

　　A．0　　 B．1　　 C．2　　 D．3

6．下面四个方程中，两根之和为2的是（　）

　　A．x²-2x+4=0　　 B．x²+2x-4=0　　C．x²-2x-4=0　　D．x²+2x+4=0

7．若关于x的一元二次方程3x²+6x+k=0有实数根，则（　）

　　A．k>3　　 B．k<3　　 C．k≥3　　　D．k≤3

8．下面对于二次三项式-x²+4x-5的值的判断正确的是（　）

　　A．恒大于0　　B．恒小于0　　C．不小于0　　D．可能为0

9．某超市一月份的营业额为200万元，一月、二月、三月的营业额共1000万元，如果平均每月增长率为x，则由题意列方程为（　）

　　A．200（1+x）²=1000　　　　B．200+200×2×x=1000

　　C．200+200×3×x=1000　　　D．200[1+（1+x）+（1+x）²]=1000

10．将进货单价为70元的某种商品按零售价100元/个售出时每天能卖出20个，若这种商品的零售价在一定范围内每降价1元，其日销售量就增加1个，为了获得最大利润，则应降价（　）

　　A．5元　　B．10元　　C．15元　　D．20元

二、填空题（3分×10=30分）

11．方程（3x+1）²-6x=2的二次项系数为______，一次项系数为______，常数项为_________．

12．若方程（m-1）x^m+1-2x=4是一元二次方程，则m=________．

13．x²-10x+_____=（x-_______）²

14．已知关于x的方程x²+3x+k²=0的一个根是-1，则k=_______．

15．以下四个方程①x²-4x+1=0，②y²-y+3=0，③x²+9=6x，④x（5x+21）=20，其中有实数根的方程是_________．（填写你认为正确的答案的序号）．

16．已知代数式x²+x的值为6，则x=_______，代数式2x²+2x+3的值为_______．

17．当x=______时，与既是最简根式又是同类根式．

18．已知（x²+2x-3）⁰=x²-3x+3则x=________．

19.在参加足球世界杯预选赛的球队中，每两个队都要进行两次比赛，

共要比赛72场，则参加的球队数为_______．

20.在一块长35米，宽26米的矩形绿地上有宽度相同的三条小路， (第19题)

如图，其中绿地面积为850m²，若设小路宽为X,则可列出方程为　　　　　　　　　　 .

三、解答题（50分）

21．用适当方法解下列方程（每小题3分，共12分）

（1）　　　　　　　　　　 （2）x-=5x（-x）

（3）　　　　　　　　　　 （4）(x+1)²-4(x+1)+4=0

22．（6分）已知实数a、b、c满足+│b+1│+（c+3）²=0，求方程ax²+bx+c=0的根．

23.(6分)将进货单价为40元的某种商品按50元的价格售出时,能卖500个,已知该商品每涨价1元时,其销量就减少10个,为了赚8000元的利润,售价应定为多少?这时应进货多少个?

a

D

A

24.(8分)有长为30米的篱笆，一面利用墙（墙长a=16米），围成中间隔有一道篱笆的长方形花圃，设花圃的宽AB为x米，面积为S平方米。

C

B

25、(8分)设某人驾车正以108km/h的速度沿平直高速公路行驶，根据有关人员推算和测试，该汽车行驶时的安全距离（从刹车到车完全停止行驶的距离）为90m，

（1）从开始刹车减速到完全停止约用了多长时间？

（2）那么该车减速后平均每秒减少多少米？

（3）从开始刹车后滑行到45m处时约用了多长时间？

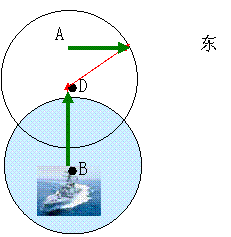
26.(10分)某军舰以20节的速度由西向东航行,一艘电子侦察船以30节的速度由南向北航行,它能侦察出周围50海里(包括50海里)范围内的目标.如图,当该军舰行至A处时,电子侦察船正位于A处的正南方向的B处,瓶AB=90海里.如果军舰和侦察船仍按原来速度沿原方向继续航行,那么航行途中侦察船能否侦察到这艘军舰 ?如果能,最早何时能侦察到?如果不能,请说明理由.

	北

　　　　　　　　　　　　　　　　　　　  　　

27（5记入总分,加到满分为止）阅读材料，解答问题:

材料：为解方程（x²-1）²-5（x²-1）+4=0我们可以将x²-1视为一个整体，然后设x²-1=y，则（x²-1）²=y²，原方程可化为y²-5y+4=0，解得y₁=1，y₂=4，当y=1时，x²-1=1，∴x²=2，∴x=±；当y=4时，x²-1=4，∴x²=5，∴x=±，∴原方程的解为x₁=，x₂=-，x₃=，x₄=-，

解答问题：

（1）填空，在解原方程得到①的过程中利用_________法达到了降次的目的，体现了_______数学思想;

（2）利用上述方法解方程x⁴-x²-6=0