2004年中国数学奥林匹克暨第十九届冬令营试题

（第一天）

（2004年1月8日上午8：00～12：30　 澳门）

　　　　　　　　

1. 凸四边形EFGH的顶点E,F,G,H分别在凸四边形ABCD的边AB,BC,CD,DA上，满足，而点A,B,C,D分别在凸四边形E₁F₁G₁H₁的边E₁F₁, F₁G₁, G₁H₁, H₁E₁上，满足E₁F₁∥EF，F₁G₁∥FG，G₁H₁∥GH，H₁E₁∥HE．已知，求的值．

2. 已知正整数c，设数列满足：

，且，

其中[x]表示不大于x的最大整数．

求数列的通项公式．

3. 设M是平面上n个点组成的集合，满足：

（1）M中存在7个点，是一个凸七边形的7个顶点；

（2）M中任意5个点，若这5个点是一个凸五边形的5个顶点，则此凸五边形内部至少含有M中的一个点．

求n的最小值．

2004年中国数学奥林匹克暨第十九届冬令营试题

（第二天）

（2004年1月9日上午8：00～12：30　 澳门）

4. 给定实数a和正整数n，求证：

（1）存在唯一的实数数列满足：

；

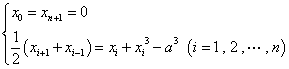（2）（1）中的数列满足．

5. 给定正整数n≥2，设正整数满足：

以及≤1．

求证：对任意实数x，有≤．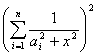

6. 证明：除了有限个正整数外，其他的正整数n均可表示为2004个正整数之和，且满足：