上海市初中数学竞赛（浦东新区选拔赛）

暨浦东新区初中数学竞赛试卷

（本试卷共有15题，第1~5题，每题6分，第6~10题，每题8分，第11~15题，每题10分，满分120分）

1．如果关于x的方程的解是非负数，那么k的取值范围是　　　　　  ．

2．已知那么=　　　　　  ．

3．如果直线被两条坐标轴截得的线段长为5，那么这条直线在y轴上的截距是　　　　　  ．

4．已知矩形纸片ABCD中，AB=4，BC=8，将这张纸片沿对角线BD折叠，那么折叠后纸片重叠部分的面积是　　　　　  ．

5．如果，那么=　　　　　  ．

6．如果 ，，，那么=　　　　　  ．

7．如图，四边形ABCD和四边形CEFG都是正方形，

AB=5，那么△BDF的面积等于　　　　　  ．

8．已知，那么=　　　　　  ．

9．抛物线与x轴的两个交点分别位于点（2，0）的两旁，那么a的取值范围是　　　　　  ．

10．在Rt△ABC中，两条直角边AC、BC的长分别为8厘米和15厘米，点D在边AB上，点E在边AC上，CD与BE相交于点F，且，那么CD=　

1．已知实数a、b、c满足，，那么=　　　　　  ．

12．已知，在梯形ABCD中，AD∥BC，AD<BC，AB=CD，AC=BC=10，如果这个梯形高的长度与边AD的长度相等，那么这条高的长度等于　　　　　　．

13．如图，已知OC是∠AOB的平分线，点P在OC上，且

OP=2厘米，∠AOB=60°，过点P的动直线交OA于点D，

交OB于点E，那么=　　　　　  厘米．

14．某校初三100名学生排成一行，从1起依次报数，凡报奇数者出队；留下的学生重新从1起依次报数，报奇数者出队；这样反复下去，那么最后留下的一位学生第一次报的数应是　　　　　  ．

15．某高速公路收费站，有m（m>0）辆汽车排队等候收费通过．假设通过收费站的车流量（每分钟通过的汽车数量）保持不变，每个收费窗口的收费检票的速度也是不变的．若开放一个收费窗口，则需20分钟才可能将原来排队等候的汽车以及后来接上来的汽车全部收费通过；若同时开放两个收费窗口，则只需8分钟也可将原来排队等候的汽车以及后来接上来的汽车全部收费通过．若要求在3分钟内将排队等候收费的汽车全部通过，并使后来到站的汽车也随到随时收费通过，那么至少要同时开放　　　　 个收费窗口．

参考答案：

1．原方程化为3x=4-k

由x≥0得4-k≥0,

∴k≤4

2.两式相加得a²+2ab+b²=25

　(a+b)²=25,a+b=±5

3. ∵直线y=2x+b交y轴于A(0,b), 交x轴于B(,0),AB=5

　 ∴b²+=5²,解得b=.

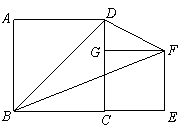
4. 如图:

 

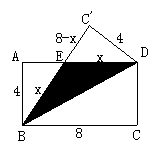
　易得EB=ED,设为x.

由x²=4²+(8-x)², 得x=5,8-x=3

∴ΔDEC^/的面积=6

　而ΔBDC^/的面积=16

∴ΔBED的面积=16-6=10

5.　　　 原式化为

  ∴

  ∴x=1,y=3,x+y=4.

6.　　　 原式取倒数得

　

　三式相加得.

7.

 如图应有：，x=

∴DM=5-x=

∴ΔBDF的面积=

　=

8. ∵x≠0,将x²-3x+1=0的两边除以x得

∴

∴

∴ .

9.由题意有x=2时y<0

　∴4-2(2a+1)+2a-5<0

　∴.

10.

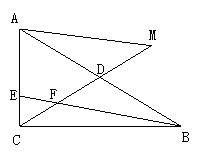
　如图,倍长FN到M,连结AM.

　由已知得

  ∴AM//EF，

　∵DF=DM

　∴AD=DB

　∴CD=

11．由题知是方程x²-6x+c²+9=0的两根,

  ∴

  ∴c=0

　∴a=b=3

　∴原式=0

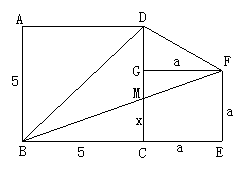
12.

　

　如图：,

  ∵DE²+EF²=FD²

　∴,

 ∴DE=a=6.

13.当时有OD=OE=4

　∴.

14.答案：64.

15.设每分增加a辆车，要求在3分钟内将排队等候收费的汽车全部通过，并使后来到站的汽车也随到随时收费通过，那么至少要同时开放x个收费窗口．

　则有

  ∴.