适应性考试试卷(非实验区)　　　　　 姓名

一．填空题：（每小题3分）

1．的相反数是　　　　　 ；

2．如图1，AB∥ED，BC∥EF，如果∠B，那么∠E =　　　；

3．分解因式：；

4．已知点P是半径为的⊙O内一定点，且，则过点P的最短的弦长

是  　　　　　　；

5．已知点P（，）在双曲线上，则；

6．若5个正整数的中位数是3，众数是7且唯一，则这5个正整数的和是　　 ；

7．已知二次函数的部分图象（如图1所示）

由图象可知关于的一元二次方程的两个根

分别是，；

8．某学校一次数学考试中，初三（1）班50人平均分81.5分，初三（2）班45人平均分83.4分，这两个班95名学生的平均分是　　　　　　  ；

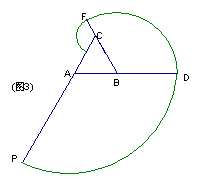
9．如图3，有一边长为的等边三角形ABC木块，

点P是以CA的延长线上的点，在A、P之间拉

一条细绳，绳长AP为，拉直细绳AP，把

它紧紧在⊿ABC木块上缠绕，（缠绕时木块不动）

点P运动的路线长为：　　　　　　  ；

10．等腰梯形高为，且对角线互相垂直则这个梯形的

面积是

二．大题。（每小题4分）

11．有一种病毒非常微小，其半径为0.，用科学计数法表示这种病毒的半径约为　　　　　　　　　　　　　　　　　　　　　  　　　　　 （　 ）

（A）（B）（C）（D）

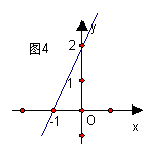12．能表示如图4所示的一次函数图象的解析式是　　　　　　　　　　  （　 ）

（A） 　（B）

（C）  （D）

13．有五条线段，长度分别为1、2、3、5、7，从中任取三条，他们一定能构成三角形的个数是　　　　　　　　　　　　　　　　　　　　　　　　　 （　 ）

（A）　 10个　　（B）　　7个　 （C）　　4个　　（D）　　1个

14．为筹备班级的成长毕业联欢会，班长对全班学生喜欢那种水果进行民意调查，以决定最终买什么水果，下面的调查数据中最值得关注的是　　　　　   （　 ）

（A）　 中位数　 （B）　　平均数　 （C）　　 众数　　（D）　　方差

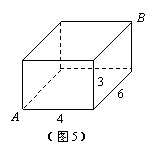15．如图是一块长、宽、高分别是6，4和3的长方体木块.一只蚂蚁要从长方体木块的一个顶点处，沿着长方体的表面到长方体上和相对的顶点处吃食物，那么它需要爬行的最短路径的长是　　　　　　　　　　　 （　　）

（A）　　 （B）

（C） 　　（D）  

三．解答题：

16．（8分）

先化简，再选择使原式有意义而你喜欢的数代入求值：

17．（10分）某班数学兴趣小组，对市公交9路车起点一个星期乘车人数进行统计，以每天1000人次为准，超过的人数记为正数，不足人数记为负数，记录如下：

　　 ，，，100，，177，230

（1）求该起点站这一星期里，平均每天乘客人数（2分）

（2）照这样估计2005年4月份该起点站乘客约有多少人次？（3分）

（3）若将2005年4月份起点站每天乘客人数进行整理后，分成五组画出频率分布直方图中（不要求画频率分布直方图），每组的饿频率之比依次为：，能否判断这个月该车站乘客人数的中位数一定落在哪个小组？说明理由；

18．认真阅读下列对话：（10分）

小明：（递上10元钱）阿姨，我买一盒饼干和一袋牛奶；

售货员（阿姨）：小朋友，你的运气真好，如果昨天你用10元钱买一盒饼干后，用剩余的钱再买一袋牛奶就不够了，不过，今天是儿童节，给你的饼干打9折，两样东西拿好，另退你8角钱。

小强：一盒饼干的标价是整数哦！

根据对话的内容，试求出饼干和牛奶的标价：

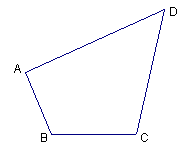
19．顺次连结四边形ABCD（如图6）各边的中点的四边形是平行四边形吗？如果是，请给出证明。（要求在原图上画出图形，写出已知、求证、证明）；如果不是，请说明理由；

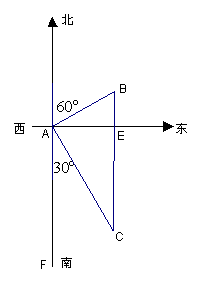
20．（10分）甲船在A处测得B处的乙船的方位角是北偏东，此时乙船正向正南驶去，若甲船从南偏东方向以每小时9海里的速度前进，3小时追上乙船，求最初甲、乙两船的距离和乙船的速度；（结果精确到0.1）

21．（10分）

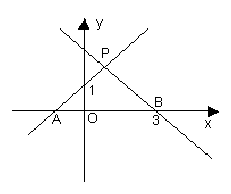
如图7，直线PA是一次函数

的图象，直线PB是一次函数

的图象；

（1）试求、的值；

（2）求⊿PAB的面积；

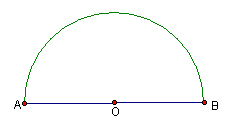
22．如图8，有一块半圆形的木块，现要把它截成三角形板块，三角形的两个顶点为A、B，另一顶点在弧AB上，问怎样截取才能使截出的面积最大。（要求说明理由）

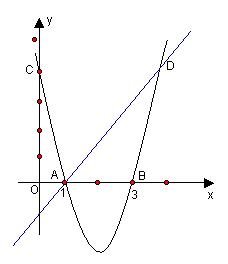
23．已知二次函数的图象如图9所示，它与轴相交于点C，点D在二次函数图象上与点C对称，一次函数的图象过点A、D；（10分）

（1）求点D的坐标；（4分）

（2）求一次函数的解析式；（6分）

24．某企业投资100万元引进一条农产品生产线，若不计维修、保养费用，设计投产后每年可创利33万元，该生产线投产后，从第一年到地年的维修、保养费用累计为（万元），且，若第1年维修、保养费为2万元，第2年的为6万元，

（1）求的解析式；（6分）

（2）投产后，这个企业在第几年就能收回投资？（6分）

25.（10分）如图10，是一个正方形纸片，根据要求多次分割成若干个小直角三角形，操作过程如下：

第一次分割，将正方形纸片分成4个全等直角三角形；

第二次分割：将上次得到的4个直角三角形中的一个再分割成4个全等直角三角形；

以后按第二次分割的作法继续进行下去；

（1）请你在图10中画出第一次和第二次分割的图案；

（2）设正方形纸片的边长为，请你通过操作和观察，将第二次、第三次分割所得的最小的直角三角形面积（S）分别填入下表（6分）

分割次数（）	1	2	3	------
最小直角三角形的饿面积（S）

（3）请写出第次分割所得的最小直角三角形的面积；

适应性考试试卷(非实验区)参考答案：

一：填空题：（每小题3分）

1．； 2．； 3．； 4．； 5．； 6．； 7．； 8．；

9．；　10．；

二．选择题。（每小题4分）

11．B； 12．A； 13．D； 14．C； 15．A；

三．解答题：

16．解：原式——————（3分）

（4分）

（5分）

（6分）

当时，代入计算正确得分2分；

17．解：（1）（人）

（2）（人）

（3）因为把30个数依次大小排列，中位数是第15、16个数的平均数，又第一、第二组频数之和为15，第16个数落在第三组，因此无法确定中位数落在哪个小组。

18．解：设饼干的标价为元，牛奶的标价为每袋（）元，（2分）依题意有：

------------（6分）

解得：

∵为整数，∵

∴元

答：略

19．是平行四边形（1分）

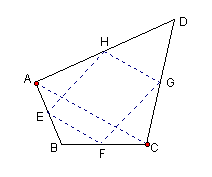已知：四边形ABCD各边中点依次是E、F、G、H；（2分）

求证：四边形EFGH是平行四边形；（3）分

证明：连结AC（4分）在⊿ABC中

∵E、F分别是AB、BC的中点，

∴EF∥AC，EF =AC（6分）

同理在⊿ADC中

∵H、G分别是AD、CD的中点

HG∥AC，HG =AC（8分）

∴HG∥EF，且HG = EF（9分）

∴四边形EFGH是平行四边形（10分）

20．解：如图，有∠BAE =，∠CAE =，

∴⊿ABC为直角三角形　　　　 （2分）

AC =（海里）　　　　 （4分）

∠C =∠FAC =　　　　　　  （5分）

由，可得（7分）

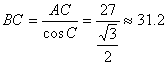由，可得（或）

设乙船的速度为海里/时，则（海里）（9分）

答：最初甲、乙两船的距离是海里和乙船的速度是海里/时。

21．解：作OC⊥AB交弧AB于点C，连结AC、BC，

则截得的∠ABC的面积最大。

证明：

在弧AB上任取一点D，（不同于点C）

连结AD、BD，过点D作DE⊥AB于E，则

，

连结OD，在Rt⊿ODE中，，，

∴

∴

23．解：

（1）∵D在二次函数的图象上且与点C对称，则D（4，3）（4分）

（2）设直线过点A（1，0）和D（4，3）

∴　　（8分）

解得：（9分）

∴所求一次函数为（10分）

24．解：

（1）　　由题意，当时，；时，；（2分）

∴　 （4分）

∴

∴所求二次函数解析式为：

（2）略

25．解：

（1）　　分割方案如图所示为：（2分）

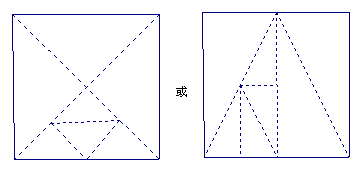分割的方案还有很多，学生给出正确的都给满分；

（2），（8分）；（3），没有给出的范围不扣分；