初三数学阶段性练习问卷 2006、3
考生须知：
1、本练习卷分问卷和答卷两部分，满分120分，考试时间100分钟。
2、必须在答卷的对应答题位置答题。
3、答题前，应先在答卷上填写班级、姓名、学号。
一、选择题（本题有15个小题，每小题3分，共45分）
下面每小题给出的四个选项中，只有一个是正确的，请把正确选项前的字母填在答题卷中相应的格子内
1、已知实数：
，
，0，
，
，1.，cos30º，0.……，其中无理数的个数有
A、2个 B、3个 C、4个 D、5个
2、下列说法中正确的是
A、近似数1.70与近似数1.7的精确度相同
B、近似数五百与近似数500的精确度相同
C、近似数4.70×104是精确到百分位的数，它有三个有效数字
D、近似数24.30是精确到百位的数，它有三个有效数字
3、如果4x-3是多项式4x2+5x+a的一个因式，则a等于
A、-6 B、6 C、-9 D、9
4、已知三角形的两边a =3，b =7，第三边是c，且a＜b＜c，则c的取值范围是
A、4＜c＜7 B、 7＜c＜10 C、4＜c＜10 D、 7＜c＜13
5、已知y =x+a，当x = -1，0，1，2，3时对应的y的平均数为5，则a的值是
A、
B、
C、
D、4
6、某种型号的空调器经过3次降价，价格比原来下降了30%，则其平均每次下降的百分比（精确到1%）应该是
A、11.2% B、33.1% C、26.0% D、8.5%
7、已知一个直角三角形的两边长恰好是方程2x2-8x+7=0的两根，则这个直角三角形的斜边长是
A、
B、3 C、6 D、9
8、在平面直角坐标系中，若一点的横坐标与纵坐标互为相反数，则该点一定不在
A、直线y = -x上 B、抛物线y =x2上
初三数学问卷—1（共4页）
C、直线y = x上
D、双曲线y =
上
9、已知二次函数y =ax2+bx+c，且a＜0，a-b+c＞0，则一定有
A、b2-4ac＞0 B、b2-4ac=0 C、b2-4ac＜0 D、b2-4ac≤0
10、轮船往返于一条河的两码头之间，如果船本身在静水中的速度是固定的，那么，当这条河的水流速度增大时，船往返一次所用的时间将
A、增多 B、减少 C、不变 D、增多、减少都有可能
11、一个圆形餐桌直径为2米，高1米，铺在上面的一个正方形桌布的四个角恰好刚刚接触地面，则这块桌布的每边长度（米）为
A、2
B、4 C、4 D、
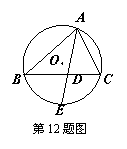
12、如图，已知△ABC内接于⊙O，AE平分∠BAC，交BC于D，交
⊙O于E，若AB、AC的长是方程x2-ax+12=0的两实根，AD=2，则
AE的长为
A、5 B、6 C、7 D、8
13、
的值最接近于
A、1 B、
C、
D、
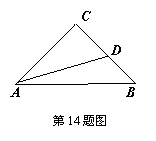
14、如图，在等腰直角三角形ABC中，∠C=90º，AC=6，D是BC上
一点，若tan∠DAB=
,则AD的长为
A、2
B、
C、
D、8
15、这是一个古老的传说，讲一个犯人利用概率来增加他得到宽恕的机会。给他两个碗，一个里面装着5个黑球，另一个里面装着除颜色不同外其它都一样的5个白球。把他的眼睛蒙着，然后要选择一个碗，并从里面拿出一个球，如果他拿的是黑球就要继续关在监狱里面，如果他拿的是白球，就将获得自由。在蒙住眼睛之前允许他把球混合，重新分装在两个碗内（两个碗球数可以不同）。你能设想一下这个犯人怎么做，使得自己获得自由的机会最大？则犯人获得自由的最大机会是 A、 B、
C、 
D、
二、填空题（每题4分，共20分）
16、在正数范围内定义一种运算“△”，其规则是a△b
=
，根据这一规则，方程
初三数学问卷—2（共4页）
x△(x+1)=
的解是
。
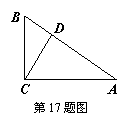
17、如图，AC⊥BC，CD⊥AB，且AB=5，BC=3，则
的值
为 。
18、如图，已知二次函数，y1=ax2+bx+c(a≠0)与一次函数y2=kx+m
(k≠0)的图像相交于点A（-2，4），B（8，2）。则能使y1＜y2
成立的x的取值范围是 。
19、已知实数x满足（x2-x）2-4(x2-x)-12=0，则代数式
x2-x+1的值为 。
20、在日常生活中，你会注意到有一些含有特殊数字规律的车牌
号码，如：浙A80808 ，浙A22222 ，浙A12321 等，这些牌照
中的五个数字都是关于中间的一个数字“对称”的，给人以对称美的感受，我们不妨把这样的牌照叫做“数字对称”牌照。如果让你负责制作只以8或9开头且有5个数字的“数字对称”牌照，那么最多可制作 个。
三、解答题（共55分）
解答应写出文字说明、证明过程或推演步骤。
21、（本题满分7分）
⑴ 计算 
⑵已知a ，b为实数，试比较
与
的大小。
22、（本题满分8分）
解方程（组）
⑴ 
⑵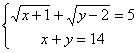
23、（本题满分8分）
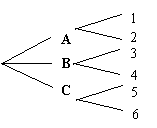
请你依据右面图框中的寻宝游戏规则，探究“寻宝
游戏”的奥秘：
⑴用树状图表示出所有可能的寻宝情况；
⑵求在寻宝游戏中胜出的概率。
初三数学问卷—4（共4页）
24、（本题满分10分）
已知a，b互为相反数，
⑴计算：a+b ，a2-b2，a3+b3 ，a4-b4，……的值。
⑵用数学式子写出⑴中的规律，并证明。
25、（本题满分10分）
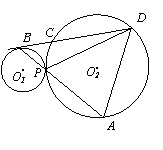
如图，⊙O1与⊙O2外切于点P，过⊙O1上的一点B作⊙O1的切线，交⊙O2于C、D，直线BP的延长线交⊙O2于A，连结DP、DA。
⑴求证：△ABD∽△ADP。
⑵若AD=2，BP=3，求AB的长。
26、（本题满分12分）
如图，将一块直角三角形纸板的直角顶点放在C（1，）处，两直角边分别与x,y轴平行，纸板的另两个顶点A，B恰好是直线y=kx+
与双曲线y=
(m＞0)的交点。
⑴ 求m和k的值。
⑵ 设双曲线y=(m＞0)在A，B之间的部分为L，让一把三角尺的直角顶点P在L上滑动，两直角边始终与坐标轴平行，且与线段AB交于M，N两点，请探究是否存在点P，使得MN=AB？写出你的探究过程和结论。
初三数学问卷—4（共4页）
初三数学阶段性练习参考答案
2006、3
一、选择题
1—5：C、C、A、B、D 6—10：A、B、D、A、A 11—15：A、B、B、C、D
二、填空题
16、x=1 17、
18、-2<x<8 19、7 20、200
21、（1） -2+
（2）作差：
；① 当a=b时，=；② 当a>b时，>③ 当a<b时，<
22、（1）解得： x1=， x2=
（2）
，
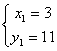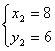
23、 （1）
（2）
24、（1）∵a=-b； ∴ a+b=0 ， a2-b2=0, a3+b3=0, a4-b4=0…… an+(-1)n+1 bn=0
（2）证明：分类，当n为奇数时：an+bn=0；当n为偶数时：an-bn=0
25、（1）过点P作两圆的公切线KH，则∠ADP=∠APH=∠KPB=∠B,
∠A=∠A，∴△ABD∽△ADP（2）由△ABD∽△ADP，及
，
得到：AD2=AB×AP，设AP=x，则：（2）2=（x+3）x；解得： x1=4,
x2=-7（舍去）∴ AB=7
26、（1）K=-,m=4 （2）假设存在点P使得MN=AB，
∵AC∥y轴，MP∥y轴，∴AC∥MP，∴∠PMN=∠CAB ∴Rt△ACB∽Rt△MPN
∴ 
，设点P（x,
），（1<x<8），则M(x,-
),
∴MP=
,又AC=
∴ 
即，2x2-11x+16=0
∵ △=（-11）2-4×2×16=-7<0 ∴方程无实数根。
所以不存在点P使得MN=AB