九年级毕业班质量检测

数学试题

(满分：150分：考试时间：120分钟)

说明：①可以携带使用科学计算器，并注意运用计算器进行估算和探究；

②未注明精确度、保留有效数字等的计算问题不得采取近似计算．

一、填空题(本大题共10小题，每小题3分，共30分)

1．计算：　－3＝________。

2．如图是某物体的三视图，那么该物体形状是________。

3．计算：＝________

4．因式分解：x²－6x十9＝________

5．已知圆柱的母线长为4cm，侧面积为24πcm²，则这个圆柱的底面半径是________cm．

6．某电视台综艺节目接到热线电话5000个，现要从中抽取“幸运观众”10名，小明打通了一次热线电话，他成为“幸运观众”的概率是________。

7．如图，AB是⊙O的直径，C、D是⊙O上的点，∠D＝35⁰，

则∠BOC的度数是________

8．李先生要用按揭贷款的方式购买一套商品房，由于银行提

高了贷款利率，他想尽量减少贷款额，就将自己的全部积蓄a

元交付了所需购房款的60％，其余部分向银行贷款，则李先生

应向银行贷款________元．

9．某班27名男同学的平均身高是1.70米，23名女同学的平均身高是1.6O米，则该班同学的平均身高是________米．(结果精克到0.0l米)

10．如图，直线y=kx十1与x轴交点的横坐标为2，若将该直线向左平移1个单位，则所得直线与两坐标轴所围成的三角形面积为________(平方单位)

二、选择题(本大题共6小题，每小题4分，共24分．每小题都有四

个备选答案，请把你认为正确的一个答案的代号写在题后的括号内)

11．下列运算正确的是　　(　　)

　  A，　2^－2＝－4　　B．　(a^-3)⁴十(a³)⁴＝a⁰

　  C．a²·a³=a⁶　　D．(—a)(－a)²=-a³

12．下列抽样调查选取样本的方法较为合适的是　　(　　)

A．为估计南平2005年的平均气温，晓丹查询了南平2005年2月份的平均气温

B．为了解全班同学期末考试的平均成绩，老师抽查了成绩前5名同学的平均成绩

C．妈妈为了检查烤箱里的饼是否熟了，随手取出一块尝试

D．为了解九年级学生的平均体重，小红选取了即将参加校运会的运动员做调查

13．如图，过双曲线y＝(k是常数，k＞0，x＞0)的图象上两点A、8分别作AC⊥x轴于C，BD⊥x轴于D，则△AOC的面积S₁和△BOD的面积S₂的大小关系为(　　)

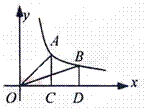　  A．S₁>S₂

　  B．S₁＝S₂

　  C．S₁<S₂

　  D．S₁和S₂的大小无法确定

14．如图，正五边形ABCDE中，DC和AB的延长线交于F，则图中

与△DBF相似的三角形有(不再添加其他的线段和字母，不包

括△DBF本身)　　(　　)

　  A．1个　　B．2个

　  c．3个　　D．4个

15．随意转动图中两转盘上的指针，指针静止在如图所示的情形时

(即蓝色和绿色相配)的概率为　　(　　)

A、　　　　　 B、　　　　　 C、　　　　　 D、

16、⊙O上有两点A、B，∠AOB是小于平角的角，将∠AOB绕着圆心O旋转，当点B旋转到A时，点A旋转到C，如果点C和旋转前的点B关于圆心O成中心对称，则∠AOB＝( 　)

A、45⁰　　　　　B、60⁰　　　　　C、90⁰　　　　　D、135⁰

三、解答题(本大题共10小题，共96分)

17、(7分)先化简，再求值：

(a＋b)(a－b)＋b(b－2)，其中a＝，b＝－1。

18、(7分)解不等式组：，并把解集在数轴上表示出来。

19、(8分)如图，在□ABCD中，将△ABD沿对角线BD对折，得到△A’BD。请在图中用直尺和圆规按题意完成作图(不写作法，保留作图痕迹)，并证明：∠A’＝∠C。

20、(8分)解分式方程：

21、(8分)下图中的方格图均是由边长为1的小正方形组成的，现通过图形变换将图1中阴影部分的图形割补成一个正方形。其思想方法是：由于要拼成的正方形的面积为“5”(由5个小正方形组成)，则正方形的边长为，而＝。因此，具体做法是：①连结A₁A₃、A₁A₅；②将△A₁A₂A₃绕A₃沿顺时针方向旋转90⁰；③将△A₁A₅A₆绕A₅沿逆时针方向旋转90⁰；④将小正方形A₁A₆A₇A₈先向左平移2个单位，再向上平移1个单位。图中四边形A₁A₃A₄A₅即是所求作的正方形。仿照此方法将图2中的阴影部分的图形割补成正方形。(要求：直接在图上画出图形，并写出一种具体做法。)

22、(8分)某市九年级学生参加了该市期末数学教学质量检查考试，试卷满分为100分。现　随机抽样统计300名学生的数学成绩，分数分布情况如下：

分数段	0-29	30-39	40-49	50-59	60-69	70-79	80-89	90-100
人　数

　  请根据以上信息解答下列各题：

(1)若小红平时数学成绩经常处于班级前5名，在本次数学考试中，她得了75分．这属于______事件：(填：“必然”、“可能”或“不可能”)

（2)上表提供了许多信息，例如：“样本中及格(≥60分)人数为244人”等，请你再写出两

条此表提供的信息；

(3)若规定成绩在80分以上(含80分)的为优秀，请估计该市九年级学生此次数学考试成绩的优秀率(精确到l%)；

(4)上表中数学考试成绩分数的中位数落在哪个分数段内?能否确定分数的众数?　(直接回答，不必说明理由!)

23．(lO分)如图，AB是⊙O的直径，C为AB延长线上的—点，CD交⊙O 于点D，  且∠A=∠C=30°。

(1)说明CD是⊙O的切线：

(2)请你写出线段BC和AC之间的数量关系，并说明理由。

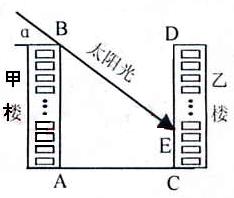24．(12分)下图为某小区的两幢1O层住宅楼，由地面向上依次为第1层、第2层、…、第10层，每层的高度为3m，两楼间的距离AC=30m．现需了解在某一时段内，甲楼对乙楼的采光的影响情况．假设某一时刻甲楼楼顶B落在乙楼的影子长EC=h，太阳光线与水平线的夹角为α．

(1)用含α的式子表示h；

(2)当α＝30°时，甲楼楼顶B的影子落在乙楼的

第几层?从此时算起，若α每小时增加10°，几小

时后，甲楼的影子刚好不影响乙楼采光．

　　

25．(14分)在某次数字变换游戏中，我们把整数O，1，2．…，100称为“旧数”，游戏的变换规则是：将旧数先平方，再除以100，所得到的数称为“新数”．

(1)请把旧数80利26按照上述规则变换为新数：

(2)经过上述规则变换后，我们发现许多旧数变小了．有人断言：“按照上述变换规则，所有的新数都不等于它的旧数．”你认为这种说法对吗?若不对，请求出所有不符合这一说法的旧数：

(3)请求出按照上述规则变换后减小了最多的旧数(要写出解答过程)．

 26．(14分)如图，已知：Rt△ABC中，∠C=90°，AC=BC=2，将一块三角尺的直角顶点与斜边AB的中点M重合，当三角尺绕着点M旋转时，两直角边始终保持分别与边BC、AC交于D，E两点(D、E不与B、A重合)．

　(1)求证：MD=ME；

　(2)求四边形MDCE的面积：

　(3)若只将原题目中的“AC=BC=2”改为“BC=a，AC=b，(a≠b)”其它都不变，请你探究：MD和ME还相等吗?如果相等，请证明；如果不相等，请求出MD∶ME的值．

参考答案

一、填空题

1、3　　2、圆锥　　 3、3　　4、(x－3)²　5、3　　6、1/500或0.02　　 7、110⁰

8、　9、1.65　　 10、

二、选择题

11、D　 12、C　 13、B　 14、B　 15、A　　　 16、C

三、解答题

17、解：原式＝a²－b²＋b²－2b＝a²－2b

　　当a＝，b＝－1时，原式＝()²－2×(－1)＝4

18、解不等式①，得：x＜2

解不等式②，得：x≥－1

∴原不等式组的解集是：－1≤x＜2

19、解：由作图知，△A’BD是由△ABD沿BD对折所得，故△A’BD≌△ABD，

∴　∠A’＝∠A，

又∵四边形ABCD是平行四边形，

∴∠A＝∠C

∴∠A’＝∠C

20、解：两边同时乘以x＋2，得：

　　　　7＝1－3x－2（x＋2）

　　　　10＝－5x

　　　　x＝－2

　　当x＝－2时，x＋2＝0

　　∴x＝－2是原方程的增根，舍去

　　∴原方程无解

21、略

22、⑴、可能

⑵、①样本中，本次考试不及格人数是56人；②样本众数落在80－89分数段中；

⑶、样本优秀率是：≈48%

由此估计，该市九年级学生此次数学考试成绩的优秀率约为48%。

⑷、中位数落在70－79分数段；不能确定分数的众数。

23、解：⑴连结地BD、OD

∵AB是直径，∴∠ADB＝90⁰

∵∠A＝30⁰，

∴∠ABD＝60⁰，∴△OBD是等边三角形

而∠ABD＝∠B＋∠BDC

∴∠BDC＝∠ABD－∠B＝30⁰

∴∠ODC＝90⁰

即OD⊥DC，故DC是⊙O的切线

⑵、BC＝AC

∵OD⊥DC，且∠C＝30⁰，∴BD＝BC

又在Rt△ABD中，∠A＝30⁰，

∴BD＝AB，

∴BC＝AB，

∴BC＝AC

24、⑴过E作EF⊥AB，垂足为F，则∠BEF＝α

　　　在Rt△AFE中，FE＝AC＝30，AB＝10×3＝30

　　　∴BF＝AB－EC＝30－h

　　　∵tanα＝，∴BF＝EF×tanα

　　　即30－h＝30×tanα

　　　h＝30－30tanα

⑵、当α＝30⁰时，h＝30－30tan30⁰≈12.68

　　∴甲楼顶B的影子落在第五层

⑶、不影响乙楼的采光时，AB的影子顶部应刚好落在C处，

　　此时，AB＝30，AC＝30，

∴∠BCA＝45⁰，

则∠α’＝45⁰，

∵角α每小时增加10度，

∴应在1个半小时后，甲楼的影子刚好不影响乙楼的采光。

25、解：⑴、＝64，＝6.76

⑵、不对。　　设这个数为x，则＝x

　　∴x²＝100x

　  ∴x₁＝0，x₂＝100

　　∴符合这一说法的旧数有0和100。

⑶、设减少的量为y，则y＝x－＝－(x²－100x)＝－(x－50)²＋25

　  ∴当x＝50时，y有最大值，是25

　　即变换后减少最多的旧数是50。

26、⑴、证明：在Rt△ABC中，M是AB的中点，且AC＝BC，

　　∴CM＝ AB＝BM

　　∠CMA＝∠B＝45⁰，CM⊥AB

　　而∠BMD＝90⁰－∠DMC，∠EMC＝90⁰－∠DMC，

　　∴∠BMD＝∠EMC

　　△BDM≌△CEM（ASA）

　　∴MD＝ME

⑵、∵△BDM≌△CEM，∴S_{四边形DMEC}＝S_△DMC＋S_△CME＝S_△DMC＋S_△BMD＝S_△BCM＝S_△ACB＝1，

　　∴四边形MDCE的面积为1

⑶、不相等。

如图所示，过M点作MF⊥BC于F，MH⊥AC于H，

∵M是AB的中点，

∴MF＝b，MH＝a

∠FMD＝90⁰－∠DMH，∠EMH＝90⁰－∠DMH，故∠FMD＝∠EMH

∠MFD＝∠MHE＝90⁰，

∴△MFD≌△MHE，

∴