2006年初中学业考试数学试题
班级________姓名_______
一、 选择题：（40分）
1、某计算机运算速度为每秒次，保留四个有效数字，用科学记数法表示每秒的次数为-----------------------------------------------------------------------（ ）
A、3.8×1011 B、3.840 ×1011 C、3.84×1012 D、3.840×1012
2、用1、2、3三个数字排成一个三位数，排出是偶数的概率是-------------（ ）
A、
B、
C 、
D、
3、三角形两边长分别为3和6，第三边是方程x2-6x+8=0的根，则这个三角形的周长是----------------------------------------------------------------------------------------------（ ）
A、11 B、13 C、11或13 D、11和13
4、如图，数轴上表示1，
的对应点分别为A、B，点B关于点A的对称点为C，则点C所表示的数是--------------------（ ）
Ａ-1 Ｂ、1- Ｃ、2- Ｄ、-2 0 C A B x
| 最高气温 | 23 | 24 | 25 | 26 |
| 天数 | 3 | 2 | 1 | 4 |
５、某地连续１０天的最高气温统计如下表：
则这组数据的中位数和平均数分别为---（ ）
Ａ、２４.５ ，２４.６ Ｂ、２５，２６ Ｃ、２６，２５ Ｄ，２４，２６
6、抛物线y=2x2-3x+1的顶点坐标为----------------------------------------------（ ）
A、（-
，
） B、（，-） C、（，）D、（-，-）
7、
如图，在⊙O中，弦AB=1.8cm，∠ACB=30º则⊙O的直径是 ---（ ）
A、0.9 cm B、1.8 cm C、3.6 cm D、2.0 cm
8、在正方形铁皮上剪一个圆形和扇形，使之恰好围成
一个圆锥模型，设圆的半径为r，扇形的半径为R，
则R与r的关系式为----------------------（ ）
A、R=
r B、R=4r C、R=3r D、R=2r
9、一人沿坡比为1：
的斜边AB滑下，滑下的距离S米与时间t秒的关系式S=10t+2t2,如果滑到坡底的时间为4秒，则此人水平移动的距离为---------（ ）
A、36 米 B、18
米
C、72 米 D、36米
10、A班做（1）题，B班做（2）题。
（1）相交两圆半径是
和
，公共弦为4，则圆心距是 ---------------（ ）
A、 +1
B、
-1 C、 ±1 D、7
（2）
二次函数y=x2+bx+1的图象如图所示，如果a,b是方程x2+bx+1=0的两根，则a+b的值一定是---------（ ）
A、小于1 B 、大于4
C、等于1 D、大于2且小于4
二、 填空题（30分）
11、函数y=
中自变量x的取值范围是_______________________.
12、分解因式：2x3-8x=___________________________.
13、用计算器计算·sin40º=
______________________ （保留三个有效数字）
14、⊙O的半径为5，圆心O到直线l的距离为3，则直线l与⊙O的位置关系是____________.
15、抛物线y=ax2+bx+c开口向上，对称轴直线x=1，A（-2，y1），B（0，y2）, C（2，y3）在该抛物线上，则y1, y2, y3,的大小关系是_______________________________.
16、（1）、（2）两题，任选一题：
（1） 关于x的元一元二次方程kx2-6x+9=0有两个不相等的实根，则k的取值范围是______________________________.
（2） 点A（1，0），点B在直线y=-x上运动，当线段AB最短时，点B的坐标是_______________________________.
三、解答题（80分）
17、（1）计算: -22+(
)º+2sin30º (4分)
（2）化简求值:
÷(
-x-2) 其中x=-1 (4分)
18、（1）解方程:
=
(4分)
2(x+2)≤3x+3
（2）解不等式组 
< 
并写出不等式组的整数解.(4分)
19、小明和小王做硬币游戏，连续抛四次硬币，当其中恰好有三次结果相同时小明赢，而当恰好有两次结果相同时，小王赢，其他情况不计算输赢，你认为该游戏对双方公平吗？ (8分)
20、矩形ABCD中，AD=9cm,AB=3cm ，
（1） 将其折叠，使点D与点B重合，求DE和EF 的长，
（2） 将其折叠，使AB落到BC上，求此时折痕的长度。(8分)
A D
B
C
21、如图,一块长x m为,宽为y m的矩形草地由篱笆围着,并且由一条与长边平行的篱笆分开,篱笆总长为600 m.
(1) 
用含x的代数式表示矩形草地的面积S
(2) 
求矩形草地的最大面积.
22、（12分 ）等腰梯形ABCD的边BC在x轴上，点A在y轴的正半轴上，A（0，6），D(4,6)且AB=2
.（1）求点B的坐标.
（2）求经过A、B、D三点的抛物线的解式。
(3)在（2）中所求的抛物线上是否存在一点P，使得S△PBC=
S梯形ABCD？如果存在，请求出P点坐标，如果不存在，请说明理由。
23、（12分）如图，AB为⊙O的直径，AC为弦，CD⊥AB于点D，如果AE=AC，BE交⊙O于点F，连接CF，DE。求证：（1）AE2=AD·AB
(2)∠ACF=∠AED
C
B A
D
E
24、（14分）已知二次函数y=
x2-
x+6的图象与x轴交于A、B两点，与y轴交于C点.（1）求A、B、C三点坐标
（2）求过B、C两点的一次函数的解析式，
（3）如果P（x,y）是线段BC上的动点，试求△POA 的面积S与x之间的关系式。
（4）是否存在点P，使△APO为等腰三角形，如果存在，求出点P的坐标。
附加题：（任选一题，满分5分，如果试卷总分超过150分，仍记为150分）
（1） 一个梯形的4 条边的长分别为1、2、3、4，求次梯形的面积。
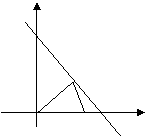
(2)有一块三角形纸片，要求剪拼成一个正直三棱柱，使它的表面积与原正三角形面积相等。（画出剪割线，并用必要的文字说明）