2006年高中阶段学校招生考试
数学科
一、选择题(每小题给出4个答案，其中只有一个正确的，请把所选的答案的字母写在题目后面的括号内）
1．用科学记数法表示3 390 000，正确的是（ ）.
A．339×104 B．33.9×105 C．3.39×106 D．0.339×107
2．下列计算中，正确的是（ ）.
A.
B．
C．
D．
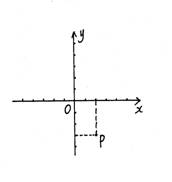
3．
如图所示，点
的坐标是（ ）
A．
B．
C．
D．
|
中，
，
，
，则
A．
B．
C．
D．
5．若两圆的半径分别是3㎝和5㎝，两圆的圆心距是2㎝，则两圆的的位置关系是（ ）.
A．内切 B．外切 C．相交 D．内含
6．函数
与函数
的图象在同一平面直角坐标系内的交点个数是（ ）
A．一个 B．二个 C．三个 D．零个
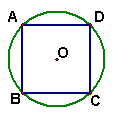7．如图，若四边形ABCD是半径为1的⊙O的内接正方形，
则图中四个弓形（即四个阴影部分）的面积和为（ ）.
A．（2π－2）㎝2 B．（2π－1）㎝2
|
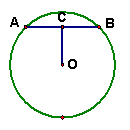8．如图，在半径为5的⊙O中，如果弦AB的长为8，
那么它的弦心距OC等于（ ）.
A．2 B．3 C．4 D．6
9．用配方法解一元二次方程
则方程可变形为（
）.
|
B．
C．
D．
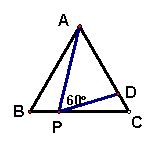
10．如图，在等边△ABC中，P为BC上一点，D为AC上一点，
且∠APD=60°，BP=1，
，则△ABC的边长为（ ）.
|
二、填空题
11．
已知点M与点N（－1，3）关于原点对称，则M的坐标是
.
12．计算：
= .
|
的一个根是另一个根的2倍，则m的值是
.
14．如图，已知AB∥DE，∠ABC=80°，∠CDE=140°，则∠BCD= .
15．已知抛物线
经过点（1，2）与（-1，4），则
的值是
三、解答题
16．先化简，再求值：
，其中
17．解不等式组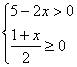
，在数轴上表示解集，并说出它的自然数解.
18．在一块矩形铁皮上有一点P，现要在这块铁皮上剪去一个等腰直角三角形，把它加工成零件，请你在已知矩形ABCD上求作这个等腰直角三角形，使它的直角顶点为P，斜边落在AD上.（要求尺规作图，保留作图痕迹，不必写作法和证明）
|
19．要用21张白卡纸做包装盒，每张白卡纸可以做盒身2个，或者做盒底盖3个.一个盒身和两个底盖做成一个包装盒.现把这些白卡纸分成两部分，用多少张做盒身，多少张做底盖，正好配套？
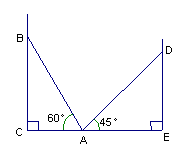20．如图，在两面墙之间有一个底端在A点的梯子，当它靠在一侧墙上时，梯子的顶端在B点；当它靠在另一侧墙上时，梯子的顶端在D点.已知∠BAC=60°，∠DAE=45°，点D到地面的垂直距离DE=3
m.求点B到地面的垂直距离BC.
| |
21、 青少年视力水平下降已引起全社会的广泛关注.为了解某市初中毕业年级6000名学生的视力情况，我们从中抽取一部分学生的视力作为样本进行数据处理，得到如下的频率分布表和频率分布直方图：
| 分组 | 频数 | 频率 |
| 3.95~4.25 | 2 | 0.04 |
| 4.25~4.55 | 8 | 0.16 |
| 4.55~4.85 | 0.40 | |
| 4.85~5.15 | 16 | 0.32 |
| 5.15~5.45 | 4 | |
| 合计 | 1 |
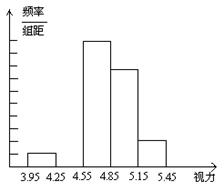
(1)根据上述数据，补全频率分布表和频率分布直方图；
(2)若视力在4.85以上属于正常，不需矫正，试估计该市6000名初中毕业生中约有多少名学生的视力需要矫正．
22、如图在 ABCD中，AB = 4cm，BC = 1cm，E是CD边上一动点，AE、BC的延长线相交于点F。设DE = x（cm），BF = y（cm）
(1)求y（cm）与x（cm）之间的函数关系式，并写出自变量x的取值范围；
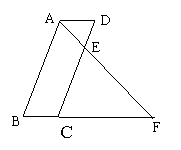(2)画出此函数的图象；
| |
23．阅读材料：多边形上或内部的一点与多边形各顶点的连线，将多边形分割成若干个小三角形．
（1）图（一）给出了四边形的具体分割方法，分别将四边形分割成了２个、３个、４个小三角形．
（2）请你按照上述方法将图（二）中的六边形进行分割，并写出得到的小三角形的个数．试把这一结论推广至n边形.
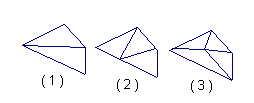
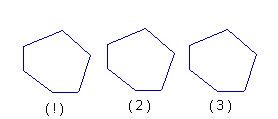
图（一） 图（二）
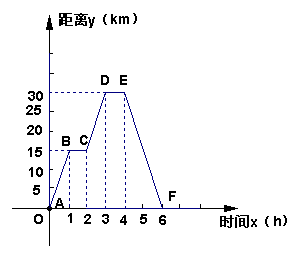24．小明同学骑自行车去郊外春游，如图表示他离家的 距离y（km）与所用的时间x（h）之间关系的函数图象.
（1）根据图象回答：小明到达离家最远的地方需几小 时？此 时离家多远？
（2）求小明出发两个半小时离家多远？
（3）求小明出发多长时间距家12km？
| |