探索型问题练习
 1、已知在梯形A BCD中，AD∥BC，AD＜BC，AD＝5，AB＝DC＝2.

(1) P为AD上的一点，满足∠BPC＝∠A.①求证：△ABP∽△DPC；②求AP的长.

(2)如果点P在AD边上移动(点P与点A、D不重合)，且满足∠BPE＝∠A，PE交直线BC于点E，同时交直线DC于点Q，那么①当点Q在线段DC的延长线上时，设AP＝x，CQ＝y，求y关于x的函数解析式，并写出函数的定义域；②当CE＝1时，写出AP的长(不必写出解题过程).

2、已知抛物线y＝2 x- 4 x＋m与x轴交于不同的两点A、B，其顶点是C，点D是抛物线的对称轴与x轴的交点.

(1)求实数m的取值范围；　

(2)求顶点C的坐标和线段AB的长度(用含有m的式子表示)；

(3)若直线y＝x＋1分别交x轴、y轴于点E、F:问△BDC与△EOF是否有可能全等，如可能，请证明，如不可能，请说明理由.

3、在半径为6，圆心角为90°的扇形OAB的上，有一动点P,　PH⊥OA,　垂足为H ,△OPH的重心为G .

(1)当点P在AB上运动时，线段GO、GP、GH中，有无长度保持不变的线段？如有，请指出该线段，并求出其长度；

(2)设PH＝x， GP＝y，求y关于x的函数解析式；

(3)如果△PGH是等腰三角形，试求出线段PH的长.

4、如图，直线y＝x＋2分别交x:y轴于点A、C，P是该直线上在第一象限内的一点，PB⊥x轴，B为垂足，S△ABP＝9:(1)求点P的坐标；(2)设点R与点P在同一个反比例函数的图象上，且点R在直线PB的右侧，作RT⊥x轴，T为垂足，当△BRT与△AOC相似时，求点R的坐标.

5、已知a,b,c分别是ΔABC的∠A，∠B，∠C的对边(a>b)，二次函数y=(x-2a)x-2b(x-a)+c²的图象，顶点在x轴上，且sinA,sinB是关于x的方程(m+5)x²-(2m-5)x+m-8=0的两个根。
（1）判断ΔABC的形状，并说明理由.
（2）求m的值.
（3）若这个三角形的外接圆面积为25π，求ΔABC的内接正方形（四个顶点都在三角形三边上）的边长.

6、某房地产公司要在一块地（图中矩形ABCD）上规划建造一个小区公园（矩形GHCK），为了使文物保护区ΔAEF不被破坏，矩形公园的顶点G不能在文物保护区内，已知AB=200m, 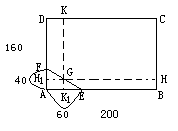AD=160m, AE=60m, AF=40m.
（1）求矩形小区公园的顶点G恰是EF的中点时，公园的面积.
（2）当G在EF上什么位置时，公园面积最大？

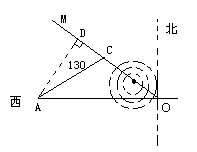7、某校的教室A位于工地O的正西方向，且OA=200米，一部拖拉机从O点出发，以每秒5米的速度沿北偏西53°方向行驶，设拖拉机的噪声污染半径为130米，试问教室A是否在拖拉机的噪声污染范围内？若不在，请说明理由；若在，求出教室A受污染的时间有几秒？（已知：sin53°≈0.80, sin37°≈0.60, tan37°≈0.75）（福州）

8、如图的曲线表示一辆自行车离家的距离与时间的关系，骑车者九点离开家，十五点回家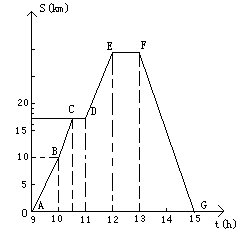，根据这个曲线图，请你回答下列问题.
（1）到达离家最远的地方是什么时间？
（2）何时开始第一次休息？休息多长时间？
（3）第一次休息时，离家多远？
（4）11：00到12：00，他骑了多少千米？
（5）他在9：00～10：00和10：00～10：30的平均速度各是多少？
（6）他在何时至何时停止前进并休息用午餐？
（7）他在停止前进后返回，骑了多少千米？
（8）返回时的平均速度是多少？
（9）11：30和13：30时，分别离家多远.
（10）何时距离家22千米？

9、有一批货，如果月初售出，可获利1000元，并可得本利和再去投资，到月末获利1.5%；如果月末售出这批货，可获利1200元，但要付50元保管费，请问这批货在月初还是月末售出好？

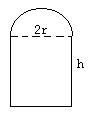10、某水库的闸板如图所示，它的形状是由一个半圆和一个矩形组合而成，为了周围封得好，周长应尽可能小，但为了使水的流量越大越好，希望面积尽可能地大，问当周长一定时半圆半径r和矩形高度h应怎样取才好呢？

11、已知抛物线y=x²+kx+1与x轴相交于两个不同的点A、B，顶点为C，且∠ACB=90°，试求如何平移此抛物线使其∠ACB=60°.

12、已知平面直角坐标系内两点A(-2 , 0 ), B(4 , 0), 点P在直线y=x+上，且ΔABP为直角三角形，求：

（1）点P的坐标；（2）经P，A，B三点且对称轴平行于y轴的抛物线是否存在？若存在，求出抛物线的解析式.

13、已知过定⊙O的直径AB的两端及　　上任一点E作⊙O的三条切线AD，BC和CD。它们分别交于D，C点，求证AD·BC是定值.

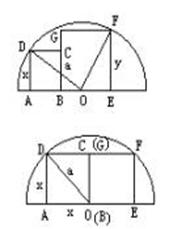
14、如图，半径为a的半圆内有两正方形ABCD，BEFG，点D、F在半圆周上，点C，G在半圆内.
(1)试证明截得的这两个正方形的面积和为定值;
(2)判别DO与OF的位置关系.
　　

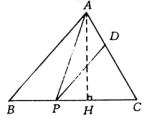15、如图，△ABC中，BC=4，AC=2，∠ACB=60°，P为BC上一点，过点P作PD//AB，交AC于D.　连结AP，问点P在BC上何处时，△APD的面积最大？

 

探索型问题练习参考答案

1、（1）AP的长为1或4.　　　　  （2） y＝-x2＋x-2 (1＜x＜4).

2、（1）m＜2

（2）顶点C的坐标为(1，m-2) ，线段AB的长度为;

（3）△BDC与△EOF有可能全等.

3、（1）GH长度保持不变为2.

　（2）y＝(0＜x＜6)

（3） 若GH＝GP，无解;　

若PH＝GP，即x＝y，x＝;　

若PH＝GH，而GH＝2，所以PH＝2.

4、(1) P点坐标为(2，3).　　(2)　　 y＝.

5、（1）ΔABC是RtΔ.  　（2）m=20. 　（3）或.

6、（1）公园的面积为GH×KG=170×140=23800(m²).
　（2）S=(200-x)(160-40+x) = -(x-10)²+
　　∴ 当x=10时，S_max=,
　　即G在EF上，且到AD的距离为10m时公园面积最大.

7、过A作AD⊥OM，AD=200·sin37°≈200×=120(米)
∵ AD=120<130米，
∴ 教室A在拖拉机的噪声污染范围内，设当拖拉机到达点C时，教室A受污染，即AC=130.
　　在RtΔADC中，DC==50（米） 从C到D所用时间t=50÷5=10秒，
　　在经过这样一段时间A才能脱离污染，共20秒.　　

8、（1）12点，30千米
　（2）10点半，半小时
　（3）离家17千米
　（4）11：00到12：00，他骑了13千米
　（5）9：00～10：00的平均速度为10千米/时，

10：00～10：30的平均速度是14千米/时
　（6）12点到13点
　（7）返回骑了30千米
　（8）2小时，15km/h.
　（9）当t=13.5时，L＝22.5km
　（10）11点24分或13点32分距离家22千米.
9、设这批货成本为a元，月初出售到月末可获利润P₁=1000+(a+1000)×1.5%=0.015a+1015 ,　　月末出售可获利润P₂=1200-50=1150元 ,　P₁-P₂=0.015(a-9000)
　　故为a>9000时，月初出售好； 当a=9000时，月初，月末出售相同；
　　当a<9000时，月末出售好.

10、设周长为P，当r=h=时，闸板面积最大.
11、抛物线解析式为y=x²±2x+1.
设把抛物线y=x²±2x+1向下平称l个单位后，使∠ACB=60°，则平移后抛物线的解析式为y=x²±2x+1+l.　　

设A、B两点的横坐标分别为 C点纵坐标为，则按题意有①
　　又因此.　.
　　　代入①，得=1-l.　　 　平方，整理得(1-l)(l+2)=0.
　　因平移后抛物线仍保持同x轴有两个交点，所以x₁-x₂=≠0，即1-l≠0.
　　可得l+2=0，即l=-2.
　　于是可知，把已知抛物线向下平移2个单位，就能使∠ACB=60°.  解略.

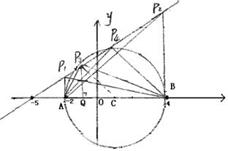12、（1）分三种情况：
　　① 若点A为直角顶点，P₁(-2,).
　　② 若点B为直角顶点， P₂(4,).　　

③ 若点P为直角顶点，P₃(), P₄(1,3).
　　综上P点坐标为P₁(-2,), P₂(4,),P₃(), P₄(1,3).
　　（2）设过A、B、P三点的抛物线的解析式为：y=a(x+2)(x-4)，将P₃，P₄代入，

　　 y= 或 y=.

13、连接OD、OE、OC，应证明OD⊥OC，OE⊥CD，

∴ RtΔODE∽RtΔCOE　 ∴ AD·BC=DE·CE=OE²=R².

14、①S₁+S₂=a². 　　 　　②OD⊥OF.

15、设BP=x，△APD的面积为　y= x²+x.
　　∴ x=2，即P为BC中点时，△APD的面积最大.