栖霞区2006年初三中考模拟试卷（一）
数 学
本试卷分第一卷（选择题）和第二卷（非选择题）两部分，第一卷从第1页至第2页，第二卷从第2页至第8页．全卷满分120分，考试时间120分钟．
第一卷（选择题 共24分）
一、选择题（每小题2分，共24分）
1．如果a与－2互为倒数，那么a是（ ）．
A．-2
B．-
C．
D．2
2．南京长江三桥是世界上第一座弧线形钢塔斜拉桥，全长15600m，用科学记数法表示为（ ）．
A．1.56×104m B．15.6×103 m C．0.156×104m D．1.6×104m
3．不等式组
的解集为（ ）．
A．x＞2 B．x＜3 C．x＞2或 x＜－3 D．2＜x＜3
4．若反比例函数
的图象经过点A（2，m），则m的值是（ ）．
A．
B．
C．
D．
5．一个袋中装有1个红球，2个白球，3个黄球，它们除颜色外完全相同．小明从袋中任意摸出1个球，摸出的是白球的概率是（ ）．
A．
B．
C．
D．1
6．已知α为等边三角形的一个内角，则cosα等于（ ）．
A．
B．
C．
D．
7．下列美丽的图案，既是轴对称图形又是中心对称图形的个数是（ ）．
 |
A．1个 B．2个 C．3个 D．4个
8．教练组对运动员正式比赛前的5次训练成绩进行分析，判断谁的成绩更加稳定，一般需要考察这5次成绩的（ ）．
A．平均数或中位数 B．众数或频率
C．方差或极差 D．频数或众数
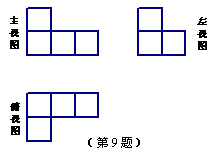
9．如图，是一个由若干个相同的小正方体组成的几何体的三视图，则组成这个几何体的小正方体的个数是（ ）．
A．4个 B．5个
C．6个 D．7个
10．根据下列表格的对应值：
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | －0.06 | －0.02 | 0.03 | 0.09 |
判断方程ax2+bx+c＝0（a≠0，a，b，c为常数）一个解x的范围是（ ）．
A．3＜x＜3.23 B．3.23＜x＜3.24
C．3.24＜x＜3.25 D．3.25＜x＜3.26
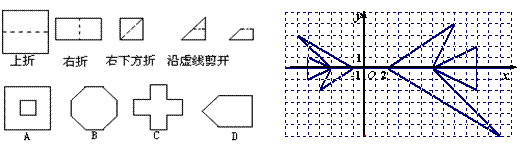
11．如图所示，把一个正方形三次对折后沿虚线剪下，则所得的图形是（ ）．
 |
|
|
12．某学习小组在讨论“变化的鱼”时，知道右图中的大鱼与小鱼是位似图形，若小鱼上的点P（a，b）对应大鱼上的点Q，则点Q的坐标为（ ）．
A．（－2a，－2b） B．（－a，－2b）
C．（－2b，－2a） D．（－2a，－b）
题号 | 一 | 二 | 三 | 四 | 五 | 六 | 七 | 八 | 合计 |
| 得分 | |||||||||
| 评卷人 |
第二卷（非选择题 共96分）
| 得分 | 评卷人 |
二、填空题（每小题3分，共12分）
13．比较大小：（1）－3 －4；（2）
．
14．用字母表示图中阴影部分的面积为 ．
15．某商店销售一批服装，每件售价150元，打8折后，仍可获利20%，设这种服装的成本价为
元，则x满足的方程是
．
16．用两块大小相同的等腰直角三角形纸片做拼图游戏，则下列图形：①平行四边形（不包括矩形、菱形、正方形）；②矩形（不包括正方形）；③正方形；④等边三角形；⑤等腰直角三角形，其中一定能拼成的图形是 ．
（只填序号）
| 得分 | 评卷人 |
三、解下列各题（每小题6分，共24分）
17．先化简，再求值：
，其中m＝－2．
18．解方程组：
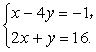
19．解不等式
，并把它的解集在数轴上表示出来．
20．如图，正方形ABCD的边CD在正方形ECGF的边CE上，连结BE、DG．
（1）观察猜想BE与DG之间的大小关系，并证明你的结论．
（2）图中是否存在通过旋转能够互相重合的两个三角形？若存在，请说出旋转过程；若不存在，请说明理由．
| 得分 | 评卷人 |
四、（每小题6分，共12分）
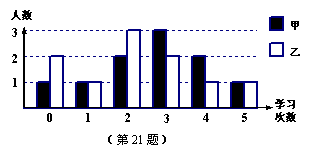
21．为了了解本地区中学生开展研究性学习的情况，抽查了某中学九年级甲、乙两班的部分学生，了解他们在一个月内参加研究性学习的情况，结果统计如下：
（1）在这次抽查中甲班被抽查了 人，乙班被抽查了 人；
（2）在被抽查的学生中，甲班学生参加研究性学习的平均次数为 次，乙班学生参加研究性学习的平均次数为 次；
（3）根据以上信息，用你学过的统计知识，推测甲、乙两班在开展研究性学习方面哪个班级更好一些？
（4）从图中你还能得到哪些信息？（写出一个即可）
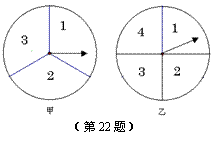22．同时转动如图所示的甲、乙两个转盘，求两个转盘所转到的两个数字之和为偶数的概率（用树状图或列表法分析求解）．
| 得分 | 评卷人 |
五、（每小题7分，共14分）
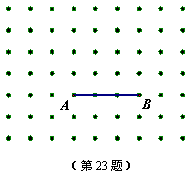
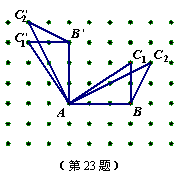
23．如图是9×7的正方形点阵，其水平方向和竖直方向相邻的两格点间的长度都是1个单位，以这些点为顶点的三角形称为网格三角形．请通过画图分析、探究回答下列问题：
（1）请在图中画出以AB为边且面积为3的一个网格三角形（记为△ABC）；
（2）将你所画的三角形绕着点A沿逆时针方向旋转90°，画出旋转后的图形（记为△AB′C′）．
 |
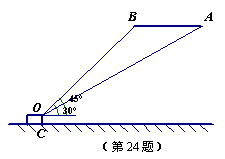24．如图，一架飞机以每小时900千米的速度水平飞行，某个时刻，从地面控制塔O（塔高300m）观测到飞机在A处的仰角为30°，5分钟后测得飞机在B处的仰角为45°，试确定飞机的飞行高度．（
，结果精确到1km）
| 得分 | 评卷人 |
六、（第25题7分，第26题8分，共15分）
25．如图，△ABC内部有若干个点，用这些点以及△ABC的顶点A，B，C把原三角形分割成一些三角形（互相不重叠）．
（1）填写下表：
| △ABC内点的个数 | 1 | 2 | 3 | 4 |
| 分割成的三角形的个数 | 3 | 5 |
（2）如果用y表示内部有n个点时，△ABC被分割成的三角形的个数，试写出y与n的关系式；
（3）原△ABC能否被分割成2006个三角形？若能，求此时△ABC内部有多少个点？若不能，请说明理由．
26．某校科技夏令营的学生在3位老师的带领下，准备赴北京大学参观，体验大学生活．现有两家旅行社前来洽谈，报价均为每人2000元，且各有优惠．希望旅行社表示：带队老师免费，学生按8折收费；青春旅行社表示师生一律按7折收费．经核算发现，参加两家旅行社的实际费用正好相等．
（1）该校参加科技夏令营的学生共有多少人？
（2）如果又增加了部分学生，学校应选择哪家旅行社？为什么？
| 得分 | 评卷人 |
七、（本题8分）
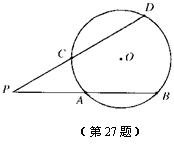
27．我们知道：顶点在圆上，并且两边都和圆相交的角叫做圆周角，一条弧所对的圆周角的度数等于它所对的圆心角度数的一半．类似地，我们定义：顶点在圆外，并且两边都和圆相交的角叫做圆外角．
（1）判断：图中有没有圆外角？如果有，请用字母表示出来．
（2）运用所学的数学知识，探究：圆外角的度数与它所夹的弧所对的圆心角的度数有什么关系？将你的发现，用文字表述出来，并说明理由．
 |
| 得分 | 评卷人 |
八、（本题11分）
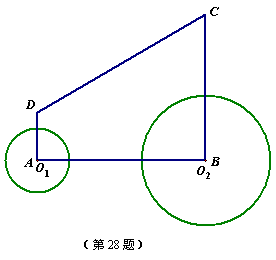
28．如图，直角梯形ABCD中，AD∥BC，∠A＝90o，∠C＝60°，AD＝3cm，BC＝9cm．⊙O1的圆心O1从点A开始沿折线A—D—C以1cm/s的速度向点C运动，⊙O2的圆心O2从点B开始沿BA边以
cm/s的速度向点A运动，⊙O1半径为2cm，⊙O2的半径为4cm，若O1、O2分别从点A、点B同时出发，运动的时间为ts
（1）请求出⊙O2与腰CD相切时t的值；
（2）在0s＜t≤3s范围内，当t为何值时，⊙O1与⊙O2外切？
2006年初三中考模拟试卷（一）参考答案及评分标准
一、选择题（每小题2分，共24分）
BADCB ACCBC CA
二、填空题（每小题3分，共12分）
13．＞，＞ 14．
15．150×80%－x＝20%x 16．①、③、⑤
三、解下列各题（每小题6分，共24分）
17．解：
………………2分
＝
………………3分
＝
．………………4分
当m＝－2时，原式＝
．………………6分
18．解：由①，得x＝4y－1．③………………1分
把③代入②，得2(4y－1)+y＝16．………………2分
解得y＝2．………………4分
把y＝2代入③，得x＝7．………………5分
所以原方程组的解为
………………6分
19．解：不等式两边同乘以6，得
2x－3(x－1) ≤6．………………2分
解这个不等式，得x≥－3………………4分
数轴表示正确．………………6分
20．解：（1）BE＝DG．………………1分
证明：∵四边形ABCD和四边形ECGF都是正方形，
∴BC＝DC，EC＝GC，∠BCE＝∠DCG＝90°．………………3分
∴△BCE≌△DCG．………………4分
∴BE＝DG．
（2）存在，它们是Rt△BCE和Rt△DCG．将Rt△BCE绕点C顺时针旋转90°，可与Rt△DCG完全重合．………………6分
四、（每小题6分，共12分）
21．（1）10人，10人；………………2分
（2）2.7次，2.2次；………………4分
（3）甲班学生参加研究性学习的平均次数大于乙班学生参加研究性学习的平均次数，所以在开展研究性学习方面甲班更好一些………………5分
（4）答案合理．………………6分
22．解：画树状图或列表正确．………………3分
两个转盘所转到的两个数字之和为偶数的概率为．………………6分
五、（每小题7分，共14分）
23．解：开放性试题，答案可参照右图，答案不惟一．
（1）所画△ABC符合要求；………………3分
（2）所画△AB′C′符合要求（如△ABC画错，旋转作图正确，得3分）．……7分
24．解：AB＝
＝75（km）．………1分
过点O作OD⊥AB，垂足为D．………………2分
设OD＝xkm，在Rt△OBD中，∵∠OBD＝45°，
∴BD＝OD＝xkm．……………3分
在Rt△OAD中，AD＝AB+ BD＝(x+75) km，∠AOD＝60°，
∵tan∠AOD＝
，∴
．………………5分
解得x≈102.5（km）．
∴CD＝ OD +OC ＝102.5+0.3≈103（km）．………………6分
答：飞机的飞行高度约为103 km．………………7分
六、（第25题7分，第26题8分，共15分）
25．解：（1）填表：………………2分
| △ABC内点的个数 | 1 | 2 | 3 | 4 |
| 分割成的三角形的个数 | 3 | 5 | 7 | 9 |
（2）y＝2n+1．………………4分
（3）若△ABC能被分割成2006个三角形，则2n+1＝2006．………………5分
，不是整数．………………6分
所以，原三角形不能被分割成2006个三角形．………………7分
26．解：（1）设共有学生x人，希望旅行社费用为y1元，青春旅行社费用为y2元．
……………1分
根据题意得：
，即
；
，即
．
当y1＝y2时，即1600x＝1400x＋4200，………………4分
解得x＝21．………………5分
所以该校参加科技夏令营的学生共有21人．………………6分
（2）y1－y2＝200 x－4200．当x＞21时，y1－y2＞0，即y1＞y2．
所以如果增加部分学生，学校应选择青春旅行社．………………8分
七、（本题8分）
27．解：（1）∠DPB是圆外角；………………1分
（2）圆外角的度数等于它所夹的弧所对的圆心角的度数的差的一半．………………4分
理由如下：连结DA，OA，OB，OC，OD，则
∵∠BAD＝∠BOD，∠ADC＝∠AOC，
∴∠BAD－∠ADC＝∠BOD－∠AOC．………………6分
∵∠DPB＝∠BAD－∠ADC，∴∠DPB＝∠BOD－∠AOC．………………8分
八、（本题11分）
28．解：（1）如图所示，设点O2运动到点E处时，⊙O2与腰CD相切．
过点E作EF⊥DC，垂足为F，则EF＝4cm．………………1分
方法一，作EG∥BC，交DC于G，作GH⊥BC，垂足为H．
通过解直角三角形，求得EB＝GH＝
cm．………………4分
所以t＝（
）秒．………………5分
方法二，延长EA、FD交于点P．通过相似三角形，也可求出EB长．
方法三，连结ED、EC，根据面积关系，列出含有t的方程，直接求t．
（2）由于0s<t≤3s，所以，点O1在边AD上．………………6分
如图所示，连结O1O2，则O1O2＝6cm．………………7分
由勾股定理得，
，即
．………………9分
解得t1＝3，t2＝6（不合题意，舍去）．………………10分
所以，经过3秒，⊙O1与⊙O2外切．………………11分
 |