前海学校05-06学年第二学期期中考试九年级试题
数 学
命题人：袁志刚
（时量：90分钟；满分：100分）
HI，亲爱的同学，你好！今天是展示你才能的时候了，只要你仔细审题、认真答题，把平常的水平发挥出来，你就会有出色的表现，放松一点，相信自己的实力！
一、选择题：（本大题共10题，每小题3分，共30分）
每小题给出四个答案，其中只有一个符合题目的要求，请把选出的答案编号填在下面的答题表一内，否则不给分.
答题表一
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
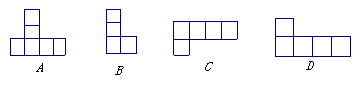
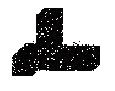1、右边几何体的俯视图是( )
2、下列计算正确的是（ ）
A、x2·x3＝x6 B、(2a3)2＝4a6 C、(a－1)2＝a2－1 D、＝±2
3、我国对农村义务教育阶段贫困家庭的学生实行“两免一补”政策，2005年至2007年三年内国家财政将安排约227亿元资金用于“两免一补”，这项资金用科学记数法表示为（ ）
A、2.27
元 B 227
元 C 22.7 元 D
2.27
元
4、若一元二次方程
有两个不相等的实数根x1、x2，且满足
，则m的值是（ ）
A 
B 
C 
D2
5、下列各式中，由左边到右边的变形是因式分解且正确的是（ ）
A.
B.
C.
D.
6、下列事件中，是必然事件的是（ ）
A、打开电视机，正在播放篮球比赛。
B、从一副扑克牌中任意抽出一张牌，花色是方块。
C、在同一年出生的367名学生中，至少有两人的生日是同一天.
D、掷一枚六个面分别标有1~6的数字的均匀骰子，骰子停止转动后朝上的点数正好是6。
7、下列图形中，既是轴对称图形，又是中心对称的图形是（ ）
A.
B．
C．
D．
8、、若点（
）、
、
都在反比例函数
的图象上，则
的大小关系是（ ）
A 
B 
C 
D 
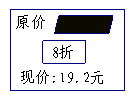
9、右图是“东方”超市中“飘柔”洗发水的价格标签，
一服务员不小心将墨水滴在标签上，使得原价看不
清楚，请帮忙算一算，该洗发水的原价（ ）
A.22元 B.23元 C.24元 D.26元
10、如图，OAB是以6cm为半径的扇形，AC切弧AB于点A交
OB的延长线于点C,如果弧AB的长等于3cm,AC=4cm,则图中阴
影部分的面积为（ ）
A.15cm2 B.6 cm2 C. 4 cm2 D. 3 cm2
二、填空题：（本大题共5小题，每小题3分，共15分，请将答案填入答题表二内，否则不给分）
答题表二
| 题号 | 11 | 12 | 13 | 14 | 15 |
| 答案 |
11、为了解中学生的身体发育情况，对某中学同年龄的60名同学的身高进行了测量．经统计，身高在148．5～151．5之间的频数为3，则这一组的频率为 ．
12、已知二次函数
的图象交x轴于A、B两点，在x轴上方的抛物线上存在一点C，且△ABC的面积为10，则C点的坐标为____________.
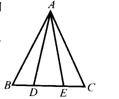
13、如图，已知D，E是∆ABC中BC边上的两点，AD=AE，
请你再附加一个条件____________，使∆ABE≌∆ACD。
14、观察下列顺序排列的等式：
9×0+1=1；9×1+2=11;9×2+3=21;9×3+4=31；9×4+5=41
猜想：第n个等式（n为正整数）应为________________。
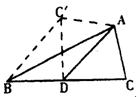
15、如图，AD是△ABC的中线，∠ADC=450，把△ADC沿
AD对折，点C落在C/的位置，则BC/与BC之间的数量
关系是_________。
三、解答题：（共7题，共55分）
解答应写出文字说明、证明过程或演算步骤.请你一定要注意噢！
16、（6分）计算：
17、（6分）先化简，后求值，其中：
，其中
。
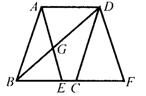18、（8分）如图，已知E是平行四边形ABCD的边BC上的
一点， F是BC延长线上一点，且BE=CF，BD与AE相
交于点G。
求证：（1）∆ABE≌∆DCF；
（2）BE·DF＝BF·GE。
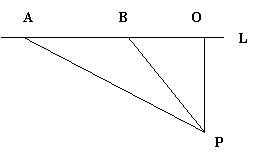19、（8分）如图，已知测速站P到公路L的距离PO为40米，一辆汽车在公路L上行驶，测得此车从点A行驶到点B所用的时间为2秒，并测得∠APO=600，∠BPO=300，计算此车从A到B的平均速度为每秒多少米（结果保留四个有效数字），并判断此车是否超过了每秒22米的限制速度。
20、（9分）某电视台在黄金时段的2分钟广告时间内，计划插播长度为15秒和30秒的两种广告。15秒广告每播1次收费0.6万元,30秒广告每播1次收费1万元。若要求每种广告播放不少于2次。问
（1）两种广告的播放次数有几种安排方式？
（2）电视台选择哪种方式播放收益较大？
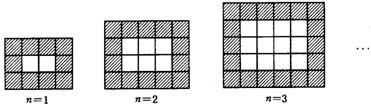
21、如图，用同样规格黑白两色的正方形瓷砖铺设矩形地面．请观察下列图形并解答有关问题：
⑴ 在第n个图中，每一横行共有 块瓷砖，每一坚列共有 块瓷砖（均用含n的代数式表示）；
⑵ 设铺设地面所用瓷砖的总块数为y，请写出y与（1）中的n的函数关系式（不要求写自变量n的取值范围）；
⑶ 按上述铺设方案，铺一块这样的矩形地面共用了506块瓷砖，求此时n的值；
⑷ 若黑瓷砖每块4元，白瓷砖每块3元，在问题⑶中，共需花多少元钱购买瓷砖？
⑸ 是否存在黑瓷砖与白瓷砖块数相等的情形？请通过计算说明为什么？
22、如图12，在矩形ABCD中，AB=12厘米，BC=6厘米．点P沿AB边从点A开始向点B以2厘米/秒的速度移动；点Q沿DA边从点D开始向点A以1厘米/秒的速度移动．如果P、Q同时出发，用t(秒)表示移动的时间(0≤t≤6),那么：
（1）当t为何值时，
为等腰直角三角形？
（2）求四边形
的面积；提出一个与计算结果有关的结论；
（3）当t为何值时，以点Q、A、P为顶点的三角形与
相 似？