2002年全国初中数学竞赛试题
(2002年4月7日上午 9:30——11:30)
一、选择题(每小题5分,共30分)
1、设a<b<0,a2+b2=4ab,则![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、2 D、3
C、2 D、3
2、已知a=1999x+2000,b=1999x+2001,c=1999x+2002,
则多项式a2+b2+c2-ab-bc-ca的值为( )
A、0 B、1 C、2 D、3
3、如图,点E、F分别是矩形ABCD的边AB、BC的中点,连AF、CE交于点G,
 则
则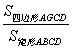 等于( )
等于( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、设a、b、c为实数,x=a2-2b+![]() ,y=b2-2c+
,y=b2-2c+![]() ,z=c2-2a+
,z=c2-2a+![]() ,
,
则x、y、z中至少有一个值( )
A、大于0 B、等于0 C、不大于0 D、小于0
5、设关于x的方程ax2+(a+2)x+9a=0,有两个不等的实数根x1、x2,
且x1<1<x2,那么a的取值范围是( )
A、![]() <a<
<a<![]() B、a>
B、a>![]() C、a<
C、a<![]() D、
D、![]() <a<0
<a<0
6、A1A2A3…A9是一个正九边形,A1A2=a,A1A3=b,则A1A5等于( )
 A、
A、![]() B、
B、![]() C、
C、![]() D、a+b
D、a+b
二、填空题(每小题5分,共30分)
7、设x1、x2是关于x的一元二次方程x2+ax+a=2的两个实数根,
则(x1-2x2)(x2-2x1)的最大值为 。
8、已知a、b为抛物线y=(x-c)(x-c-d)-2与x轴交点的横坐标,
 a<b,则
a<b,则![]() 的值为
。
的值为
。
9、如图,在△ABC中,∠ABC=600,点P是△ABC内的一点,
使得∠APB=∠BPC=∠CPA,且PA=8,PC=6,则PB= 。
10、如图,大圆O的直径AB=acm,分别以OA、OA为直径作
⊙O1、⊙O2,并在⊙O与⊙O1和⊙O2的空隙间作两个等圆⊙O3和⊙O4,
这些圆互相内切或外切,则四边形O1O2O3O4的面积为 cm2。
11、满足(n2-n-1)n+2=1的整数n有 个。
12、某商品的标价比成本高p%,当该商品降价出售时,为了不亏本,售价的折扣(即降价的百分数)不得超过d%,则d可以用p表示为 。
三、解答题(每小题20分,共60分)
13、某项工程,如果由甲、乙两队承包,![]() 天完成,需付180000元;由乙、丙两队承包,
天完成,需付180000元;由乙、丙两队承包,![]() 天完成,需付150000元;由甲、丙两队承包,
天完成,需付150000元;由甲、丙两队承包,![]() 天完成,需付160000元。现在工程由一个队单独承包,在保证一周完成的前提下,哪个队的承包费用最少?
天完成,需付160000元。现在工程由一个队单独承包,在保证一周完成的前提下,哪个队的承包费用最少?
 14、如图,圆内接六边形ABCDEF满足AB=CD=EF,且对角线AD、BE、CF交于一点Q,设AD与CE的交点为P。
14、如图,圆内接六边形ABCDEF满足AB=CD=EF,且对角线AD、BE、CF交于一点Q,设AD与CE的交点为P。
(1)求证:![]() (2)求证:
(2)求证:![]()
15、如果对一切x的整数值,x的二次三项式ax2+bx+c的值都是平方数(即整数的平方)。
证明:(1)2a、2b、c都是整数;
(2)a、b、c都是整数,并且c是平方数;反过来,如果(2)成立,是否对一切的x的整数值,x 的二次三项式ax2+bx+c的值都是平方数?