第十六届中国数学奥林匹克 (2001年)

1. 给定a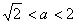， 。 内接于单位圆ABCD的凸四边形适合以下条件：
1. 圆心在这凸四边形内部；
2. 最大边长是a , 最小边长是 。

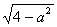过点A、B、C、D 依次作圆Γ 的四条切线L_A、L_B、L_C、L_D。已知 L_A与L_B、L_B与L_C、L_C与L_D、L_D与L_A分别相交于A' 、B' 、C' 、D' 四点。 求面积之比S_A'B'C'D' /S_ABCD的最大值与最小值。

2. 设X={1,2,3, … 2001}, 求最小的正整数m，适合要求：对X的任何一个m元子集W, 都存在u、v　( u和v允许相同 )，使得u+v是2的方幂。
3. 在正n边形的每个顶点上各停有一只喜鹊。偶受惊吓， 众喜鹊都飞去。 一段时间后，它们又都回到这些顶点上，仍是每个顶点上一只，但未必都回到原来的顶点。 求所有正整数n，使得一定存在3只喜鹊，以它们前后所在的顶点分别形成的三角形或同为锐角三角形，或同为直角三角形，或同为钝角三角形
4. 设a, b, c, a+b-c, a+c-b, b+c-a, a+b+c是7个两两不同的质数, 且a, b, c中有两数之和是800。设d 是这7个质数中最大数与最小数之差。求d的最大可能值。
5. 将周长为24的圆周等分成24段。 从24个分点中选取8个点，使得其中任何两点间所夹的弧长都不等于3和8。问满足要求的8点组的不同取法共有多少种？说明理由。
6. 记a=2001。设A是适合下列条件的正整数对(m，n)所组成的集合：
1. m < 2a；
2. 2n (2am-m²+n²)；
3.  n²-m²+2mn≦2a(n-m)。

令 ， 求 和 。