椒江育英学校第三次月考数学试题 命题人 龙清华
全卷共三大题，满分150分.考试时间120分钟
一. 选择题（本题有12小题，共48分．每小题只有一个选项是正确的，不选、多选、错选均不给分）
1．（泰山）如图所示的正四棱锥的俯视图是 ( )
 |
2（嘉兴）方程
的解是
( )
A、－2，2 B、0，－2 C、 0，2 D、0，－2，2
3.（四川内江）用12根火柴棒（等长）拼成一个三角形，火柴棒不允许剩余、重叠和折断，则能摆出不同的三角形的个数是 （ ）
A、1 B、2 C、3 D、4
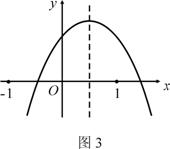
4（四川资阳）已知二次函数y=ax2+bx+c(a≠0)的图象如图3所示，给出以下结论
① a+b+c<0；② a-b+c<0；③ b+2a<0；④ abc>0 其中所有正确结论的序号 （ ）
A. ③④ B. ②③ C. ①④ D. ①②③
5.（泰山）两圆的半径R、r分别是方程x2－5x＋6=0的两根，且圆心距d =3，则两圆的位置关系为 ( )
A．外切 B．内切 C．外离 D．相交
6、（四川内江）一个密闭不透明的盒子里有若干个白球，在不允许将球倒出来的情况下，为估计白球的个数，小刚向其中放入8个黑球，摇匀后从中随机摸出一个球记下颜色，再把它放回盒中，不断重复，共摸球400次，其中88次摸到黑球，估计盒中大约有白球 （ ）
A、28个 B、30个 C、36个 D、42个
7（四川）已知正比例函数y=k1x(k1≠0)与反比例函数y=
(k2≠0)的图象有一个交点的坐标为(-2，-1)，则它的另一个交点的坐标是 （ ）
A. (2，1) B. (-2，-1) C. (-2，1) D. (2，-1)
8（四川）在一个地球仪的赤道上用铁丝打一个箍，现将铁丝箍半径增大1米，需增加ｍ米长的铁丝，假设地球的赤道上也有一个铁箍，同样半径增大1米，需增加ｎ米长的铁丝，则ｍ与ｎ的大小关系是 （ ）
A、ｍ＞ｎ B、ｍ＜ｎ C、ｍ＝ｎ D、不能确定
9（江苏） 电影院呈阶梯或下坡形状的主要原因是 ( ).
A.为了美观 B.盲区不变 C.增大盲区 D.减小盲区
10（四川内江）以上说法合理的是 （ ）
A、小明在10次抛图钉的试验中发现3次钉尖朝上，由此他说钉尖朝上的概率是30%
B、抛掷一枚普通的正六面体骰子，出现6的概率是1/6的意思是每6次就有1次
掷得6。
C、某彩票的中奖机会是2%，那么如果买100张彩票一定会有2张中奖。
D、在一次课堂进行的试验中，甲、乙两组同学估计硬币落地后，正面朝上的概率分别为0.48和0.51。
11、(2005浙江)根据下列表格的对应值：
| x | 3.23 | 3.24 | 3.25 | 3.26 |
|
| －0.06 | －0.02 | 0.03 | 0.09 |
判断方程
(a≠0，a，b，c为常数)一个解x的范围是 （ ）
A、3＜x＜3.23 B、3.23＜x＜3.24 C、3.24＜x＜3.25 D、3.25 ＜x＜3.26
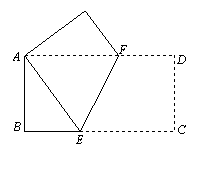12（江苏宿迁）如图，将一个边长分别为4、8的长方形纸片ABCD折叠，使C点与A点重合，则折痕EF的长是
（ ）
A．
B．
C．
D．
二、填空题（本大题共8小题，每小题4分，共32分，）
1.(2005余姚)某种商品原价50元.因销售不畅,3月份降价10%,从4月份开始涨价,5月份的售价为64.8元,则4、5月份两个月平均涨价率为 .
2.（泰山）在边长为3㎝、4㎝、5㎝的三角形白铁皮上剪下一个最大的圆，此圆的半径为____ ㎝.
3.（江西）收音机刻度盘的波长
和频率
分别是用米（m）和千赫兹（kHz）为单位标刻的。波长和频率满足关系式
，这说明波长越大，频率就越_________ ；
4．（广东茂名）用一个平面去截一个正方体其截面形状不可能的
是 （请你在三角形、四边形、五边形、六边形、七边形这五种图择符合题意的图形填上即可）；
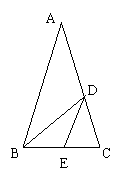
5（嘉兴）顶角为36°的等腰三角形称为黄金三角形，如 图，△ABC、△BDC、
△DEC都是黄金三角,已知AB=1，则DE=___________________
6．如图10，在⊙O中，已知∠ACB=∠CDB=60°，AC=3，则⊙O的半径是 ．
 |
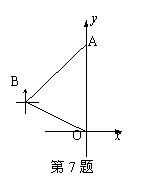7. (泰州市) 如图，机器人从A点沿着西南方向，行了4个单位，到达B点后观察到原点O在它的南偏东60°的方向上，则原来A的坐标为
（结果保留根号）．
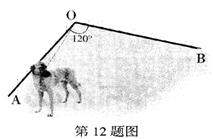
8．（宁德）如图，墙OA、OB的夹角ÐAOB＝120º，OA=7m。OB=9m，一根9m长的绳子一端栓在墙角
O处，另一端栓着一只小狗，则小狗可活动的区域的面积是 m2（结果保留π）。
三、解答题（写出必要的解题步骤）
1．（十堰市）（8分）
如图:已知△ABC中，BD.CE是△ABC的高。请你增加一个条件，写出一个结论，并证明你写出的结论。
增加的条件为：
已知：
求证：
证明:
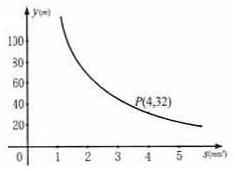
2（济南市8分）、你吃过拉面吗？实际上在做拉面的过程中就渗透着数学知识：一定体积的面团做成拉面，面条的总长度y(m)是面条的粗细(横截面积)s(mm2)的反比例函数，其图象如图所示。
⑴写出y与s的函数关系式；
⑵求当面条粗1.6mm2时，面条的总长度是多少米？
 |
3. 山东省青岛市（本小题满分10分）
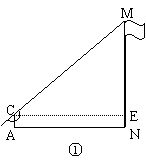
在一次实践活动中，某课题学习小组用测倾器、皮尺测量旗杆的高度，他们设计了如下方案（如图①所示）：
(1)在测点A处安置测倾器，测得旗杆顶部M的仰角∠MCE=α;
(2)量出测点A到旗杆底部N的水平距离AN=
;
(3)量出测倾器的高度AC=
.
根据上述测量数据，即可求出旗杆的高度MN.
如果测量工具不变，请仿照上述过程，设计一个测量某小山高度（如图②）的方案：
(1)在图②中，画出你测量小山高度MN的示意图（标上适当字母）；
(2)写出你设计的方案.
 |
4。（泰山 10分）如图，AB切⊙O于点B，OA交⊙O于C点，过C作DC⊥OA交AB于D，且BD：AD=1：2
（1）求∠A的正切值.（4分）
（2）若OC =1，求AB及 BC的长.（6分）
5（河北10分） 某食品零售店为仪器厂代销一种面包，未售出的面包可退回厂家，以统计销售情况发现，当这种面包的单价定为7角时，每天卖出160个。在此基础上，这种面包的单价每提高1角时，该零售店每天就会少卖出20个。考虑了所有因素后该零售店每个面包的成本是5角。
设这种面包的单价为x（角），零售店每天销售这种面包所获得的利润为y（角）。
⑴用含x的代数式分别表示出每个面包的利润与每天卖出的面包个数；
每个面包的利润为 角，每天卖出的面包个数为
⑵求y与x之间的函数关系式；
⑶当面包单价定为多少时，该零售店每天销售这种面包获得的利润最大？最大利润为多少？
6．（内江市 10分）小红和小明在操场做游戏，他们先在地上画了半径分别2ｍ和3ｍ的同心圆（如图），蒙上眼在一定距离外向圈内掷小石子，掷中阴影小红胜，否则小明胜，未掷入圈内不算，你来当裁判。
⑴你认为游戏公平吗？为什么？
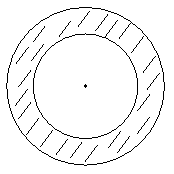⑵游戏结束，小明边走边想，“反过来，能否用频率估计概率的方法，来估算非规则图形的面积呢？”。请你设计方案，解决这一问题。（要求画出图形，说明设计步骤、原理，写出公式）
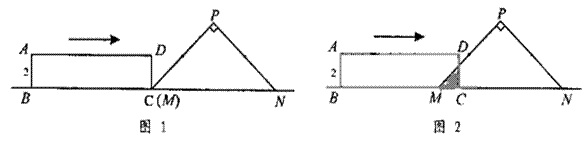
7．（河南课改 14分）如图1，Rt△PMN中，∠P＝90°，PM＝PN，MN＝8cm，矩形ABCD的长和宽分别为8cm和2cm，C点和M点重合，BC和MN在一条直线上。令Rt△PMN不动，矩形ABCD沿MN所在直线向右以每秒1cm的速度移动（如图2），直到C点与N点重合为止。设移动x秒后，矩形ABCD与△PMN重叠部分的面积为y
。求y与x之间的函数关系式。
