九年级上综合题（2）
姓名________ 座号______ 得分____
一． 选择题（每题2分，共20分）
1.下列性质中正方形具有而菱形没有的是（ ）
A.对角线互相平分 B.对角线相等
C.对角线互相垂直 D.一条对角线平分一组对角
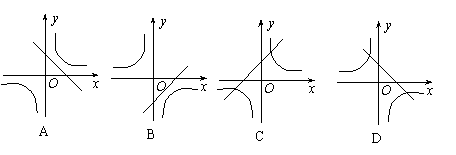
2.在同一直角坐标系中，函数y=kx-k与
(k≠0)的图象大致是（ ）
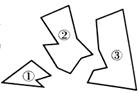
3.下面四幅图是两个物体不同时刻在太阳光下的影子，按照时间的先后顺序正确的是（ ）
A.A→B→C→D B. D→B→C→A C. C→D→A→B D. A→C→B→D
4.有一实物如图，那么它的主视图 （ ）
 |
5.设M表示直角三角形，N表示等腰三角形，P表示等边三角形，Q表示等腰直角三角形，则下列能表示它们之间关系的是（ ）
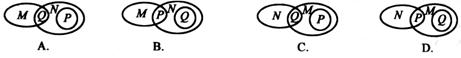
6.下列说法正确的有（ ）个
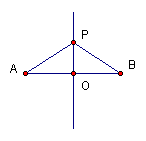
（1） 如下图，已知PA＝PB，则PO是线段AB的垂直平分线；
（2）
对于反比例函数
，（x1,y1）,（x2,y2）是其图象上两点，若x1<x2,则y1>y2；
（3） 对角线互相垂直平分的四边形菱形；
（4） 如下图，在△ABC中，∠A＝30°BC=2，则AC＝4;
（5）
一组对边平行的四边形是梯形；
（6）
是反比例函数；
（7）若一个等腰三角形的两边长为2和3,那么它的周长为7.
A.0 B.1 C.2 D.5
7.如图，某同学不慎将一块三角形玻璃打碎成了三块，现在要到玻璃店去配一块完全一样的玻璃，那么最省事的办法是（ ）
A.带①去 B.带②去 C.带①和②去 D.带③去
(7题图) (8题图) (9题图)
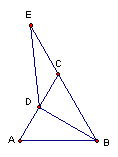
8.如图，D是等边三角形ABC中AC边的中点，E在BC的延长线上，DE＝DB，若
△ABC的周长为6,则△BDE的周长和面积为（ ）
A.
B.
C.
D.
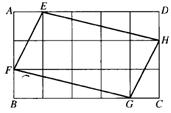
9.如图，将矩形ABCD分成15个大小相等的正方形，E、F、G、H分别在AD、AB、BC、CD边上，且是某个小正方形的顶点.若四边形EFGH的面积为1,则矩形ABCD的面积是（ ）
A.2
B.
C.
D.
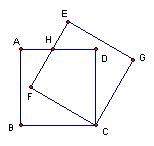
10.如图，△ABP与△CDP是两个全等的等边三角形，且PA⊥PD.有下列四个结论：①∠PBC＝15°;②AD∥BC；③直线PC与AB垂直；④四边形ABCD是轴对称图形.其中正确的结论的个数为（ ）
A.1 B.2 C.3 D.4
 | |||
 | |||
(10题图) (11题图) (12题图)
二．填空题（每空2分，共20分）
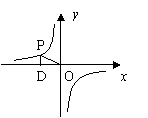
11.如图，点P是反比例函数
上的一点，PD⊥
轴于点D，则△POD的面积为
;
12.如图，边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFGH，EF交AD于点H，那么DH的长为________;
13.命题“等腰三角形两底角的平分线相等”的逆命题是______________________________________;
14.一元二次方程
有根的k的取值范围是________________;
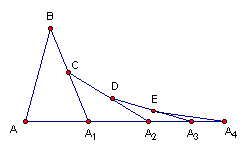15.如图，已知
∠B＝20°，则∠
＝_____;
 |  | ||
(15题图) (17题图) (18题图)
16.一菱形的对角线长分别为24cm和10cm，则此菱形的周长为___________，面积为____________；
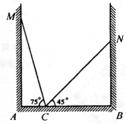
17.如图，在一个房间内，有一个梯子斜靠在墙上，梯子顶端距地面的垂直距离MA＝5米，此时梯子的倾斜角为75°.如果梯子底端不动，顶端靠在对面墙上，此时梯子顶端距地面的垂直距离NB为4米，梯子的倾斜角为45°.则这间房子的宽AB是________米；
18.如图5，在立方体ABCD－A1B1C1D1中，连接AB1、AC、B1C，则△AB1C的形状是_______三角形；
19.扑克牌游戏 小明背对小亮，让小亮按下列四个步骤操作：
第一步 分发左、中、右三堆牌，每堆牌不少于两张，且各堆牌现有的张数相同；
第二步 从左边一堆拿出两张，放入中间一堆；
第三步 从右边一堆拿出一张，放入中间一堆；
第四步 左边一堆有几张牌，就从中间一堆拿几张牌放入左边一堆.这时，小明准确说出了中间一堆牌现有的张数.你认为中间一堆牌现有的张数是 .
三． 解方程（每题4分，共8分）
20.
21.
四． 作图题（每题5分，共10分）
22.确定图中路灯灯泡的位置，并画出小赵在灯光下的影子；
23.在下面指定位置画出此实物图的三种视图.
 |
五． 解答、证明题（每题8分，共24分）
24.如图，已知E为平行四边形ABCD中DC边的延长线的一点，且CE＝DC，连接AE，分别交BC、BD于点F、G，连接AC交BD于O，连接OF.求证：AB＝2OF.
25.正比例函数
和反比例函数的图象相交于A，B两点，已知点A的横坐标为1,点B的纵坐标为－3.
（1） 求A，B两点的坐标；
（2） 写出这两个函数的表达式.
26.已知：如图，矩形AOBC，以O为坐标原点，OB，OA分别在x轴，y轴上，点A坐标为（0,3），∠OAB＝60°,以AB为轴对折后，使C点落在D点处，求D点的坐标.
六． 探索题（第1题，每空1分，共2分；第2题4分；第3题6分；第4题，每空3分，共6分；此题共18分）
27.探索一个问题：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”（完成下列空格）
1.
当已知矩形A的边长分别为4和1时，小明是这样研究的：设所求矩形的两边分别是
，由题意得方程组：
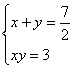，消去y化简得：
∵△＝49－48>0 ∴
∴满足要求的矩形B存在.
2. 如果已知矩形A的边长分别为2和1，请你仿照小明的方法研究是否存在满足要求的矩形B.
3. 如果矩形A的边长为m和n，请你研究满足什么条件时，矩形B存在？
4. 如图，在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象，其中x和y分别表示矩形B的两边长，请你结合刚才的研究，回答下列问题：
（1） 这个图象所研究的矩形A的两边长为_____和_____;
（2） 
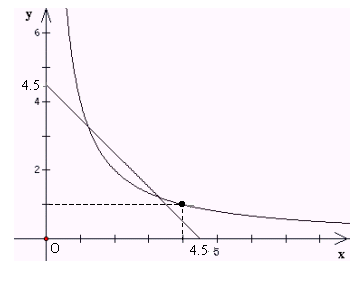满足条件的矩形B的两边长为_____和_____.