九年级上综合题（3）

姓名________  座号______　得分____

一．填空题（10×3′）

1.　　　 用计算器计算:sin20°≈_______(保留四个有效数字)；

若cosa=0.168,则a的度数为_____　__(精确到秒)。

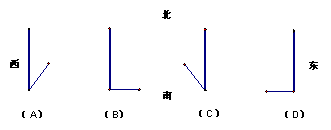
2.　　　 如图中(A)(B)(C)(D)中是一天中四个不同时刻的木杆在地面上的影子,将它们按时间先后顺序排列正确的一项是_______。

　　　　　　　　　

3.　　　 已知菱形的两条对角线分别为6cm和8cm,则这个菱形的面积为_______。

4.　　　 已知矩形的一条对角线把一个内角分为2:1,对角线长为8cm,则这个矩形的长边为______。

5.　　　 反比例函数y=的图象在第_______象限,在每个象限内,y的值随x的减小而______。

6.　　　 在同一坐标系中,函数y=mx的图象与函数y=的图象有交点,则mn______0；若没有交点则mn________0。

7.　　　 在⊿ABC中, ∠A, ∠B都是锐角,且，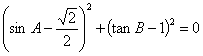

则△ABC是_________。

8.　　　 如图,BD是平行四边形ABCD的对角线,点E、F在BD上,要使四边形AECF是平行四边形,还需要增加的一个条件是_________(填上你认为正确的一个即可,不必考虑所有可能的情形)。

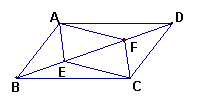
（8题图）　　　　　　　　　　　　　　　　　　 （10题图）

9.　　　 试写出一个开口向上,对称轴为直线x=2,并且与y轴交点坐标是(0,4)的抛物线的函数表达式_____________________________________。

10.　 某广场要做一个由若干盆花组成的形如正六边形的花坛,每条边(包括两个顶点)有n(n>1)盆花,设这个花坛边上的花盆的总数为S,请观察图中的规律:按上规律推断,S与n的关系是________________

二.选择题.(10×2′)

11.　 正方形具有而菱形不具有的性质是(　　  )。

(A)内角和360°　　　　　 (B)四个角都是直角

(C)两组对边分别相等　　　 (D)对角线平分对角

12.　 高4米的旗杆在水平地面上的影长5米,此时测得附近一个建筑物的影子长20米,则该建筑物的高是(　　　)。

(A)16米　　　 (B)20米　　　　(C)24米　　　  (D)30米

13.　 如果四边形的对角线相等,那么顺次连结这个四边形各边中点所得的四边形必定是(　　　)。

(A)梯形　　　 (B)矩形　　　　(C)菱形　　　　(D)正方形

14.　

y

y

y

y

函数与 (a≠0),在同一坐标系中的图象可能是如图中的(　　　)。

x

(A)　　　　　　  (B)　　　　 　　　 (C)　　　　　　  (D)

15.　 在Rt△ABC中, ∠C=∠Rt,AC=1,AB=.则∠B为(　　　)。

　 (A)30°　　　 (B)45°　　　 (C)60°　　　  (D)90°

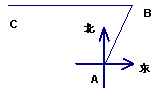
16.　 如图在Rt△ABC中, ∠ACB=90°,CD⊥AB，D为垂足，若AC=4,BC=3，则sin∠ACD的值为(　　 )。

(A) 　　　 (B) 　　　 (C) 　　　　(D)

（16题图）　　　　　　　　　 （18题图）　　　　　　  （19题图）

17.　 若是反比例函数，且它们的图象在第二，四象限，则n的值是（　　 ）。

(A) 0　　　　 (B) 1　　　　(C)1或0　　　(D)非上述答案

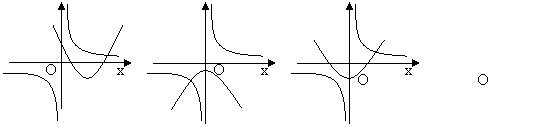
18.　 在如图的函数中，当x>0时,y随x的增大而减小的是(　　 )。

　 (A)y=2x　　　 (B)y=2x-1　　(C)y=-　  (D)y=-2

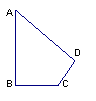
19.　 如图,从A地沿北偏东30°方向走100m,到B地再从B地向西走200m到C地,这时小明离A地(　　  ) 。

(A) 150m　　　(B)100 m　(C) 100m　　(D) 50 m

20.　 某块绿地的形状如图,其中∠A=60°,AB⊥BC,AD⊥CD,AB=200m,CD=100m,则BC的长为 (　　 ) 。

(A) m (B)m (C)m (D)m

三.解答题

21.　 计算　　 °°°　　　　 (5′)

22.　 画出下图中物体的三种视图。(5′)

23.　 楼房,旗杆在路灯下的影子如图所示,画出小树在路灯下的影子。(5′)

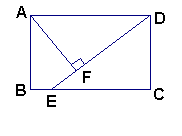
24.　 已知如图,在矩形ABCD中,E为BC上的一点,且DE=BC,AF⊥DE于点F,求证:EF=BE(5′)

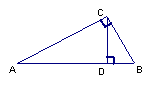
25.　 如图,河对岸有铁塔AB,在C处测得塔顶A的仰角为30°,向塔前进14米到达D,在D处测得A的仰角为45°,求铁塔AB的高。(6′)

26.　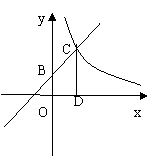 如图,已知一次函数的图象与x轴、y轴分别交于A、B两点,且与反比例函数的图象在第一象限交于C点,CD垂直与x轴,垂足为D.若OA=OB=OD=1,

（I）求点A，B，D的坐标；

	A

（II）求一次函数和反比例函数的解析式。（7′）

27.　 某高科技发展公司投资500万元，成功研制出一种市场需求量较大的高科技替代产品，并投入资金1500万元进行批量生产。已知生产每件产品的成本为40元。在销售过程中发现：到销售单价为100元时，年销售量为20万件；销售单价每增加10元，年销售量将减少1万件。设销售单价为x（元），年销售量为y（万件），年获利（年获利=年销售额-生产成本-投资）为z（万元）。

（1）　　　 试写出y与x之间的函数关系式（不必写出x的取值范围）；

（2）　　　 试写出z与x之间的函数关系式（不必写出x的取值范围）；

（3）　　　 计算销售单价为160元时的年获利，并说明同样的年获利，销售单价还可以定为多少元？相应的年销售量分别为多少万件？

（4）　　　 公司计划：在第一年按年获利最大确定的销售单价，进行销售；第二年年获利不低于1130万元。请你借助函数的大致图象说明，第二年的销售单价x（元）应确定在什么范围内？（10′）

28.　 已知抛物线的顶点M（2，2）与y轴交点（0，3），O是原点。

（1）　　　 求这条抛物线的函数解析式。

（2）　　　 问在x轴上是否存在点P使△OPM为等腰三角形？

若存在，把符合条件的P点坐标求出来；若不存在说明理由。（7′）

一．