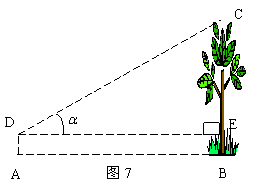 九年级数学阶段性测试
九年级数学阶段性测试
一、填空题(每题2分,共22分)
1、Rt△ABC中,∠C=90°,AC=3,AB=5,则sinB=_______。
2、已知∠A是锐角,cosA=![]() ,则sinA= ,tanA= 。
,则sinA= ,tanA= 。
3、等腰三角形中,腰长5,底边长8,则底角的正切值是
4、Rt△ABC中,![]() ,则
,则![]() ;
;
5、在△ABC中,![]() ,AC边上的中线BD=5,AB=8,则
,AC边上的中线BD=5,AB=8,则![]() =
=
6、已知![]() 是锐角,
是锐角,![]() ,则
,则![]() =_______度。
=_______度。
7、计算:![]() = 。
= 。
8、抛物线![]() 与y轴的交点坐标是 。
与y轴的交点坐标是 。
9、二次函数![]() 的顶点坐标为 ,对称轴是 ;
的顶点坐标为 ,对称轴是 ;
10、抛物线![]() ,当自变量
,当自变量![]() 时,该函数的函数值随
时,该函数的函数值随![]() 的增大而增大.
的增大而增大.
11、用长度一定的绳子围成一个矩形,如果矩形的一边长![]() (m)与面积
(m)与面积![]() (m
(m![]() )满足函数关系
)满足函数关系![]()
0<![]() <24 ,则该矩形面积的最大值为___
m
<24 ,则该矩形面积的最大值为___
m![]()
二、选择题(每小题2分,共16分)
12、![]() 中,如果各边长度都扩大2倍,则锐角
中,如果各边长度都扩大2倍,则锐角![]() 的三角函数值( )。
的三角函数值( )。
A.不变化 B.扩大2倍 C.缩小![]() D.不能确定
D.不能确定
13、在Rt△ABC中,已知![]() 边及∠A,则斜边应为( )。
边及∠A,则斜边应为( )。
A.![]() B.
B.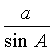 C.
C.![]() D.
D.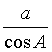
14、下列函数关系中,是二次函数的是( )。
A.在弹性限度内,弹簧的长度y与所挂物体质量x之间的关系;
B.当距离一定时,火车行驶的时间t与速度v之间的关系;
C.等边三角形的周长C与边长a之间的关系;
D.半圆面积S与半径R之间的关系。
 15、抛物线
15、抛物线![]() 可由抛物线
可由抛物线![]() ( )而得到。
( )而得到。
A.先向左平移2个单位,再向下平移1个单位;
B.先向左平移2个单位,再向上平移1个单位;
C.先向右平移2个单位,再向下平移1个单位;
D.先向右平移2个单位,再向上平移1个单位。
16、已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:① a+b+c<0;②![]() <0;③b+2a<0;④abc>0;⑤
<0;③b+2a<0;④abc>0;⑤![]()
其中所有正确结论的序号是( )
A.②③④ B.②③⑤ C.①④⑤ D.①②③
17、①![]() ②
② ![]()
③ ![]() ④
④ ![]()
其中,函数y的值随着x值得增大而减少的是( )
A.① B、② C、③ D、④
 18、已知抛物线
18、已知抛物线![]() 的部分图象如图所示,
的部分图象如图所示,
下列说法正确的是( )
A.![]() ; B.若y=0,则
; B.若y=0,则![]()
与x轴的交点是(-1,0),(3,0);
C.y随x的增大而减小的x的范围是:x>1;
D.若y![]() 0,则x取值范围是:x<-1或 x>3
0,则x取值范围是:x<-1或 x>3
19、小明、小亮、小梅、小花四人共同探讨代数式x2-4x+5的值的情况.他们作了如下分工:小明负责找其值为1时的x的值,小亮负责找其值为0时的x的值,小梅负责找最小值,小花负责找最大值,几分钟后,各自通报探究的结论,其中错误的是( )
A.小明认为只有当x=2时,x2-4x+5的值为1
B.小亮认为找不到实数x,使x2-4x+5的值为0
C.小梅发现x2-4x+5的值随x的变化而变化,因此认为没有最小值
D.小花发现当x取大于2的实数时,x2-4x+5的值随x的增大而增大,因此认为没有最大值
三、解答题(共62分)
![]() 20、计算:(6分)
20、计算:(6分)
![]() +
+![]() ·
·![]() ·
·![]()
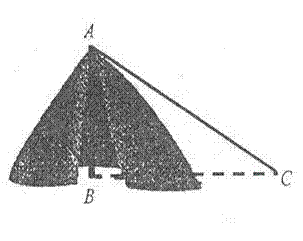 21、如图,从帐篷竖直的支撑竿AB的顶端A向地面拉出一条绳子AC固定帐篷.若地面固定点C到帐篷支撑竿底部B的距离是4.5米,∠ACB=30°,求帐篷支撑竿AB的高(结果保留根号).
21、如图,从帐篷竖直的支撑竿AB的顶端A向地面拉出一条绳子AC固定帐篷.若地面固定点C到帐篷支撑竿底部B的距离是4.5米,∠ACB=30°,求帐篷支撑竿AB的高(结果保留根号).
(8分)
 22、完成下表内的解答。(10分)
22、完成下表内的解答。(10分)
| 题目 | 测量底部可以到达的树木的高 | |||
| 测量 目标 |
| |||
| 测得 数据 | 测量项目 | AB的长 | 测倾器的高 | 倾斜角 |
| 第一次 | 30米 | AD |
| |
| 第二次 | 40米 | AD |
| |
|
计
算 | 求树高BC(精确到0.1米. 取平均值,可得这棵树的高大约是 米. 说说你对测量一个物体高度的看法:
| |||
 23、大楼AD的高为10米,远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60º,爬到楼顶D点测得塔顶B点的仰角为30º,求塔BC的高度。(8分)
23、大楼AD的高为10米,远处有一塔BC,某人在楼底A处测得塔顶B处的仰角为60º,爬到楼顶D点测得塔顶B点的仰角为30º,求塔BC的高度。(8分)
24、某商人如果将进货价为8元的商品按每件10元出售,每天可销售100件,现采用提高售价,减少进货量的办法增加利润,已知这种商品每涨价1元,其销售量就要减少10件,问他将售价定为多少元时,才能使每天所赚的利润最大?并求出最大利润.(8分)
25. (本题9分)
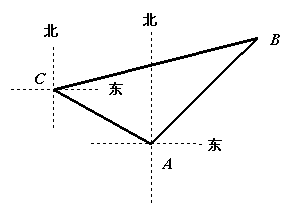
如图,甲、乙两只捕捞船同时从A港出海捕鱼. 甲船以每小时15![]() 千米的速度沿西偏北30
千米的速度沿西偏北30![]() 方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时后到达C处,此时甲船发现鱼具丢在乙船上,于是甲船快速(匀速)沿北偏东75
方向前进,乙船以每小时15千米的速度沿东北方向前进,甲船航行2小时后到达C处,此时甲船发现鱼具丢在乙船上,于是甲船快速(匀速)沿北偏东75![]() 的方向追赶,结果两船在B处相遇.(注:东北方向指东偏北45
的方向追赶,结果两船在B处相遇.(注:东北方向指东偏北45![]() )
)
(1)甲船从C处追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?
![]() 26、(13分)如图,在一块三角形区域ABC中,∠C=90°,边AC=8,BC=6,现要在△ABC内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上。
26、(13分)如图,在一块三角形区域ABC中,∠C=90°,边AC=8,BC=6,现要在△ABC内建造一个矩形水池DEFG,如图的设计方案是使DE在AB上。
(1)求△ABC中AB边上的高h;(3分)
(2)设DG=![]() ,则GF的长度如何表示;(3分)
,则GF的长度如何表示;(3分)
 (3)设水池DEFG的面积为
(3)设水池DEFG的面积为![]() ,当
,当![]() 取何值时,水池DEFG的面积最大?(4分)
取何值时,水池DEFG的面积最大?(4分)
 (4)实际施工时,发现在AB上距B点1.85的M处有一棵大树,问:这棵大树是否位于最大矩形水池的边上?如果在,为保护大树,请设计出另外的方案,使三角形区域中欲建的最大矩形水池能避开大树。(3分)
(4)实际施工时,发现在AB上距B点1.85的M处有一棵大树,问:这棵大树是否位于最大矩形水池的边上?如果在,为保护大树,请设计出另外的方案,使三角形区域中欲建的最大矩形水池能避开大树。(3分)