2006年初三数学模拟试卷
一、选择题（本大题共10小题，每小题4分，共40分）
1．下列运算正确的是 （ ）
A．x2+x2=x4 B。(a－1)2=a2－1 C。3x+2y=5xy D。a2·a3=a5
2．以下各图放置的小正方形的边长都相同，分别以小正方形的顶点为顶点画三角形，则
与△ABC相似的三角形图形为
（A） （B） （C） （D）
3．在0，－１，０．１，－０．２这四个数中，最小的数是 （ ）
Ａ．－１ Ｂ．０ Ｃ．－０．２ Ｄ．０．１
4．一批货物总重９．８×１０６kg，下列可将其一次性运走的合适运输工具是 （ ）
Ａ．一艘万吨巨轮 Ｂ．一架飞机 Ｃ．一辆汽车 Ｄ．一辆手拉车
5．小丽制作了一个如下左图所示的正方体礼品盒，其对面图案都相同，那么这个正方体的平面展开图可能是（ ）
 |
6．小明同学身高1。60米，晚上站在路灯下，他的身影长为2米，若沿影子的方向直走2米后站立，此时影子加长了0.5米，则路灯的高度是 （ ）
（A）6米 （B） 7米 （C） 7。2米 （D） 8米
7．计算机利用的是二进制数，它共有两个数码0、1，将一个十进制数转化为二进制数，只需要把该数写成若干个2n数的和，依次写出1或0即可. 如十进制数19=16＋2＋1=1×24＋0×23＋0×22＋1×21＋1×20, 转化为二进制数就是10011, 所以19是二进制下的5位数. 问：2005是二进制下的几位数( )
A. 10 B. 11 C. 12 D. 13
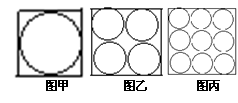8．如图，在三个同样大小的正方形中，分别画一个内切圆，面积为S1（图甲所示）；画四个半径相等的两两外切、且与正方形各边都相切的圆，这四个圆的面积之和为S4（图乙所示）；画九个半径相等相互外切、且与正方形各边都相切的圆，这九个圆的面积之和为S9（图丙所示）；则S1 、S4和S9的大小关系是
（A）S1最大 （B）S4最大
（C）S9最大 （D）一样大
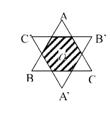
9．如图△ABC中，AB=BC=AC=3，O为它的内心，以O为中心将△ABC旋转1800得到△A/B/C/，则△ABC与△A/B/C/的重叠部分的面积为 （ ）
A．
B．
C．
D．6
10．某校的围墙上端由一段段相同的凹曲拱形栅栏组成，其中一段栅栏如图所示，其拱形图形为抛物线的一部分，栅栏的跨径ＡＢ间按相同的间距０．２米用５根立柱加固，拱高ＯＣ为０．６米，以Ｏ为原点，ＯＣ所在的直线为y轴建立平面直角坐标系，根据以上的数据，则这一段栅栏所需立柱的总长为（精确到０．１米 （ ）
Ａ．１．５米 Ｂ．１．９米 Ｃ．２．３米 Ｄ．２．５米
 |
二、填空题（本题共6小题，每小题5分，共30分）
11．如果2x－3的值为
，那么4x2－12x＋9的值是 。
12.观察下面一列数，按某种规律在横线上填入适当的数，并说明你的理由.
，
，
， ，
，…你的理由是_______________
13．将一副三角尺如图摆放一起,连接AD, 则∠ADB的余切值为 .
14．实数x1、x2满足｜x1－x2｜＝，则x1，x2的方差等于 。
15.形状是三角形ABC的绿化草地，∠B=30度，AB=20米，AC=25米。则这块三角形草地的面积 平方米。
16. 如图在L上依次摆7个正方形,斜的面积分
别为1, 2, 3, 正放置的四个正方形的面积依次
为S1, S2, S3, S4, 则S1+S2+S3+S4=_____.
三、解答题（本题共8小题，第17~18题每题8分，第21题10分，第22、23题每题12分，第24题14分，共80分）
17．化简：
·（x2－16）
18．现有四个代数式：x＋1，x－5，cos60°，2，请用它们构造出一个一元二次方程，并求其根（每个代数式都要用上，但只能用一次）。
19．作图题：在一节劳技课上，老师要求把一个直角一分为三，很多同学都很为难，只有小明很快做好了，你知道他是怎么做的吗？请你试着把它画出来。
20．为了普及环保知识，增强环抱知识，某中学组织了环保知识竞赛活动，初中三个年级根据初赛成绩分别选出了10名同学参加决赛（满分为100分）如下表所示：
| 决赛成绩（单位：分） | |
| 七年级 | 80 86 88 80 88 99 80 74 91 89 |
| 八年级 | 85 85 87 97 85 76 88 77 87 88 |
| 九年级 | 82 80 78 78 81 96 97 88 89 86 |
（1）请你填写下表：
| 平均数 | 众数 | 中位数 | |
| 七年级 | 85．5 | 87 | |
| 八年级 | 85．5 | 85 | |
| 九年级 | 84 |
（2）请从以下两个不同的角度对三个年级的决赛成绩进行分析：
①从平均数和众数相结合看（分析哪个年级成绩好些）：
②从平均数和中位数相结合看（分析哪个年级成绩好些）：
（3）如果在每个年级参加决赛的选手中分别选出3人参加总决赛，你认为哪个年级的实力更强一些？并说明理由：
21．阅读下列材料解答下列问题：观察下列方程：①x+
=3; ②x+
=5; ③x+
=7; …：
（1）按此规律写出关于x的第n个方程为 ；此方程的解为 。
（2）根据上述结论，求出x+
=2n+2 (n≥2)的解，并验根。
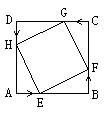
22．如图，正方形ABCD的边长为2cm，E、F、G、H分别从A、B、C、D向B、C、D、A同时以0.5cm/s的速度移动，设运动时间为t(s)。
（1）求证：△HAE
△EBF
（2）设四边形EFGH的面积为S（
），
求S与t的函数关系式，
并写出自变量t的取值范围。
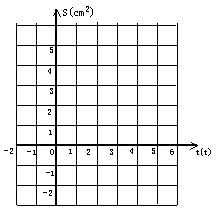
（3）画出（2）的图象，利用图象
回答t为何值时，S最小，是多少？
23．在如图的方格纸中（小方格的边长是1个单位）有一点O和△ABC。
(1)请以点O为位似中心，把△ABC缩小为原来的一半（不改变方向），得到
△A/B/C/。
(2)请用适当的方式描述△A/B/C/的顶点A/、B/、C/的位置。
24．如图，抛物线y=ax2＋bx＋c的顶点为A（4,4），且抛物线经过原点，和x轴相交于另一点B，以AB为一边在直线AB的右侧画正方形ABCD。
（1）求抛物线的解析式和点C、D的坐标。
（2）能否将此抛物线沿着直线x=4平移，使平移后的抛物线恰好经过正方形ABCD的另两个顶点C、D？若能，写出平移后抛物线的解析式，若不能，请说明理由。
（3）若以点A（4,4）为圆心，r为半径画圆。请你探究：
①当r= 时，圆A上有且只有一个点到直线BD的距离等于2；
②当r= 时，圆A上有且只有三个点到直线BD的距离等于2；
③随着r的变化，圆A上到直线BD的距离等于2的点的个数也随着变化，请根据圆A上到直线BD的距离等于2的点的个数，讨论相应的r的值或取值范围。
 |