2004--2005学年度第二学期九年级第三次质量调查

数学试题

第I卷（选择题 共30分）

一. 选择题：（本大题共10小题，每小题3分，共30分。在每小题给出四个选项中，只有一项是符合题目要求的。）

1. 第五次全国人口普查结果显示，我国的总人口已达到人，用科学记数法表示这个数，正确的是（ ）

A. B. C. D.

2. 为了了解某区2万名学生参加中考的情况，有关部门从中抽取了500名学生的成绩进行统计分析，在这个问题中（ ）

A. 2万名考生是总体 B. 每名考生是个体

C. 500名考生是总体的一个样本 D. 样本的容量是500

3. 若，则的值为（ ）

A. 1 B. C. 1或D. 0

4. 如图，，P为OA上的一点，且OP=5cm，若以P为圆心，为半径的圆与OB相切，则半径为（ ）

A. 5cm B. C. D.

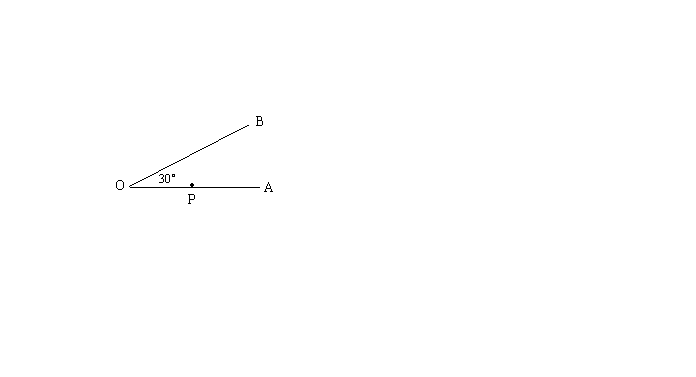
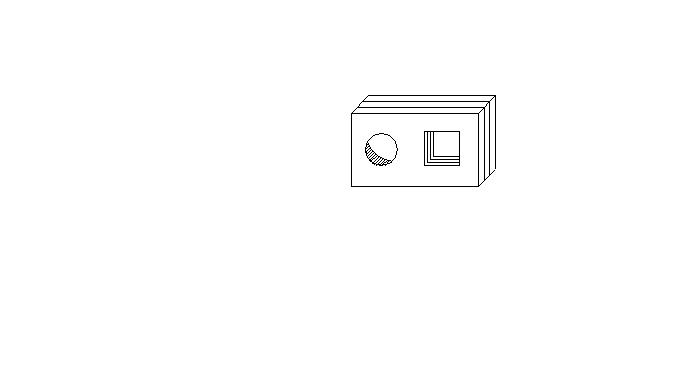
5. 如图是一块带有圆形空洞和方形空洞的小木板，则以下列物体作为塞子，既可以堵住圆形空洞又可以堵住方形空洞的是（ ）

A B C D

6. 若一个正九边形的边长为，则这个正九边形的半径是（ ）

A. B. C. D.

7. 下列语句或式子中正确的是（ ）

A. 任何实数的零次幂都等于1 B. 5的倒数的相反数是

C. D. 若，则

8. 如图，中，于D，BE⊥AC于E，AD与BE相交于F，若BF=AC，那么的大小是（ ）

A. 40° B. 45° C. 50° D. 60°

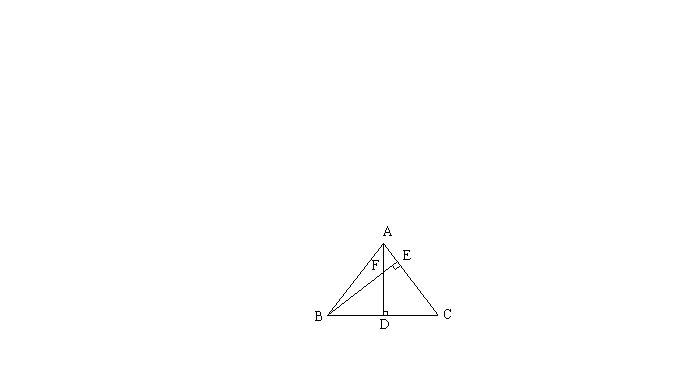
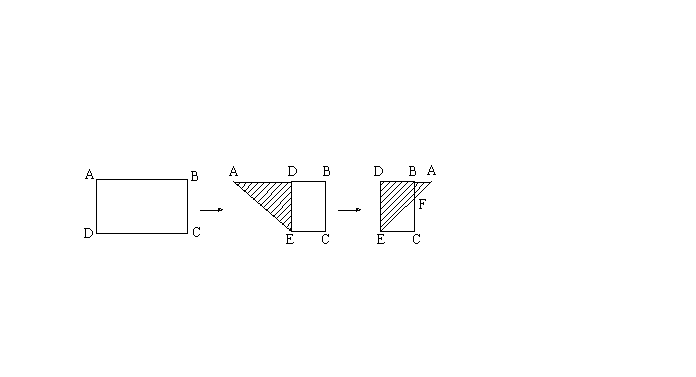
9. 如图，有一矩形纸片ABCD，AB=10，AD=6，将纸片折叠，使AD边落在AB边上，折痕为AE，再将以DE为折痕向右折叠，AE与BC交于点F，则梯形BDEF的面积为（）

A. 14 B. 16 C. 18 D. 10

10. 如图，半圆O的直径AB=4，与半圆O内切的动圆O₁与AB切于点M，设圆O₁的半径为，AM的长为，则关于的函数关系式是（ ）

A. B. C. D.

第II卷（非选择题 共90分）

二. 填空题：本大题共8小题，每小题3分，共24分，请将答案直接填在题中横线上。

11. 当且时，化简。

12. 在1000个数据中，用适当的方法抽取50个作为样本进行统计，频率分布表中54.5~57.5这一组的频率是0.12，那么估计总体数据落在54.5~57.5之间的有 个。

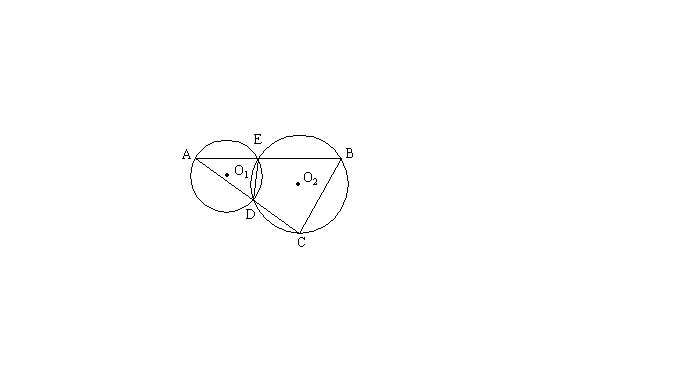
13. 如图，⊙O₁与⊙O₂相交于D、E两点，A是⊙O₁上一点，AE的延长线和AD的延长线分别交⊙O₂于B、C，DE=2，AC=12，BC=6，则AE= 。

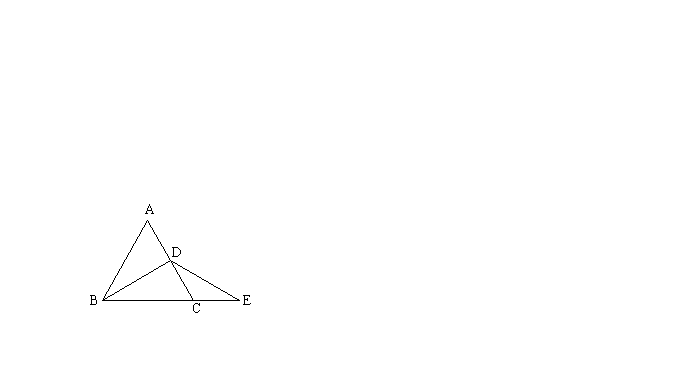
14. 如图，等边三角形ABC的周长为6cm，其中BD是中线，且，E为BC延长线上一点，，则的周长为 cm。

15. 若一次函数与轴交点的纵坐标为，且与两轴围成的直角三角形的面积为1，则。

16. 如图，已知AB是圆O的弦，AC是圆O的切线，的平分线交圆O于D，连BD并延长交AC于点C，若，则度。

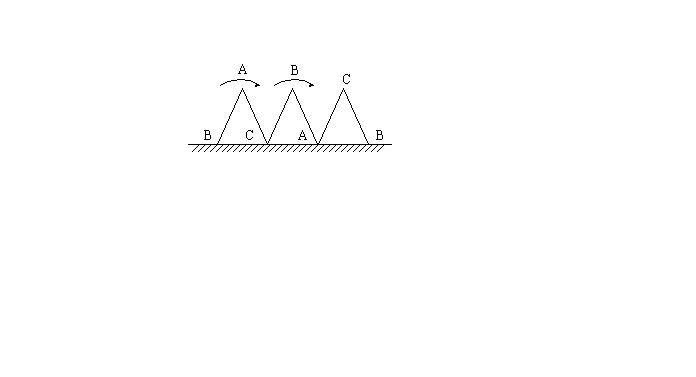
17. 一块等边三角形的木板，边长为1，现将木板沿水平线翻滚（如图），那么B点从开始至结束所走过的路径长度为 。

18. 已知二次函数与轴交点的横坐标为、（），则对于下列结论：① 当时，；② 当时，；③ 方程

有两个不相等的实数根、；④ ，；⑤ ，其中所有正确的结论是 （只需填写序号）。

三. 解答题：本大题共8小题，共66分。解答应写出文字说明、演算步骤或证明过程。

19.（本小题6分）

求使方程组的解、都是正数的m的取值范围。

20.（本小题8分）

某校餐厅计划购买12张餐桌和一批餐椅，现从甲、乙两商场了解到；同一型号的餐桌报价每张均为200元，餐椅报价每张均为50元，甲商场称：每购买一张餐桌赠送一把餐椅；乙商场规定：所有餐桌椅均按报价的八五折销售，那么，什么情况下到甲商场购买更优惠。

21.（本小题8分）

已知，如图所示，的斜边OA在轴正半轴上，直角顶点在第一象限，OA=5，OB=。

（1）求A、B两点的坐标；

（2）求经过O、B、A三点且对称轴平行于轴的抛物线的解析式，并确定抛物线顶点的坐标。

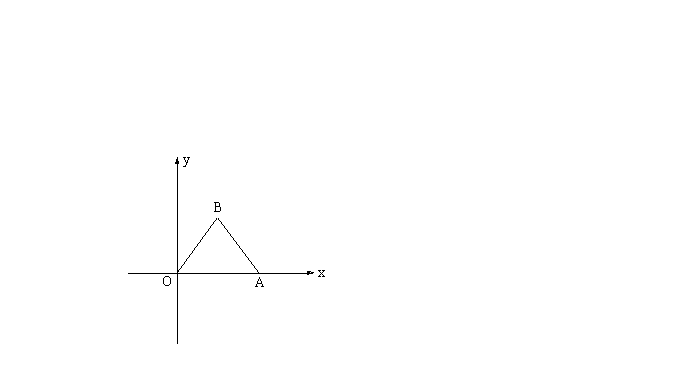
22.（本小题8分）

已知：如图，⊙O₁和⊙O₂外切于点A，直线BD切⊙O₁于点B，交⊙O₂于点C、D。直线DA交⊙O₁于点E。

（1）求证：；

（2）求证：。

23.（本小题8分）

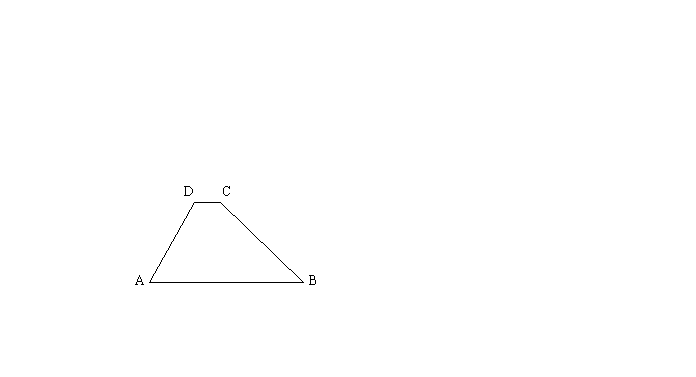
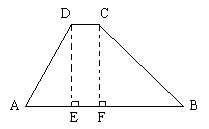
如图，某一水库大坝的横断面是梯形ABCD，坝顶宽CD=3cm，斜坡AD=16cm，坝高8m，斜坡BC的坡度，求斜坡AD的坡角和坝底宽AB。

24.（本小题8分）

某工厂计划生产300吨化工原料，生产6天后，改进了流程，提高了生产效率，每天比改进前多生产2吨，结果提前4天完成计划，问改进前每天生产化工原料多少吨？

25.（本小题10分）

已知：如图，⊙O₁和⊙O₂相交于点A、B，过点A的直线分别交⊙O₁、⊙O₂于C、D，E为上一点，直线BE交⊙O₂于点F，交AC于点G。

（1）求证：CE∥FD；

（2）若E为的中点，求证：；

（3）在（2）的条件下，当等于多少时，有，请说明理由。

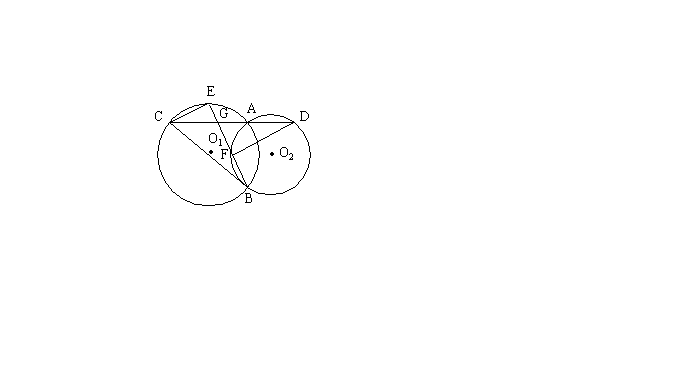
26.（本小题10分）

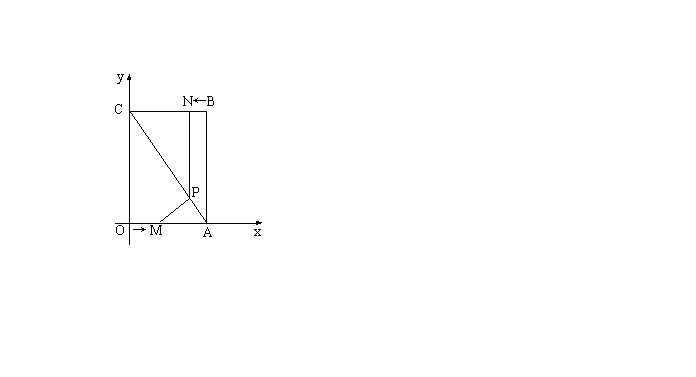
如图，平面直角坐标系中，四边形OABC为矩形，点A、B的坐标分别为（3，0）、（3，4），动点M、N分别从O、B同时出发，以每秒1个单位的速度运动。其中，点M沿OA向终点A运动，点N沿BC向终点C运动。过点N作NP⊥BC，交AC于点P，连结MP。已知动点运动了秒。

（1）P点的坐标为（ ， ）；（用含的代数式表示）。

（2）试求面积的最大值，并求此时的值；

（3）请你探索：当为何值时，是一个等腰三角形？你发现了几种情况？写出你的研究成果。

2004�2005学年度第二学期九年级第三次质量调查

数学试题参考答案及评分标准

一. 选择题（本大题共10小题，每小题3分，共30分）

1. B 2. D 3. B 4. C 5. B 6. D 7. C 8. C 9. B 10. C

二. 填空题（本大题共8小题，每小题3分，共24分）

11. 12. 120 13. 4 14. 15. 16. 17.

18. ①③④

三. 解答题：

19. 解：

原方程组得（3分）

∵ 它的解为正数 ∴ ∴

∴

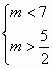
∴ 当时，原方程组的解都是正数（6分）

20. 解：设学校计划购买把餐椅，到甲、乙两商场购买所需费用分别为、，根据题意得：

，即：（3分）

，即：（6分）

当时，

∴

即：当购买的餐椅少于32把时，到甲市场购买更优惠（8分）

21. 解：

（1）∵ OA在轴上，且OA=5，∴ A点坐标为（5，0）（1分）

过B作BD⊥OA于D，则

∴ ，（3分）

在中，由勾股定理，得

∴ B点坐标为（1，2）（4分）

（2）因为抛物线经过O（0，0）A（5，0）两点

∴ 可设其解析式为（5分）

又 ∵ 抛物线经过点B（1，2）

∴ 得

故所求抛物线解析式为

即（7分）

∴ 抛物线的顶点坐标为（，）（8分）

22.

（1）证明：过A点作⊙O₁和⊙O₂的公切线MN（1分）

则（1分）

∵ CB是⊙O₁的切线 ∴ （3分）

∴ （4分）

（2）证明：连结BE，则（5分）

又 ∵

∴ （6分）

∴ （7分）

即（8分）

23. 解：分别过D、C点向AB作垂线，E、F是垂足（1分）

∵ 坝高为8m，∴ DE=CF=8 ∵ 斜坡BC的坡度

∴ （3分）

在中，∵

∴ （4分）

在中，（5分）

∵ ，∴ （6分）

∴ AB=AE+EF+BF=AE+DC+BF=（7分）

答：斜坡AD的坡角等于，坝底宽AB等于（8分）

24. 设改进前每天生产化工原料吨，则改进后每天生产化工原料吨。依题意得

（4分）

解得，（6分）

经检验，都是原方程的根，但不合题意，舍去

答：改进前每天生产化工原料10吨。（8分）

25.

（1）证明：连结AB

∵ ，∴

∴ CE∥FD（2分）

（2）∵ ∴

又 ∵ ∴ （4分）

（3）当时，有（5分）

证明如下：

∵ CE∥FD，∴

∴ ①（7分）

又 ∵ ∴ ②（9分）

①×②，得：，即（10分）

26.

（1）（，）

（2）设的面积为S，

在中，MA=，MA边上的高为，其中，

∴

∴ S的最大值为。此时（4分）

（3）延长NP交轴于Q，则有PQ⊥OA

① 若MP=PA ∵ PQ⊥MA ∴ MQ=QA=∴ ∴ （6分）

② 若MP=MA，则MQ=，，PM=MA=

在中，∵

∴ ∴ （8分）

③ 若PA=AM ∵ PA=，AM=∴ ∴

综上所述，，或，或（10分）