分类讨论

一. 本周教学内容： 分类讨论

［复习目标］

　　通过本单元练习卷的解答，使学生进一步了解分类讨论的思想方法，从而培养学生严密的逻辑推理能力和良好的思维品质。

［解题要领］

　　在解答习题时，往往需要按某一标准把问题分成若干部分或情况，分别加以研究逐一解之，从而得到清楚完整的结果，这种解题思想就是分类讨论。分类要注意两点：（1）正确选择一个分类标准；（2）分类要科学，既不重复，又不遗漏。分类讨论的试题在最近几年的中考卷中占有一定的比例，且往往作为压轴、难题出现，对能力要求较高，如绍兴03年的最后一题。请同学们细细体会。

一. 填空题（每空4分，共40分）

　1. 直角三角形中，已知两边的长分别为3cm和4cm，则第三边长为_________cm。

　2. 已知，则__________。

　3. 已知⊙与⊙相切，半径分别为2cm和5cm，则__________cm。

　4. 等腰三角形的两边长分别为4cm，9cm，则此等腰三角形的周长为__________cm。

　5. 若实数a，b，满足条件，则__________。

　6. 若等腰三角形腰上的高线等于腰长的一半，则其顶角为__________度。

　7. 在半径为5cm的圆中有一条弦的长度为，则此弦所对的圆周角的度数等于__________度。

　8. 已知，则____________________。

　9. △ABC的一个外角等于40°，若，则∠C＝__________度。

　10. 平面上两点A，B到直线的距离分别是，则线段AB的中点M到直线的距离是____________________。

二. 解答题（第11～15题每题10分，第16～20题，每题12分，共110分）

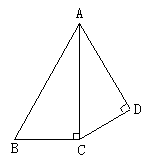
　11. 如图，在两个直角三角形中，∠ACB＝∠ADC＝Rt∠，，，问：当AB取何值时，这两个直角三角形相似？

　12. 已知：，问：直线一定通过什么象限？

　13. 如图，在直角坐标系中，点A（2，0）在x轴上，点P（x，2）在第一象限，当x取何值时，△POA为等腰三角形？

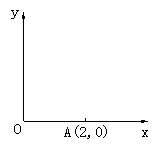
　14. 如图，一条公路途径A，B，C三个村庄，现在决定在A，C间设一个停车站P，已知：AB＝10km，BC＝35km，记BP＝xkm，P到A，B，C三个村庄的路程之和是y km。

　　（1）写出y关于x的函数关系式；

　　（2）当停车站P设在何处时，P到三个村庄的总路程y不超过50km？

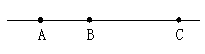
　15. 一项工程，若甲、乙两人独做分别需要6天，10天。如果允许两人合作，且要求两人各做整数天，那么如何派工可以使工期最短？最短工期是几天？

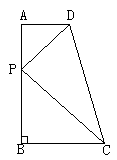
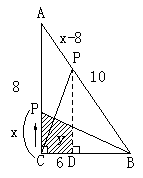
　16. 在直角梯形ABCD中，AD∥BC，AB⊥BC于B，且AD＝2，BC＝3，AB＝7。问在线段AB上是否存在点P，使得以P，A，D为顶点的三角形与以P，B，C为顶点的三角形相似？若不存在，说明理由；若存在，这样的P点有几个？并计算出AP的长度。

　17. 为美化环境，计划在某小区内用的草皮铺设一块边长为10m的等腰三角形绿地，请你求出这个等腰三角形绿地的另两边长。

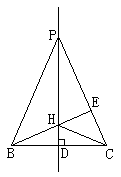
　18. 如图，直线是线段BC的中垂线，垂足为D，点P为上一动点（点P与点D不重合），连结PB，PC，作BE⊥PC于E。交于点H。问：当点P在上运动且与点D距离变小时，的值变小，变大，还是不变？提出你的猜想，并加以证明。

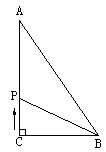
　19. 如果，中，∠ACB＝Rt∠，BC＝6cm，AC＝8cm，动点P从C点出发以1cm/秒的速度沿CA，AB运动到B。

　　（1）设P点运动的路程为xcm，△BCP的面积为，求y与x之间的函数关系式。

　　（2）从C点出发几秒钟时，△BCP的面积为△ABC的？

　20. 如图，已知抛物线与x轴交于A（1，0），B（3，0）两点，且过点（-1，16），抛物线的顶点是C点，对称轴与x轴交于D点，原点为O点。若y轴的正半轴上有一动点N，使以A，O，N三点为顶点的三角形与以C，A，D三点为顶点的三角形相似，

　　（1）求这条抛物线的解析式；

　　（2）求N点坐标。

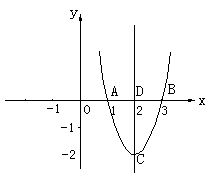
试题答案

一. 填空题。

  1. 5或　　　　　　　　　　　 2. 　　　　　　　　　　　　　　　　　 3. 7或3

  4. 22　　　　　　　　　　　　　　　　　 5. 2或　　　　　　　　　　　　　　6. 30或150

  7. 60或120　　　　　　　　　　　 8. 2或-2或0　　　　　　　　　　　　9. 140

  10. 或2

二. 解答题。

  11. 解：（1）若△ABC∽△ACD

　　则

　　

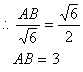
　　（2）若△ABC∽△CAD

　　则

　　

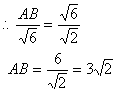
　　∴当AB＝3或时，△ABC与△ACD相似

  12. 解：（1）当时，由等比定理可得：

　　

　　（2）当时，

　　必过一、二、三象限

　　而必过二、三、四象限

　　一定通过二、三象限

  13. 解：∵△POA为等腰三角形

　　∴若以OP为底时，则P（2，-2）

　　　若以OA为底时，则P（1，2）

　　　若以AP为底时，则P为（0，2）

　　又∵P（x，2）在第一象限

　　或2时，△POA为等腰三角形

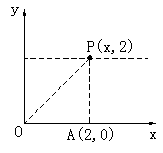
  14. 解：（1）当P在BC之间（包括B点）时，P到A、B、C三村的路程之和：

　　

　　当P在AB之间时，

　　（2）当时，即

　　∴当停车站P离B村庄不超过5km时，P到三个村庄的总路程y不超过50km

　15. 解：设甲独做x天，乙独做y天完成工程

　　则

　　

　　（）

　　当时，

　　∴让乙队做5天，甲队做3天可使工期最短，最短工期是5天

　16. 解：设AP长为x，则

　　（1）若△APD∽△BPC，有：

　　

　　

　　（2）若△APD∽△BCP，有：

　　

　　

　　∴这样的P点有3个，分别当AP长为1，6，时两三角形相似

　17. 解：分三种情况：

　　（1）若设，且为底时

　　过C作CD⊥AB于D

　　

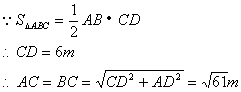
　　（2）若，且为腰的锐角三角形时

　　

　　（3）若，且为腰的钝角三角形时，

　　

　18. 解：猜想：当点P在上运动且与点D距离变小时，

　　的值不变

　　

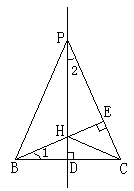
　　证：∵P是BC中垂线上的点

　　∴PB＝PC

　　又∵BE⊥PC

　　

　　

　　

　　

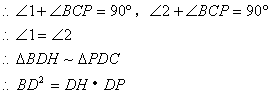
  19. 解：（1）当时，

　　

　　当时（过P作PD⊥BC于D）

　　

　　而△PDB∽△ACB

　  

　　

　　（2）

　　

　　∴当时，分别代入；

　　中，得：或

　　∴当x出发2秒或15.5秒时，

  20. 解：（1）设所求的抛物线为

　　把代入得：a＝2

　　∴解析式为：

　　（2）∵C点坐标为（2，-2）

　　

　　∴当△AON∽△ADC时，N点坐标为（0，2）

　　　当△AON∽△CDA时，N点坐标为（0，）