2006年福州市初三毕业班质量检查数学综合练习
一、 选择题
 1.图1中几何体的主视图是( )
1.图1中几何体的主视图是( )
2.2003年信息产业部的统计数据表明,截止到10月底,我国的电话用户总数达到5.12亿,居世界首位.其中5.12亿用科学记数法表示应为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.不等式组![]() 的解集是( )
的解集是( )
A.x>3 B.x<2 C.2<x<3 D.x>3 或x<2
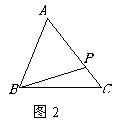 4.如图2,P是△ABC的边AC上的一点,连接BP,以下条件中不能判定△ABP∽△ACB的是( )
4.如图2,P是△ABC的边AC上的一点,连接BP,以下条件中不能判定△ABP∽△ACB的是( )
A. ![]() B.
B. ![]()
C.∠ABP=∠C D.∠APB=∠ABC
 5.点P(2,3)关于x轴的对称点为Q(m,n
),点Q关于Y轴的对称点为M(x,y),由点M关于原点的对称点是( )
5.点P(2,3)关于x轴的对称点为Q(m,n
),点Q关于Y轴的对称点为M(x,y),由点M关于原点的对称点是( )
A.(-2,3) B.(2,-3) C.(-2,-3) D.(2,3)
6.已知:a+b=m,ab=-4, 化简(a-2)(b-2)的结果是( )
A. 6 B. 2 m-8 C. 2 m D. -2 m
7.图3是小明制作的一个圆锥形纸帽的示意图.围成这个纸帽
的纸的高为( )cm2(π取3.14).
A.12; B.15; C.20; D.![]()
8.在比例尺为1:40000的工程示意图上,将于2005年9月1日正式通车的南京地铁一号线(奥体中心至迈皋桥段)的长度约为54.3cm,它的实际长度约为( )
A、0.2172km B、2.172km C、21.72km D、217.2km
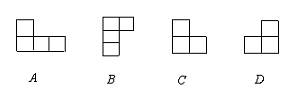
9、将一正方形纸片按图4中⑴、⑵的方式依次对折后,再沿⑶中的虚线裁剪,最后将⑷
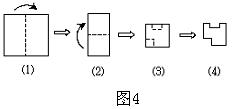
中的纸片打开铺平,所得图案应该是下面图案中的( )
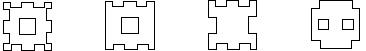
A B C D
10.一个口袋中有10个红球和若干个白球,请通过以下实验估计口袋中白球的个数:从口袋中随机摸出一球,记下其颜色,再把它放回口袋中,不断重复上述过程.实验中总共摸了200次,其中有50次摸到红球.估计口袋中白球的个数是( )
A.10; B.20; C.30; D.40
二、 填空题 www.czsx.com.cn
11.分解因式:5x+5y= .
12.如图5,将一张等腰直角三角形纸片沿中位线剪开,可以拼出不同形状的四边形,请写出其中两个不同的四边形的名称: 。

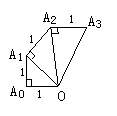
图5 图6 图7
13.如图6,已知,在△ABC和△DCB中,AC=DB,若不增加任何字母与辅助线,要使△ABC≌△DCB,则还需增加一个条件是_ _。
14.已知:![]() ,
,![]() ,
,![]() ,
,
……,若![]() (a、b都是正整数),则a+b的最小值是_ 。
(a、b都是正整数),则a+b的最小值是_ 。
15.如图7,该螺旋形由一系列直角三角形组成,则第n个三角形的面积为 。
三、 解答题
16、(1)计算:(![]() )0+(
)0+(![]() )-1-
)-1-![]() --1;
--1;
(2)解方程组![]()
(3)解不等式组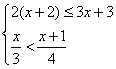 ,并写出不等式组的整数解。
,并写出不等式组的整数解。
17、先化简,再求值:(![]() )÷
)÷![]() ,其中x=2006;
,其中x=2006;
18.证明三角形中位线定理.
19.某商厦试销一种成本为50元/件的商品,规定试销时的销售单价不低于成本,又不高于80元/件,试销中销售量y(件)与销售单价x(元/件)的关系可近似的看作一次函数.
(1) 求y与x的关系式;
(2)设商厦获得的毛利润(毛利润=销售额-成本)为s(元),则销售单价定为多少时,该商厦获利最大?最大利润是多少?此时的销售量是多少件?

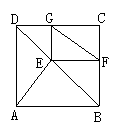
20.如图9,![]() 是正方形
是正方形![]() 的对角线
的对角线![]() 上一点,
上一点,![]() ,
,![]() ,垂足分别是
,垂足分别是![]() .求证:
.求证:![]() .
.
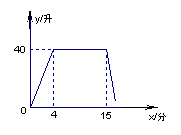
21.某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如图10所示。
请解答:
(1) 洗衣机的进水时间是多少分钟?清洗时洗衣机中的水量是多少升?
(2)已知洗衣机的排水速度为每分钟19升,求:
① 排水时y与x之间的关系式。
② 假设排水时间为2分钟,求排水结束时洗衣机中剩下的水量。
 |
22.已知线段AC=8,BD=6。
⑴已知线段AC垂直于线段BD。设图11-1、图11-2和图11-3中四边形ABCD的面积分别为S1、S2和S3,则S1= ,S2= ,S3= ;
⑵如图11-4,对于线段AC与线段BD垂直相交(垂足O不与点A,C,B,D重合)的任意情形,请你就四边形ABCD面积的大小提出猜想,并证明你的猜想;
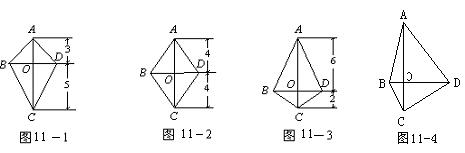 ⑶当线段BD与AC(或CA)的延工线垂直相交时,猜想顺次连接点A,B,C,D,A所围成的封闭图形的面积是多少?
⑶当线段BD与AC(或CA)的延工线垂直相交时,猜想顺次连接点A,B,C,D,A所围成的封闭图形的面积是多少?
23.在对某地区一次人口抽样统计中,各年龄段的人数如下表所示(年龄为整数)。请根据此表回答下列问题:
| 年龄 | 0~9 | 10~19 | 20~29 | 30~39 | 40~49 | 50~59 | 60~69 | 70~79 | 80~89 |
| 人数 | 9 | 11 | 17 | 18 | 17 | 12 | 8 | 6 | 2 |
(1)这次抽样的样本容量是________;
(2)在这个样本中,年龄的中位数位于哪个年龄段内_______;
(3)在这个样本中,年龄在60岁以上(含60岁)的频率是_______;
(4)如果该地区有人口80000,为关注人口老龄化问题,请估算该地区60岁以上(含60岁)的人口数。
24.如图,在平面直角坐标系中,O为坐标原点,点A是x轴的负半轴上一点,以AO为直径的⊙P经过点C(-8,4). 点E(m,n)在⊙P上,且-10<m≤—5,n<0,CE与x轴相交于点M,过C点作直线CN交x轴于点N,交⊙P于点F,使得△CMN是以MN为底的等腰三角形,经过E、F两点的直线与x轴相交于点Q.
(1)求出点A的坐标;
(2)当m=-5时,求图象经过E、Q两点的一次函数的解析式;
(3)当点E(m,n)在⊙P上运动时,猜想∠OQE的大小会发生怎样的变化?请对你的猜想加以证明.

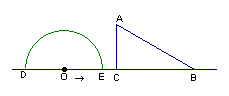
25.如图,形如量角器的半圆O的直径DE=12cm,形如三角板的⊿ABC中,∠ACB=90°,∠ABC=30°,BC=12cm。半圆O以2cm/s的速度从左向右运动,在运动过程中,点D、E始终在直线BC上。设运动时间为t (s),当t=0s时,半圆O在⊿ABC的左侧,OC=8cm。
(1) 当t为何值时,⊿ABC的一边所在直线与半圆O所在的圆相切?
(2) 当⊿ABC的一边所在直线与半圆O所在的圆相切时,如果半圆O与直线DE围成的区域与⊿ABC三边围成的区域有重叠部分,求重叠部分的面积。
 |
参考答案 选择题:C、B、B、B、D、D、D、C、B、C
二、填空题:11. 5(x+y); 12. 平行四边形、矩形、等腰梯形;
13. AB=DC 14、19; 15. ![]()
三、解答题:
16.(1)2; (2) x=2,y=1 (3)1≤x<3,整数解是1,2。
17.解:原式=![]() ·
·![]() =
=![]() =
=![]()
18.略
19.解:(1)设![]()
将(60,40),(70,30)代入得:
![]()
解得:![]()
![]() ……4分
……4分
(2)![]()
![]()
![]()
![]()
![]()

![]()
所以,当销售价是75元时,最大利润是625元,此时销量为25件。
www.czsx.com.cn
20.解:连结EC.
∵EF⊥BC,EG⊥CD,∴四边形EFCG为矩形.∴FG=CE.
又BD为正方形ABCD的对角线,∴∠ABE=∠CBE.
又BE=BE,AB=CB,∴△ABE≌△CBE.
∴AE=EC. ∴AE=FG.
21.(1)4分钟,40升 (2)y=-19x+325 , 2升
22、解:⑴24,24,25;
⑵对于线段AC与线段BD垂直相交(垂足O不与点A,C,B,D重合)的任意情形,四边形ABCD的面积为定值24。
证明如下:
∵AC⊥BD,
∴![]() ,
,![]()
∴![]()
![]()
⑶顺次连接点A,B,C,D,A所围成的封闭图形的面积仍为24
23.解:(1)100; (2分)
(2)30~39; (4分)
(3)0.16; (6分)
(4)12800. (8分)
24.解:(1)如图1,过C点作CD⊥x轴于点K,与⊙P相交于点D,
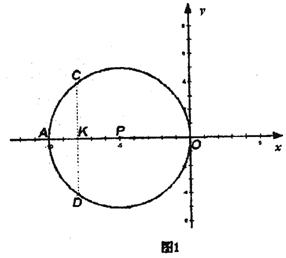
∵AO为直径.
∴CK=KD,![]()
∵点C的坐标为(-8,4),
∴CK=4,OK=8.
∴![]()
∴AK=2.
∴AO=10.
∴点A的坐标为(-10,0). …………………………2分
(2)∵P(-5,0),K(-8,0),
∴PK=3.
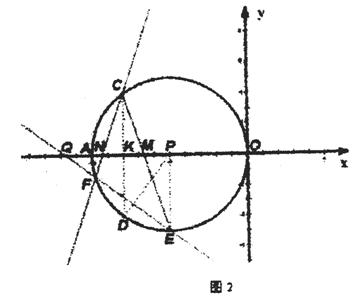
如图2,连结PD,PE,
∵m=-5,且P(-5,0),
∴PE⊥x轴于P.
又∵点E(-5,n)中⊙P上,且n<0,
∴点E的坐标为(-5,-5).
∵△CMN是以MN为底的等腰三角形,
∴∠CNM=∠CMN.
∴∠FCD=∠ECD.
∴![]()
∴PD⊥EF.
∴∠DPK=∠QEP.
∴Rt△KPD∽Rt△PEQ.
∴![]()
即![]()
∴![]()
∴![]()
∴点Q的坐标为![]()
设图象经过E、Q两点的一次函数的解析式为y=kx+b(k≠0),
∴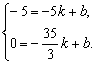
解得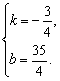
∴一次函数的解析式为![]()
(3)猜想:当点E在⊙P上运动时,∠OQE的大小始终保持不变.
证明:因为-10<m≤-5,n<0,可知点E(m,n)在⊙P的四分之一的圆上运动(点E不与点A、点D重合).
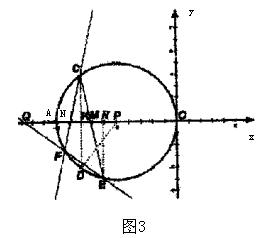
如图3,在⊙P的四分之一的圆上任取一点E(点E不与点A、点D重合),连结PD,过点E作EH⊥x轴于点H,
∵∠CNM=∠CMN,
∴∠FCD=∠ECD.
∴![]()
∴PD⊥EF.
∴∠OQE=∠PDK.
∵∠PDK的大小始终不变,
∴∠OQE的大小始终不变.
综上所述,当点E(m,n)在⊙P的四分之一的圆上运动(点E不与点A、点D重合)时,∠OQE的大小始终不变.
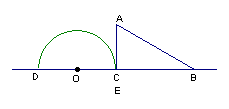 25.t=1s
t= 4s
25.t=1s
t= 4s
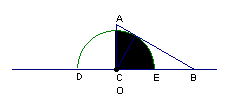 |
重叠部面积为9πcm2
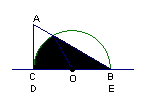
t=7s t=16s
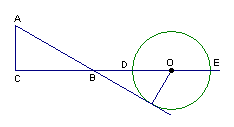
重叠部分面积为(9![]() +6π)cm2
+6π)cm2
