第一中学2005-2006年高中阶段学校招生考试模拟二（含答案）

数　学

　　　　考试时间为90分钟，满分为120分．

一、选择题（每小题3分，共15分．每小题给出的4个选项中只有一个是正确的，请

将所选选项的字母写在题目后面的括号内）

1．下列运算正确的是（　　）
（A）　 （B）－0.005＝5×
（C）　　（D）

2．如图1，某个反比例函数的图像经过点P．则它的解析式（　　 ）
（A）（x＞0）
（B） （x＞0）
（C）（x＜0
（D） （x＜0

3．下列说法中正确的是（　　 ）
（A）有两边和其中一边的对角对应相等的两个三角形全等
（B）等腰三角形是轴对称图形，也是中心对称图形
（C）对角线互相平分的四边形是平行四边形
（D）有两边平行的四边形是梯形

4．关于x的方程2（x－1）－a＝0的根是3，则a的值为（　　 ）
（A）4（B）－4　（C）5（D）－5

5．如图2，正方形的边长为a，以各边为直径在正方形内画半圆，所围成的图形（阴影部分）的面积为（　　）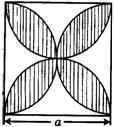
（A）　　　　 （B）2
（C）　　　 （D）

二、填空题（每小题4分，共20分．请把正确答实填写在横线上）

6．若∠A是锐角，cosA＝，则∠A＝　　　　　  。

7．不等式组的解集为　　　　　　　　  。

8．当a＋b＝3，x－y＝1时，代数式的值等于　　　　　 。

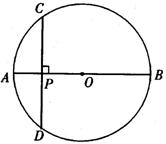
9．如图3，AB是⊙O的直径，弦CD⊥AB，垂足为P，若AP：PB＝1：4．CD＝8，则AB＝　　　　　　 。

10．与点 P（3，4）关于y轴对称的点的坐标为　　  ；
与点Q（－3，4）关于原点对称的点的坐标为　　  。

三、解答下列各题（每小题6分，共30分）

11．先化简后求值：，其中

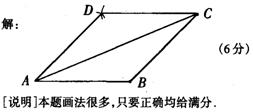
12．如图4，AB、AC分别是菱形ABCD的一条边和一条对角线，请用尺规把这个菱形补充完整．（保留作图痕迹，不要求写作法和证明）

13．如图5，灯塔A周围1000米水域内有礁石，一舰艇由西向东航行，在O处测得灯塔A在北偏东74°方向线上，这时O、A相距4200米，如果不改变航向，此舰艇是否有触礁的危险？（指定数学课使用科学计算器的地区的考生须使用计算器计算．以下数据供计算器未进入考场的地区的考生选用：cos74°＝0.2756，sin74°＝0.9613，cot74°＝0.2867，tan74°＝3.487）

14．在公式中，已知h、s、b．求a．

15. 某商场出售某种文具，每件可盈利2元，为了支援贫困山区，现在按原售价的7折出售给一山区学校，结果每件盈利0.2元（盈利＝售价－进货价）．问该文具每件的进货价是多少元？

四、（每小题7分，共28分）

16．已知二次函数的图像经过A（0，1），B（2，－1）两点．
（1）求b和c的值；
（2）试判断点P（－1，2）是否在此函数图像上？

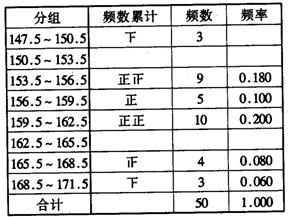
17. 为了了解中学生的身体发育情况，对某一中学同年龄的50名女学生的身高进行了测量，结果如下（单位：厘米）：


完成下面的频率分布表．

18．已知，为方程的两根，且+＝6，，求p和q的值．

19．如图6，在梯形ABCD中，AD∥BC，AD＝AB＝DC，BD⊥DC，求∠C的度数．

五、（每小题9分，共27分）

20．某人从A城出发，前往离A城30千米的B城．现在有三种车供他选择：①自行车，其速度为15千米/时；②三轮车，其速度为10千米/时；③摩托车，其速度为40千米/时．
（1）用哪些车能使他从A城到达B城的时间不超过2小时，请说明理由．
（2）设此人在行进途中离B城的路程为s千米，行进时间为小时，就（1）所选定的方案，试写出s与t的函数关系式（注明自变量t的取值范围），并在图7所给的平面直角坐标系中画出此函数的图像．

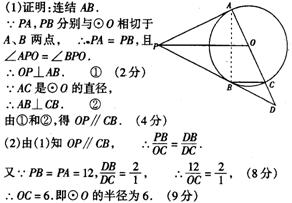
21. 如图8．PA和PB分别与⊙O相切于A，B两点，作直径AC，并延长交PB于点D．连结OP，CB．
（1）求证：OP∥CB；
（2）若PA＝12，DB：DC＝2：1，求⊙O的半径．

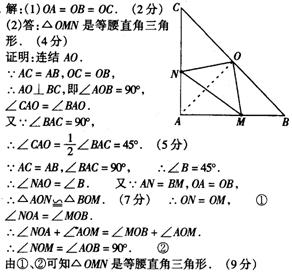
22．如图9．在Rt△ABC中，AB＝AC，∠BAC＝90°，O为BC的中点。（1）写出点O到△ABC的三个顶点 A、B、C（2）如果点M、N分别在线段AB、AC上移动，移动中保持AN＝BM，请判断△OMN的形状，并证明你的结论。

答案：

11.

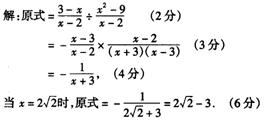
12.

13.

14.

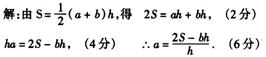
15.

16.

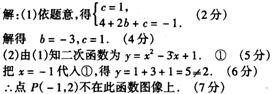
17.

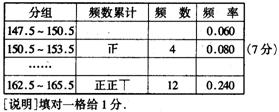
18.

19.

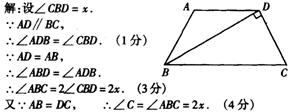
20.

21.

22.