2006年广东省初中数学竞赛初赛试卷
说明：考试时间：60分钟。总分120分。每小题4分。在每小题给出的四个选项中，只有
一项是符合题目要求的，并将答案填在下面的答题卡上。
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 答案 | |||||||||||||||
| 题号 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 答案 |
1.直角坐标平面上将二次函数y=－2（x－1）
－2的图象向左平移1个单位，再向上平移1个单位，则其顶点为（ ）。
A. （0，0） B. (1,－2) C. (0,－1) D.(－2,1)
2.下列的计算正确的是( ).
A.
(ab
)
=ab
B.(－3pq)=－6pq
C. x－
x＋
=( x－)
D.3(a)
－6a
=－3a
3.如图1.以直角三角形ABC三边为直径的半圆面积分别是
S
，S
，S
，直角三角形ABC面积是S，则它们之间的关系为（ ）.
 |
|
A. S= S＋S＋S
B. S= S＋S
C. S= S＋S C.
S= S
 |
图1
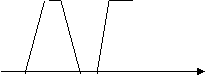
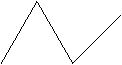
4. 一辆公共汽车从车站开出，加出速行驶一段时间后匀速行驶，过了一段时间，汽车到达下一个车站.乘客上下车后汽车开始加速，一段时间后又开始匀速行驶，下面可以近似地刻画出汽车在这段时间内的速度变化情况的是（ ）.
速度 速度
 | |||||
 |  | ||||
0 时间 0 时间
（A） （B）
 |
速度
速度
 | |||||
 | |||||
 | |||||
0 时间
0 时间
（D）
（C）
图2
5.如图3所示，在边长为a的正方形中挖去一个
边长为b的小正方形（a＞b），再把剩余的部分
剪拼成一个矩形，通过计算图形（阴影部分
的面积，验证了一个等式是（ ）. b b b
 |
A. a－b=（a+b）（a-b）
B. （a+b）= a+2ab+ b a a
C.
（a-b）= a-2ab+ b
图3
D.（a+2b）（a-b）= a+ab-2b
6.在一个仓库里堆积着正方体的货箱若干，要搬运这些箱子很困难,可是仓库管理员要落实一下箱子的数量,于是就想出一个办法:将这堆货物的三种视图画了出来,如图4.你能根据三视图,帮他清点一下箱子的数量吗?这些正方体箱的个数是( ).
A. 6 B. 7 C. 8 D. 9
主视图 左视图 俯视图
7.在Rt△ABC中,∠C=90°,则下列式子中不一定成立的是( ).
A.sinA=sinB B. cosA=cosB C.sinA=cosB D. sin(A+B)=sinC
8.体育课上全班女生进行了百米测验,达标成绩为18秒,下面是第一小组8名女生的成绩记录,其中正号表示成绩大于18秒,负号成表示绩小于18秒,则这组女生的达标率是( ).
| －1 | +0.8 | 0 | －1.2 | －0.1 | 0 | 0.5 | －0.6 |
A. B. C.
D. 
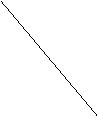
9.函数y=kx和y=
（k﹤0）在同一坐标系中的图象是（ ）.
y y
y y
 | |||||||
 | |||||||
 | |||||||
 | |||||||
0 x 0 0
x 0 x x
A
B
C D
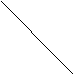
10.将一张正方形纸按图7所示的方式二次折叠,折叠后再按图所示沿MN裁剪,则可得( ).
A.多个等腰直角三角形
B. 一个等腰直角三角形和一个正方形
C. 四个相同的正方形
D. 两个相同的正方形
M
A
B A
B A B A
B
N N
D
C D
C D
C D
C
图7
11.某地2001年外贸收入为m亿元,若每年的增长率为1,则2003年外贸收入达到n亿元,则可以列出方程式( ).
A. m(1＋x)=n B.
(m＋x%)=n
C. m(1＋x)(1＋2x)=n D. m(1＋x%)=n
12.如图8.小正方形的边长均为1，则下列图中的三角形（阴影部分）与△ABC相似的是（ ）.
A
 |  |  |
A B C D B C
13.一件衣服标价132元,若以9折降价出售,仍可获利10%,则这件衣服的进价是( ).
A.106元 B.105元 C.118元 D.108元
14.若分式
的值为0,则x的值为( ).
A.2 B.±2 C.-2 D.±4
15.若x-2(k+1)x+4是完全平方式,则k的值为( ).
A.±1 B.±3 C.-1或3 D.1或-3
16.已知:如图9, △ABC中,P为AB上一点,在下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC=AP·AB;
④AB·CP=AP·CB,能满足△APC和△ACB相似的条件是( ). A
P
A .①②④
B.①③④
C.②③④
D.①②③
B C
17.已知在半径为2的⊙O中,内接三角形ABC的边AB=2
,则∠C的度数为( ).
A.60° B.30° C.60°或120° D.30°或150°
18.如果一直角三角形的三边长为a,b,c,∠B=90°,那么关于x的方程a(x-1)-2cx+b(x+1)=0的根情况是( ).
A.有两个相等的实数根 B. 有两个不相等的实数根 C.没有实数根 D. 无法确定
19.点P(9+
,-3+a),则点P所在象限为( ).
A.第一象限 B. 第二象限 C. 第三象限 D第四象限.
20.如果函数y=kx
的图象是双曲线,而且在第二、四象限,那么k=( ).
A.
B.-1
C.- 
D.1
21.若梯形上底的长为L,两腰中点连线的线段的长为m,那么连结两条对角线中点的线段长是( ).
A.m-2L B. 
-L
C.2m-L
D.m-L
22.菱形的一边和等腰直角三角形的直角边相等,若菱形的一角为60°,则菱形和等腰直角三角形的面积比是( ).
A.:2 B. :1
C.1: D. :4
23.若方程8x+2kx+k-1=0的两个实数根是x, x且满足x
+x
=1,则k的值为( ).
A.-2或6 B.-2 C.6 D.4
24. ⊙O的半径为10㎝,A是⊙O上一点,B是OA中点,点B和点C的距离等于5㎝,则点C和⊙O的位置关系是( ).
A.点C在⊙O内 B. 点C在⊙O上
C. 点C在⊙O外 D. 点C在⊙O上或⊙O内
25.⊙O和⊙O
相交于A,B两点,公共弦与连心线O O交于G,若AB=48, ⊙O和⊙O的半径分别是30和40,则△A O O的面积是（ ）.
A.600 B.300或168 C.168 D.600或168
26.在2004 2005 2006 2007 这四个数中,不能表示为两个整数平方差的数是( ).
A.2004 B.2005 C.2006 D.2007
27.如图10,BC是半圆O的直径,EF⊥BC于点F，
=5，又AB=8，AE=2，则AD的长为（ ）.A
D E
A.1+
B.
C. 
D. 1+
B F C
28.把△ABC沿AB边平移到△A
BC的位置，它们的重叠部分（即图11中阴影部分）的面积是△ABC的面积的一半，若AB=，则此三角形移动的距离A A是（ ）.
C C
A. -1
B.
C.1
D.
A A B B
29.若梯形ABCD的两条对角线与两底所围成的两个三角形的面积为P和q(如图12),则梯形的面积为( )
A.2(P+ q)
B.(p+q) C.
P+ q+pq D. P+ q+
D q C
P
A B
30.菱形的两条对角线之和为L,面积为S,则它的边长为( ).
A.
B. 
C. 
D.
答案如下:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 答案 | C | D | B | B | A | B | A | C | C | C | A | B | D | A | D |
| 题号 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 |
| 答案 | D | C | A | D | B | D | B | B | D | D | C | B | A | B | C |