九年级数学试卷

班级　　　 　 姓名　　　　　  　 座号　　　 得分　　　　　　

一.填空题(每小题3分,共30分,将正确答案填写在横线上)

1.如下图，修建抽水站时，沿着倾斜角为30⁰的斜坡铺设管道，若量得水管AB的长为80米，那么点B离水平面的高度BC的长为　　　　　　  米

2.某水坝迎水坡的坡度是，则它的坡角等于___________

3.在Rt⊿ABC中，∠C＝90°，BC＝10，AC＝4，则cosB=　　　 ,tanA=　　　　；

4抛物线，则其对称轴是　　　　　　 顶点坐标是　　　　　　 。

5.求与抛物线与x轴的交点坐标　　　　　　　　　　　　 。

6.初三(1)班共有48名团员要求参加青年志愿者活动，根据实际需要，团支部从中随机选择12名团员参加这次活动，该班团员李明能参加这次活动的概率是_______

7.等腰三角形的腰长为3，底边长为2，则底角的余弦值为　　　　  ；

8. 若∠A为锐角，且tanA是方程一个根，则∠A＝　　　　；

9. 抛物线y＝ax²＋3经过点（－1，5），则a＝　　　　 ．且当x　　　　　　　 时y随x的增大而增大。

10．如图，一居民生活小区内有一块三角形空地，为了美化环境，决定在这块空地种植花草，预计每平方米投入绿化资金20元，

那么共需要资金　　　　　　　　　　 元。

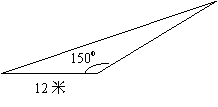　　　　　　 　　　　　　　　　　　　　　　　　第10题

　　　　　　　　　　　　　　　　　　　　

二．选择题(每小题3分,共30分,将正确答案的选项填在以下括号内中)

11. 在△ABC中，A，B为锐角，且有 ，则这个三角形是（　　）　　　

A. 等腰三角形　B.直角三角形　C.钝角三角形　D. 锐角三角形

12.sin60°、cos60°、tan60°的大小关系是（　　）　　　　　　　　　　　　　　　　　

A.sin60°>cos60°>tan60°　　　　 B. tan60°>cos60°>sin60°

C. cos60°> sin60º> tan60°　　　　D. tan60º > sin60º >cos60º

13.对角线互相垂直平分且相等的四边形一定是（　　  ）

　　A.正方形　　　B.菱形　　  C.矩形　　　D.等腰梯形

14.对于的图象下列叙述正确的是　（　　）

A .a的值越大，开口越大　　　　　 B .a的值越小，开口越小

C.a的绝对值越小，开口越大　　　　D.a的绝对值越小，开口越小

15.直角坐标平面上将二次函数y＝-2(x－1)²－2的图象向左平移１个单位，再向上平移１个单位，则其顶点为（　　）

A.(0，0)　　　 B.(1，－2)　　　　 C.(0，－1) 　　　　　D.(－2，1)

16.函数的图象与轴(　　)

A．有一个交点　　　B．有两个交点　　　C．有交点　　　 D．没有交点

17.已知△ABC中，AD是高，AD=2，DB=2，CD=2，则∠BAC=（　　）

　 A. 105⁰　 　　B. 15⁰　　　　 C.105⁰或15⁰　　 D. 60⁰

18. 当锐角时，的值为（　　）　　　　　　　  　　　　　　　　　　 

A　　小于　　　 B　 大于　　  C　　小于　  D　　大于

19． “圆柱与球的组合体”如下左图所示，则它的三视图是（　　　 ）

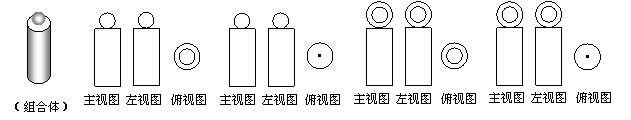
　　　　　　  A　　　　　　　  B　　　　　　　  C　　　　　　　 D

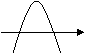
20．已知：a＜0,b＞0; 那么+3的图象大致为 (　  )

y　　　　　　　  y　　　　　　　　　  y　　　　　　  y

O　　　x　　　  O　　　　 x　　  O　　 x　　　　 O　　　x

　　　　  A　　　　　　　　 B　　　　　　  C　　　　　　 D

三．计算题(每小题5分,共10分)

21．计算：　　22．用配方法将二次函数

　　　　　　　　　　　　　　　　　　　 写成的形式

四．解答题(8小题,共80分,写出必要的步骤,直接写出答案不得分)

23. (9分) 在⊿ABC中，已知∠B = ，∠C =，，求、与∠A；

24. (9分)某企业的年产值在两年内从1000万元增加到1210万元，求平均每年增长的百分率。

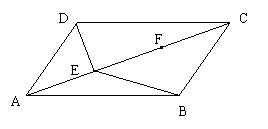
25．（10分）如图，在ABCD中，点E、F在对角线AC上，且AE＝CF．请你以F为一个端点，和图中已标明字母的某一点连成一条新线段，猜想并证明它和图中已有的某一条线段相等（只需证明一组线段相等即可）．

⑴ 连结______________．

⑵ 猜想：____________ ＝ ____________．

⑶ 证明：

26． (10分)有一种螃蟹，从海上捕获后不放养，最多只能存活两天.如果放养在塘内，可以延长存活时间，但每天也有一定数量的蟹死去.假设放养期内蟹的个体质量基本保持不变，现有一经销商，按市场价收购这种活蟹1000 kg放养在塘内，此时市场价为每千克30元，据测算，此后每千克活蟹的市场价每天可上升1元，但是，放养一天需支出各种费用为400元，且平均每天还有10 kg蟹死去，假定死蟹均于当天全部销售出，售价都是每千克20元.

(1)设x天后每千克活蟹的市场价为p元，写出p关于x的函数关系式;

(2)如果放养x天后将活蟹一次性出售，并记1000 kg蟹的销售总额为Q元，写出Q关于x的函数关系式.

(3)该经销商将这批蟹放养多少天后出售，可获最大利润(利润=Q－收购总额)？

27．(10分)求二次函数的图象与x轴的交点坐标，并作草图验证。

28．(10分)在某高速公路建设中，要沿AC方向开山修路，为加快施工进度，要在山坡　 的另一边同时施工.如图12所示，从AC上的一点B量取∠ABD=150°，BD=420 m，　　　　∠D=60°，那么开挖点E离D多远正好使A、C、E成一直线?

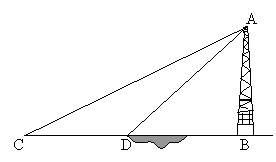29．(10分)如图，河对岸有铁塔AB，在C处测得塔顶A的仰角为30°，向塔前进14米到达D，在D处测得A的仰角为45°，求铁塔AB的高。

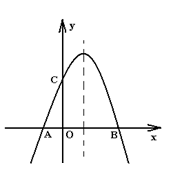
30. (12分)如图，抛物线与x轴分别交于A、B两点，与轴交于C点.点A、B、C的坐标分别是(－1,0);(3, 0);(0, 2)

(1) 求此抛物线对应的函数解析式；

(2) 若点P是抛物线上位于x轴上方的一个动点，求△PAB面积的最大值.

　 (3)当x取何值时，y＞0.