九年级数学期中试卷
(全卷满分为150分，考试时间为120分钟)
一． 选择题 （每小题4分，十小题共40分）
1. 绝对值为4的实数是（ ）
A. ±4 B. 4
C. －4 D. 2
2. 把二次函数
配方成顶点式为（ ）
A． 
B． 
C． 
D．
3. 如图，A、B、C三点在⊙O上，且
，则
等于( )
A. 
B.
C. 
D. 
4.已知小明同学身高1.5米，经太阳光照射，在地面的影长为2米，若此时测得一塔在同一地面的影长为60米，则塔高应为（ ）
A. 90米 B. 80米 C. 45米 D. 40米
5. 下列多边形中，既是轴对称图形又是中心对称图形的是（ ）
A. 平行四边形 B. 正方形 C. 等腰梯形 D. 等边三角形
6. 若"！"是一种数学运算符号，并且1！=1，2！=2×1=2，3！=3×2×1=6，4！=4×3×2×1，…，则 的值为（ ）
A. B. 99! C. 9900 D. 2！
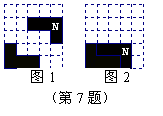7.在5×5方格纸中将图（1）中的图形N平移后的位置如图（2）中所示，那么正确的平移方法是（ ）.
(A)先向下移动1格，再向左移动1格
(B)先向下移动1格，再向左移动2格
(C)先向下移动2格，再向左移动1格
(D)先向下移动2格，再向左移动2格
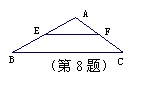8. 如图所示，BC＝6，E、F分别是线段AB和线段AC的中点，
那么线段EF的长是（ ）．
（A）6 （B）5 （C）4.5 （D）3
9. 下列命题中，正确的是（ ）
A. 同位角相等 B. 平行四边形的对角线互相垂直平分
C. 等腰梯形的对角线互相垂直 D. 矩形的对角线互相平分且相等
10. 函数
自变量x的取值范围是( )
A.x≤-2
B.x≥-2 C.x≥2 D.x≤2
二． 填空题（每小题4分，五小题共20分）
11. 如果收入15元记作＋15元，那么支出20元记作 元
12. 抛物线ｙ＝(ｘ－1)2+２的对称轴是_______，顶点坐标是_____
13. 已知△ABC∽△A′B′C′，且
，△ABC的面积为2㎝2，
则△A′B′C′的面积为 ㎝2.
14. 台湾是我国最大的岛屿，总面积为35 989.76平方千米，这个数据用科学记数法表示为 平方千米(保留两个有效数字)．
15. 用" 
"、"
"定义新运算：对于任意实数a，b，都有a b=a和a b=b，例如3 2=3，3 2=2。则(2002 2000) (2004 2003)=___________
三．解答题(第小题8分，选做四小题并在题号前打钩，共32分)
16.解方程
17.计算：
.
 |
18.已知：如图，AB＝AC,AE＝AD，点D、E分别在AB、AC上．
求证：∠B＝∠C．
19已知不等式：⑴1－x＜0；⑵
＜1；⑶ 2x+3＞1；⑷ 0.2x－3＜－2．你喜欢其中哪两个不等式，请把它们选出来组成一个不等式组，求出它的解集，并在数轴上把解集表示出来．
20.甲、乙两人玩“石头、剪刀、布”的游戏，试求在一次比赛时两人做同种手势（石头、石头）的概率（要求用树状图或列表法求解）
四．(每小题10分，选做两小题并在题号前打钩，共20分)
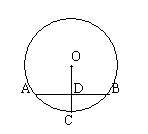
21. AB是⊙O的弦，半径 
于点D，且AB=8cm，
，
求OD的长。
22. 已知二次函数ｙ＝ｘ２－２ｘ－３
（１） 画出这个函数的图象。
（２） 支出它的对称轴、顶点坐标。
（３） ｘ取何值时，ｙ有最小值，最小值是多少？
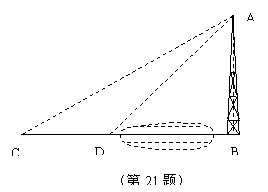23. 如图，河对岸有一铁塔AB。在C处测得塔顶A的仰角为30°，
向塔前进16米到达D，在D处测得A的仰角为45°，求铁塔AB的高。(结果保留根号)
五．(每小题12分，选两小题做，共24分)
24. 在正常情况下，一个人在运动时所能承受的每分钟心跳的最高次数S（次/分）是这个人年龄n（岁）的一次函数。
（1）根据以上信息，求在正常情况下，S关于n的函数关系式；
（2）若一位63岁的人在跑步，医生在途中给他测得10秒心跳为26次，问：他是否有危险？为什么？
25. 如图，用长为18 m的篱笆（虚线部分），两面靠墙围成矩形的苗圃.
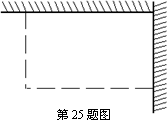（1）设矩形的一边为
（m），面积为
(m2)，求关
于的函数关系式，并写出自变量的取值范围；
（2）当为何值时，所围苗圃的面积最大，最大面积是多少？
26. 某商店购进一批单价为20元的日用商品，如果以单价30元销售，那么半月内可以售出400件，根据销售经验，提高销售单价会导致销售量的减少，即销售单价每提高1元，销售量相应减少20件，如何提高售价，才能在半月里获得最大利润？并求出最大利润。
六．本题14分(选一小题做，共14分)
27、班委会决定，由小敏、小聪两人负责选购圆珠笔、钢笔共22支，送给结对的山区学校的同学，他们去了商场，看到圆珠笔每支5元，钢笔每支6元。
(1)、若他们购买圆珠笔、钢笔刚好用去120元，问圆珠笔、钢笔各买了多少支？
(2)、若购圆珠笔可9折优惠，钢笔可8折优惠，在所需费用不超过100元的前提下，请你写出一种选购方案。
28．如图：一位篮球运动员跳起投篮，球沿抛物线
运行，然后准确落入篮筐内，已知篮筐的中心离地面的距离为３.05米，
（１）球在空中运行的最大高度为多少米？
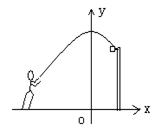（２）如果该运动员跳投时球出手离地面的高度为2.25米，请问他距离篮筐中心的水平距离是多少米？
29.如图，在一块三角形区域ABC中，∠C=90°，边AC=8，BC=6，现要在△ABC内建造一个矩形水池DEFG，如图的设计方案是使DE在AB上。
⑴求△ABC中AB边上的高h;
⑵设DG=x,当x取何值时，水池DEFG的面积最大？
⑶实际施工时，发现在AB上距B点1.85的M处有一棵大树，问：这棵大树是否位于最大矩形水池的边上？如果在，为保护大树，请设计出另外的方案，使三角形区域中欲建的最大矩形水池能避开大树。