九年级提前批数学模拟试题
一．填空题（每空5分，共40分，其中1—8任选7题，9、10任选1题，多做不加分）
1.一元二次方程
有根的k的取值范围是________________;
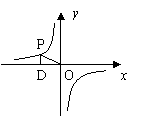
2.如图，点P是反比例函
数
上的一点，PD⊥
轴于点D，则△POD的面积为
;
3. 如果甲邀请乙玩一个同时抛掷两枚硬币的游戏，游戏的规则如下：由乙抛掷，同时
出现两个正面，乙得1分；抛出一正一反，甲得1分. 谁先累积到10分，谁就获胜.你认
为 （填“甲”或“乙”）获胜的可能性更大
4．AB、AC与⊙O相切于B、C，∠A=50O，点P是圆上异于B、C的一动点，∠BPC的度数是 ；
5.如图，已知
∠B＝20°，则∠
＝_____;
(2题图) (5题图) (6题图) (8题图)
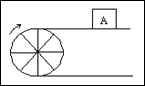6.如图，当半径为30cm的转动轮转过1200角时，传送带上的物体A平移的距离为
cm。
7.如图，在一个房间内，有一个梯子斜靠在墙上，此时梯子的倾斜角为75°. 梯子顶端距地面的垂直距离MA为5米，如果梯子底端不动，顶端靠在对面墙上，此时梯子的倾斜角为45°.则这间房子的宽AB是________米；
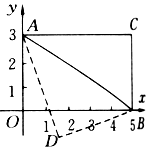
8.如图，矩形AOBC，以O为坐标原点，OB，OA分别在x轴，y轴上，点A坐标为（0,3），∠OAB＝60°,以AB为轴对折后，使C点落在D点处，则D点的坐标 .
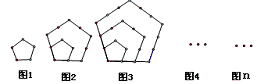9.右图由正五边形构成，在图1中有5个点，图2中有12个点，图3 中有22个点，以此类推，图4(最长边上有5个点)中共有 个点；
图n（最长边上有n＋1个点）中共有
_________个点。（用含n的代数式表示）。
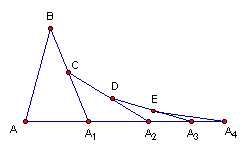
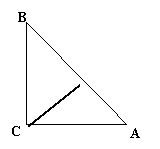
10．如图，作等边△ABC，取AC的中点D，以AD为边
向△ABC形外作等边△ADE，取AE的中点G，再以EG
为边作等边△EFG，如此反复，当作出第6个三角形时，
若AB=4，整个图形的外围周长是 .
二、选择题（每题6分，共72分）
11．设a、b、c、d、e的值均为0、1、2中之一，且a+b+c+d+e=6，a2+b2+c2+d2+e2=10，则a3+b3+c3+d3+e3的值为 （ ）
（A）14 （B）16 （C）18 （D）20
12.下列说法正确的有（ ）个
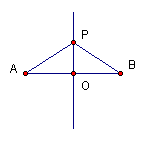
（1） 如下图，已知PA＝PB，则PO是线段AB的垂直平分线；
（2） 对于反比例函数
，（x1,y1）,（x2,y2）是其图象上两点，若x1<x2,则y1>y2；
（3） 对角线互相垂直平分的四边形是菱形；
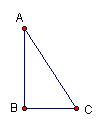
（4） 如下图，在△ABC中，∠A＝30°BC=2，则AC＝4;
（5） 一组对边平行的四边形是梯形；
（6）
是反比例函数；
（7）若一个等腰三角形的两边长为2和3,那么它的周长为7.
（12题图） (13题图)
A.0 B.1 C.2 D.5
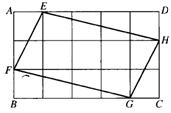
13．如图，将矩形ABCD分成15个大小相等的正方形，E、F、G、H分别在AD、AB、BC、CD边上，且是某个小正方形的顶点.若四边形EFGH的面积为1,则矩形ABCD的面积是（ ）
A.2
B.
C.
D.
14．若关于x的不等式组
有解，则函数y=（a-3）x2-x-
图象与x轴的交点个数为（ ）
（A）0 （B）1 （C）2 （D）1或2
15．龟兔赛跑，它们从同一地点同时出发，不久兔子就把乌龟甩在后面，于是兔子便得意洋洋地躺在一棵大树下睡觉。乌龟一直坚持不懈、持之以恒地向终点跑着，兔子一觉醒来，看见乌龟快接近终点了，这才慌忙追赶，但最终输给了乌龟.下列图象中能大致反映龟兔行走的路程S随时间t变化情况的是： （ ）
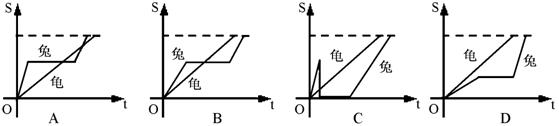
16．若
是二次函数
的图象上的两点,且
，则当
时，
的值为…………………………………………………（ ）
（A）0 （B）
（C）
（D）
17．如图，A是半径为1的⊙O外的一点，
是⊙O的切线，B是切点，弦
，连接
，则阴影部分的面积等于……………………（
）
A、
B、
C、
D、
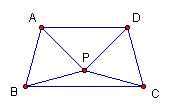
18．如图，△ABP与△CDP是两个全等的等边三角形，且PA⊥PD.有下列四个结论：①∠PBC＝15°;②AD∥BC；③直线PC与AB垂直；④四边形ABCD是轴对称图形.其中正确的结论的个数为（ ）
A.1
B.2
C.3
D.4
(18题图) (19题图) (21题图)
19．如图，已知⊙O的半径是R，C、D是直径AB同侧圆周上的两点，弧AC的度数为960，弧BD的度数为360，动点P在AB上，则PC+PD的最小值为………………………（ ）
A、2R B、
C、
D、R
20．正五边形对角线长为2，则边长a为（ ）
（A）
-1
（B）+1 （C）3- （D）2-3
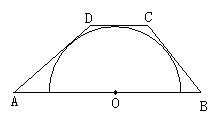
21．如图，圆O的圆心在梯形ABCD的底边AB上，并与其它三边均相切，若AB=10，AD=6，则CB长（ ）
（A）4 （B）5
（C）6 （D）无法确定
22．平面直角坐标系中，已知点P0（1，0），将点P0绕原点O按逆时针方向旋转30°得到P1，延长OP1到P2，使OP2=2OP1；再将P2绕点O按逆时针方向旋转30°得P3，然后延长OP3到P4，使OP4=2OP3；……；如此下去，则点P2004的坐标为（ ）
（A）（-22004，0） （B）（-21002，0） （C）（0，21002） （D）（21002，0）
三、解答题 （共38分）
23、（12分）某公司2005年1－3月的月利润y（万元）与月份x（月）之间的关系如图所示．图中的折线可近似看作是抛物线的一部分．(1)求出月利润y（万元）与月份x（月）之间的函数关系式
（2）公司开展技术革新活动，定下目标：今年6月份的月利润仍以图中抛物线的上升趋势上升．预计6月份公司的利润将达到多少万元？
（3）如果公司1月份的利润率为13%，以后逐月增加1个百分点．已知6月上旬平均每日实际销售收入为3.6万元，照此推算，6月份公司的利润是否会达到或超过（2）中所确定的目标？
（成本总价＝利润÷利润率，销售收入＝成本总价＋利润）
 |
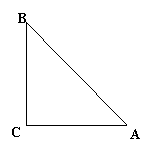24、（12分）定义：若某图形可分割为若干个都与它自己相似的图形，则称这个图形是自相似图形． 探究：
（1）如图甲，已知△ABC中，∠C＝90°，你能
把△ABC分割成2个都与它自己相似的小直角三角形
吗？若能，请在图甲中画出分割线，并说明理由．
答：
|
（2）一般地，“任意三角形都是自相似图形．”只要顺次连结三角形各边中点，则可将原三角形分割为4个都与它自己相似的小三角形．我们把△DEF（图乙）第1次顺次连结各边中点所进行的分割，称为1阶分割（如图1）；把1阶分割得出的4个小三角形再分别顺次连结它们各边中点所进行的分割，称为2阶分割（如图2）；…；依此规则操作下去．
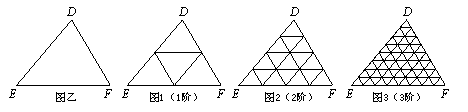
n阶分割后所得的小三角形均互相全等（n为正整数），设此时小三角形的面积为S1．
① 若△DEF的面积为10000，当n为何值时，2＜S1＜3？ （请你进行尝试估算!）
②当n＞1时，△DEF的面积记为S,请写出一个反映S、S1和n之间关系的等式．（不必证明）
25. （第1题，每空1分，共2分；第2题4分；第3题4分；第4题，每题2分，共4分；此题共14分）
探索一个问题：“任意给定一个矩形A，是否存在另一个矩形B，它的周长和面积分别是已知矩形周长和面积的一半？”（完成下列空格）
（1） 当已知矩形A的边长分别为6和1时，小明是这样研究的：设所求矩形的两边分别是
，由题意得方程组：
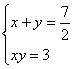，消去y化简得：
∵△＝49－48>0 ∴
∴满足要求的矩形B存在.
（2） 如果已知矩形A的边长分别为2和1，请你仿照小明的方法研究是否存在满足要求的矩形B.
（3） 如果矩形A的边长为m和n，请你研究满足什么条件时，矩形B存在？
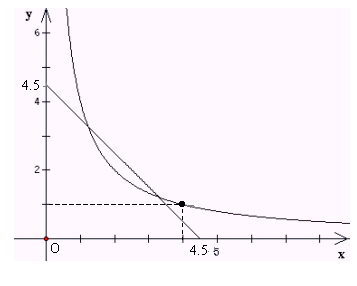
（4） 如图，在同一平面直角坐标系中画出了一次函数和反比例函数的部分图象，其中x和y分别表示矩形B的两边长，请你结合刚才的研究，回答下列问题：
a) 这个图象所研究的矩形A的两边长为_____和_____;
b) 满足条件的矩形B的两边长为_____和_____.
 |
参考答案：
一、填空题 1.
； 2.1； 3.甲； 4.65°或115°； 5.10°； 6.20∏；
7.5米； 8.(
-)； 9.35,
2+
； 10.
二、选择题 C B B D B B B D B A A B
三、解答题
23、解：(1)由题意可得A(1,3) B(2,4) C(3,6)
所以设解析式为：y=ax2+bx+c
代入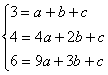得：
解得：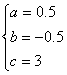
所以解析式为：y=0.5x2-0.5x+3 (1≤x≤3)
(2)当x=6时,y=0.5×36-0.5×6+3=18（万元）
c) 由题意得：3.6×30=108
+18=118 
不能达到（2）中的目标
24、（1）如图过C作AB的垂线（理由略）
（2）由题可得S=22n ·S1 22n ·S1=10000
2＜S1＜3 n=6
(3) S=22n ·S1
25、（1），2 ； （2） 设所求矩形的两边分别是，由题意得方程组：
，消去y化简得： 
∵△＝9－16＜0 ∴满足要求的矩形B不存在.
（3）设所求矩形的两边分别是，由题意得方程组：
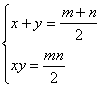，以
为根的方程为
满足要求的矩形B若存在，△＝
≥0.
∴
(或
)
(4) a) 1 ,8 ； b) 
,