陆河县上护中学九年级数学竞赛试题

班级______　座号_______　姓名______　成绩_______

一、填空题(每小题3分，满分36分)

1.我省耕地面积居全国之首，达13 300多万亩，用科学记数法表示13 300为____________。

2.，，且>0，则-的值等于_________________。

3.如果一次函数的图象与轴交点到原点的距离为4，那么的值为_____________。

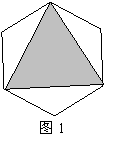
4.已知：如图1，正六边形ABCDEF的边长为2，则图中阴影部分的面积为_____。

5.已知△ABC是等边三角形，AB=6，点O到BC的距离为2，且OB=OC，则O、A 两点的距离是_____________。

6.在学校举行的运动会上，小勇和小强都进入了200米决赛，小勇用了秒，小强用了秒，小强获得了200米决赛的冠军，则小强比小勇平均每秒多跑_____________米。

7.若等腰三角形的两个内角之和为140⁰，则顶角的度数为__________。

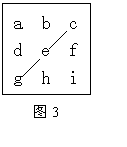
8.图2为2005年3月日历。图3是用一长方形的方框在日历中框出9天的日期，若从左下角到右上角“对角线上”三个数的和为69，则这9天中，最后一天是________号。

9.某商品经过两次降价，由原价100元下调至81元，则平均每次降价的百分率是____________。

10.若点P(，-5)与Q(1，)关于原点对称，则的值为_______。

11.如图4，凸四边形ABCD的四边AB、BC、CD和DA的长分别是3、4、12和13，∠ABC=90⁰，则四边形ABCD的面积S____________。

12.将一根细长的绳子，沿中间对折，再沿对折后的绳子中间对折，这样连续沿中间对折5次，用剪刀沿对折5次后绳子的中间将绳子全部剪断，此时绳子被剪成_____________段。

二、选择题(每小题3分，满分24分)

13.若不论取何值时，分式总有意义，则的取值范围是(　　 )

A.　　  B. 　　　 C. 　　　D.

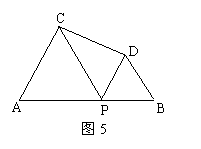
14.如图5，已知AB=20，P是线段AB上任意一点，在AB的同侧分别以AP和PB为边作等边△ACP和等边△BPD，则线段CD长度的最小值是(　　 )

A.8　　　 B.10　　　　C.12　　　 D.

15.在平坦的草地上有A、B、C三个小球，且A、B、C在一条直线上，若A球和B球相距3米，A球和C球相距1米，则B球与C球相距是(　　  )

A.4米　　　 B.2米　　　 C.4米或2米　　　 D.1米或2米

16.已知在正比倒函数的图象上两点，，当<，有>，那么的取值范围是(　　 )

A.　　　 B.　　  C.　　  D.

17.张师傅下岗再就业，做起了某种小商品生意。进货时，以每件元的价格购进甲种小商品20件，每件元的价格购进乙种小商品24件(>)；回来后，根据市场行情，他将这两种小商品都以每件元的价格售出，全部

售出后张师傅赚得的钱数为(　　)

A.元　　B. 元　　C. 元　　 D. 元

18.已知抛物线的系数满足，则这条抛物线一定经过点(　　 )

A.（0,2）　  B.（2，0）　　 C. （0,-2）　 　D. （-2，0）

19.若实数，满足且，则的值是(　　　)

A.　　　　B.　　　　C.-2005　 　　D.2005

20.已知三角形三个内角的度数都是质数，则这三个内角中必定有一个内角等于（　　　）

A.2⁰　　　　B.3⁰　　　　C.5⁰ 　D.7⁰

三、解答题（满分60分）

21.（本题5分）

已知：关于的一元二次方程有两个不相等的实数根。

（1）求的取值范围；

（2）当方程两根之积的倒数等于两根之和的4倍时，求的值。

22.图6表示甲、乙两名选手在一次自行车越野赛中，各时间段的平均速度

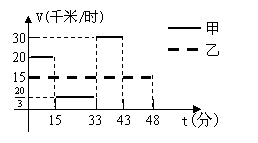v（千米/时）随时间t（分）变化的图象（全程），根据图象提供的信息：

（1）求这次比赛全程是多少千米？

（2）求比赛开始后多少分钟两人相遇？

23.在△ABC中，AB＝25cm，BC＝15cm,CA=20cm，以C为顶点作一个等边三角形，其它两个顶点在△ABC的边上，求这个等边三角形的高。

24.某学校图书馆准备向某一出版社邮购（是10的整数倍）本课外读物，每本书的单价为15元，出版社规定：邮购10本以下（包括10本）需加邮费6元；邮购10本以上（不包括10本）需加的邮费为书价的10%。在邮局汇款时，每100元汇款需付汇费1元，汇款额不足100元时，按100元汇款收取汇费。

（1）如果图书馆每次邮购10本，分次邮购，　那么所需的费用为790元。求的值。

（2）在（1）问的情况下，求一次性邮购本课外读物的费用；

（3）如果邮购60本课外读物，试比较分6次邮购和一次邮购这两种方式中，哪种邮购方式费用小？

25.在平面直角坐标系中，直线与轴交于点A（32，0），与轴交于

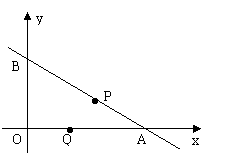点B（0，24），动点P以每秒4个单位长度的速度从A点出发，在线段AB上向B点匀速运动；动点Q以每秒5个单位长度的速度从O点出发，在线段OA上向A点匀速运动。P、Q两点同时出发，当Q点到达A点时，两点同时结束运动。设动点P、Q的运动时间为t秒。

（1）求、的值；

（2）当t＝3.2时，判断△APQ的形状。

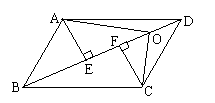26.（本题8分）

已知：在　ABCD中，O是对角线BD上任意一点，

易证：

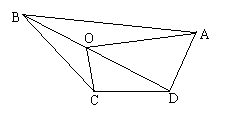（1）在一般四边形中，能否得出与上面相类似的结论，如果能，请结合所给图形写出结论并给予证明；如果不能，请说明理由。

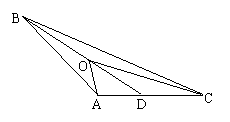（2）在三角形中，你又能否得出与上面相类似的结论，如果能，请结合所给图形写出结论并给予证明；如果不能，请说明理由。

27.（本题10分）

为了进一步提高企业效益，某企业决定引入一条新的生产线，为此要将企业原有的100名职工派出一部分到新生产线工作。分工后，继续在原生产线从事生产的职工人均年产值可增加20%，而分派到新生产线工作的职工人均年产值为分配前人均年产值的4倍。如果分工后，原生产线的年总产值不少于分工前原生产线的年总产值；而新生产线的年总产值不少于分工前原生产线的年总产值的一半。

（1）确定到新生产线的职工分派方案；

（2）引入新的生产线后要使企业年总产值最大，球分派到新生产线的职工人数。

得分 0 5 10 15 20 25 …… 90 95 100 人数 0 0 1 6 5 4 …… 7 2 1

28.某校举办“实践杯”知识竞赛，本次比赛共20道选择题，每道题5分，得分与人数的统计如下表：

其中得分下低于25分的选手的平均分为80分；得分不高于90分的选手的平均分为70分。求此次参赛选手的人数。