华东师大版九年级第二学期期末测试卷班级　 姓名　　成绩 　　

(100分  90分钟)

一、选择题:(每题2分,共26分)

　1.函数y=的自变量x的取值范围是(　 )

　　A.　　 B.;　　　　C.;　　 D.

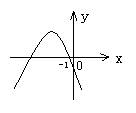  2.抛物线y=x²-6x+24的顶点坐标是(　 )

　　A.(-6,-6)　　　B.(-6,6);　　　　C.(6,6)　　　  D.(6,-6)

　3.过(-1,0),(3,0),(1,2)三点的抛物线的顶点坐标是(　 )

　　A.(1,2)　　　B.(1,);　　　 C.(-1,5)　　 D.(2,)

　4.如图所示,函数y=ax²-bx+c(a≠0)的图象过点(-1,0),则的值是(　 )　　　　 A.-3　　　　B.3　　　　　 C.　　　　D.-

　5.已知一次函数y=ax+c与二次函数y=ax²+bx+c(a≠0), 它们在同一坐标系内的大致图象是图中的(　 )

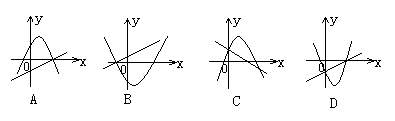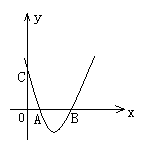
　6.如图所示,二次函数y=x²-4x+3的图象交x轴于A、B两点, 交y 轴于点C, 则△ABC的面积为(　 )　　　　  A.6　　 B.4　　  C.3　　D.1

　　　　　　　　　　　 

　　　　(第6题)　　　　　　　 (第7题)　　　(第9题)　　　 (第11题)

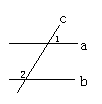
　7.如图所示,a∥b,若∠1=50°,则∠2的度数为(　 )

　　A.50°　　B.120°　　 C.130°　　 D.140°

　8.等腰三角形一边长等于5,一边长等于9,则它的周长是(　 )

　　A.19　　　B.23　　 C.19或23　  D.14

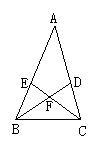
　9.如图所示,在△ABC中,AB=AC,∠A=36°,BD、CE分别为∠ABC与∠ACB的角平分线,且相交于点F,则图中的等腰三角形有(　 )

　　A.6个　  B.7个　　 C.8个　  D.9个

　10.平行四边形ABCD的对角线的交点在坐标原点,且AD平行于x轴,若A点坐标为(-1,2),则C点的坐标为(　 )

　　A.(1,-2)　　 B.(2,-1);　　　C.(1,-3)　　 D.(2,-3)

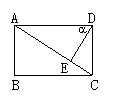
  11.如图所示,在矩形ABCD中,DE⊥AC于E,设∠ADE=α,且cosα=,AB=4,则AD 的长为(　 )　　　A.3　　　　 B.　　C.　　　 D.

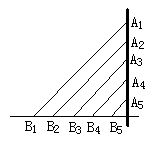
　12.斜拉桥是利用一组组钢索,把桥面重力传递到耸立在两侧的高塔上的桥梁, 它不需建造桥墩.如图所示A₁B₁、A₂B₂、…、A₅B₅是斜拉桥上5条互相平行的钢索, 并且B₁、B₂、B₃、B₄、B₅被均匀地固定在桥上.如果最长的钢索A₁B₁=80m,　最短的钢索A₅B₅=20m,那么钢索A₃B₃、A₂B₂的长分别为(　 )

A.50m、65m; B.50m、35m;　C.50m、57.5m;　D.40m、42.5m

　13.某校初三(一)班一组女生体重数据统计表如下:

体重(千克)	40	42	44	46	51
人数(人)	1	0	3	2	1

　　该组女生体重的平均数、众数、中位数分别是(　 )

　　A.45、44、44　　　B.45、3、2;　　 C.45、3、44　　　 D.45、44、46

二、填空题:(每题2分,共26分)

　14.函数y=的自变量x的取值范围是________________.

　15.抛物线y=x²-2x+3的顶点坐标为___________.

16.若二次函数y=x²+bx+c的图象经过点(-4,0)、(2,6),  则这个二次函数的关系式为__________________.

　17.已知点(1,3)是双曲线y=与抛物线y=x²+(k+1)x+m的交点,则k 的值等于______.

　18.已知二次函数y=-4x²-2mx+m²与反比例函数y=的图象在第二象限内的一个交点的横坐标是-2,则m的值是_______.

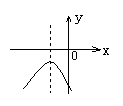
　19.二次函数y=ax²+bx+c的图象如图所示,则ac_____0(填“>”、“<”、“＝)”

　20.如图所示,AB∥CD,直线EF分别交AB、CD于点E、F,EG平分∠BEF,若∠1=72°,则∠2=_______.

　21.等腰三角形一腰上的高与另一腰的夹角为30°,腰长为a,则其底边上的高是_________.

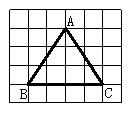
　22.在方格纸上有一个△ABC,它的顶点位置如图所示,则这个三角形是______三角形.

　　　　　　　　　　　　　　　　　　

　　　 (第19题)　　　　　　　  (第20题)　　　　(第22题)　　　　　  (第25题)

　23.用长为100cm的铁丝制成一个矩形,其面积为625cm²,那么这个矩形的对角线长为_______cm(结果有根号的保留根号)

　24.已知菱形较大角是较小角的3倍,并且高为4cm, 那么这个菱形的面积是_______.

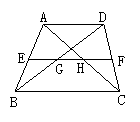
　25.如图所示梯形ABCD中,AD∥BC,中位线EF分别与BD、AC交于点G、H,若AD=6, BC=10,则GH=________.

　26.某公园在取消售票之后对游园人数进行10天统计,结果有3天是每天800人游园,有2天是1200人游园,有5天是600人游园,则这10 天平均每天游园的人数是_____

三、解答题:(每题7分,共42分)

　27.已知函数y=x²+bx+c过点A(2,2),B(5,2).

(1)求b、c的值;(2)求这个函数的图象与x轴的交点C的坐标; (3)求的值.

　28.已知二次函数y=ax²+bx+c(a≠0)的图象经过一次函数y=-x+3的图象与x 轴、y轴的交点,并且经过点(1,1),求这个二次函数的关系式.

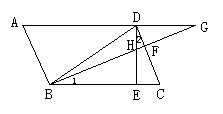
　29.如图,ABCD中,∠DBC=45°,DE⊥BC于点E,BF⊥CD于点F,DE、BF相交于点H, BF、AD的延长线相交于G.求证:(1)AB=BH;(2)AB²=GA·HE.

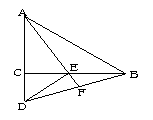
　30.如图,△ACB、△ECD都是等腰直角三角形,且C在AD上,AE的延长线与BD 交于F,请你在图中找出一对全等三角形,并写出证明它们全等的过程.

　31.某蛋糕生产厂家想就产品的价格以及质量进行一项简单的调查,调查问题为:你认为我厂生产的蛋糕是否品质纯正而且价格优惠? A.是;B.否。你觉得调查问题的设计有什么值得改进的地方吗?

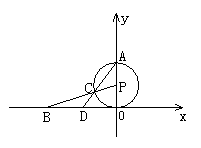
　32.已知:如图,⊙P与x轴相切于坐标原点O,点A(0,2)是⊙P与y轴的交点,点B(-2 ,0)在x轴上.连结BP交⊙P于点C,连结AC并延长交x轴于点D.

　　(1)求线段BC的长; (2)求直线AC的关系式;

　　(3)当点B在x轴上移动时,是否存在点B,使△BOP相似于△AOD?若存在,求出符合条件的点的坐标;若不存在,请说明理由.

四、学科间综合题:(6分)

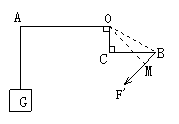
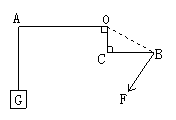
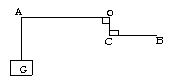
　33.如图所示的杠杆提起了300N的重物,O为支点,OA=5cm,OC=3cm,BC=4cm, 请在图中标出杠杆平衡的最小力的方向及大小.

参考答案:

一、1.C  2.C　3.A　4.A  5.C　6.C　7.C  8.C　9.C　10.A　11.B　12. A　13.A

二、14.x≤3且x≠2  15.(1,2)　16.y=x²+3x-4　17.-2　18.-7　19.ac>0　 20.54°　21.;　22.等腰　23.25　24.16cm²  25.2　26.810人

三、

27.解:(1)把A(2,2),B(5,2)分别代入y=x²+bx+c,可得,

解得.

　　(2)由b=-7,c=12,知y=x²-7x+12.

令y=0,得x²-7x+12=0,

∴x=3或x=4,∴C(3,0)或C(4,0).

　  (3)∵A(2,2),B(5,2),∴AB=│2-5│=3,  且△ABC的AB边上的高h=2,

∴=AB·h=×3×2=3.

28.解:由y=x+3,

取x=0,得y=3;取y=0,得x=2.

　∴二次函数图象经过(0,3),(2,0),(1,1)三点,把(0,3),(2,0),(1,1) 分别代入y=ax²+bx+c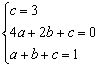,得,　解得

∴所求二次函数关系式为

y=.

29.证明:

(1)∵DE⊥BC,∠DBC=45°,∴BE=DE.

　　∵DE⊥BC,

∴∠2+∠C=90°,∠BEH=∠DEC=90°.

　　∵BF⊥CD,∴∠1+∠C=90°,∴∠1=∠2

　∴△BEH≌△DEC,∴BH=DC.

又∵ABCD,∴AB=DC,∴AB=BH.

(2)

∵ABCD,

∴AD∥BC,AB∥CD,∴∠1=∠G.

又∵BF⊥CD,

∴∠BFC=90°,∴∠ABG=∠BFC=90°.

　　又∵∠BEH=90°,∴∠BEH=∠GBA.

　　∴△BEH∽△GBA.∴,

　　又∵BH=AB,∴AB²=GA·HE.

30.△BCD≌△ACE.

证明:∵△ACB,△ECD都是等腰直角三角形,

∴∠BCD=∠ACE=90°,BC=AC,CD=CE.

　　∴△BCD≌△ACE.

31.“品质纯正”和“价格优惠”,可作为两个问题分别提问.

32.解:(1)如答图所示.

　　法一:由题意,得OP=1,BO=2,CP=1.在Rt△BOP中,

∵BP²=OP²+BO²,∴(BC+1)²=1²+ (2)²,

∴BC=2.

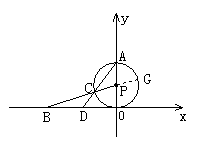
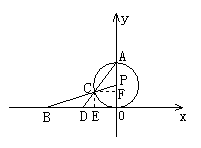
　　法二:延长BP交⊙P于G,如图所示,由题意,得OB=2,CG=2.

　 ∵OB²=BC·BG.

∴(2)²=BC·(BC+2),BC=2.

　　(2)如答图所示,过点C作CE⊥x轴于E,CF⊥y轴于F,

在△PBO中,∵CF∥BO,∴,

即,解得CF=.

同理可求得CE=.

　　因此C(-,),设直线AC的函数关系式为y=kx+b(k≠0),

把A(0,2),C(-,)两点代入关系式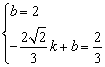,得, 解得.

　　∴所求函数关系式为y=x+2.

　　(3)如答图所示,在x轴上存在点B,使△BOP与△AOD相似.

∵∠OPB>∠OAD, ∴∠OPB≠∠OAD.

故若要△BOP与△AOD相似,

则∠OBP=∠OAD.

又∠OPB=2∠OAD,∴∠OPB= 2∠OBP.

　  ∵∠OPB+∠OBP=90°,∴3∠OBP=90°,∴∠OBP=30°.

因此OB=cot30°·OP=,

∴B₁点坐标为(-,0),

根据对称性可求得符合条件的B₂坐标(,0).

综上,符合条件的B点坐标有两个:

B₁ (-,0),B₂(,0).

四、33.解:由题意知,要使杠杆平衡,动力的方向应向下方,过B 点任作一动力F′(如答图),力臂长为OM,连接OB得一直角三角形OM,由于F′具有任意性, 所以使该杠杆平衡的动力的力臂都不会大于OB,故要使动力最小,可考虑以OB为动力臂. 具体方法是:过B点向下方作垂直于O,B连线的垂线,即得最小动力的方向,如答图所示,又在直角三角形OCB中,OC=3cm,BC=4cm,由勾股定理知OB=5cm,即OB=OA, 所以动力的大小为F=G=300N.