二○○六年淮安金湖基础教育课程改革实验区九年级
第二次诊断性调研考试试卷
数 学
欢迎你参加第二次诊断性调研考试试卷，祝你取得好成绩！请先看清以下几点注意事项：
1． 本卷分第Ⅰ卷和第Ⅱ卷两部分，共130分，考试时间为120分钟．
2．做第Ⅱ卷时，请先将密封线内的项目填写清楚，然后，用蓝色、黑色钢笔、签字笔或圆珠笔直接在试卷上作答，写在试题卷外无效．
3．考试结束后，将第I 卷、第II卷和答题卡一并交回。
第Ⅰ卷（选择题，共30分）
一、选择题：（每小题3分，共30分）
1.函数y=自变量x的取值范围是（ ）
A．x＞0 B．x＜0 C．x=0 D．x≠0
2. 下列计算不正确的是( )
A.（a－1）（－1－a）＝1－a2 B. a3＋2 a3＝3 a3
C.（a＋1）2＝a2＋1 D.（－a3）2÷a2＝a4
3. 设
，则实数a在数轴上对应的点的大致位置是（
）。
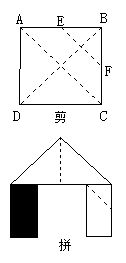
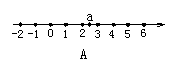
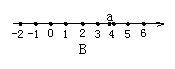
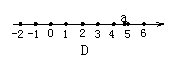
4. 如图，正方形硬纸片ABCD的边长是4，点E、F分别是AB、BC的中点，若沿左图中的虚线剪开，拼成如下右图的一座“小别墅”，则图中阴影部分的面积是（ ）。
（A）2 （B）4 （C）8 （D）10
5. 小兰和小潭分别用掷A、B两枚骰子的方法来确定P(
，
)的位置，她们规定：小兰掷得的点数为，小谭掷得的点数为，那么，她们各掷一次所确定的点落在已知直线
上的概率为( )
A、
B、
C、
D、
6. 二次三项式x2-4x+3配方的结果是 （ ）
A．(x-2)2+7 B．(x+2)2+7 C．(x-2)2-1 D．(x+2)2-1
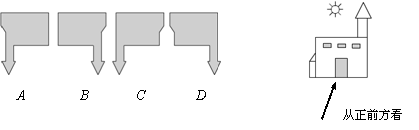
7. 如右图，太阳在房子的后方，那么你站在房子的正前方看到的影子为 ( )
 |
8. 第48届世乒赛刚刚在上海落幕，中国队再次囊括了五个单项的金牌。在有64名选手抽签分上下两个半区后，采用单淘汰的规程，最终笑傲群雄的是我国的王励勤，那么王励勤共打了（ ）场比赛获得冠军。
A. 4 B. 5 C.6 D.7
9. 如图是一张简易活动餐桌,现测得OA=OB=30cm，
OC=OD=50cm，现要求桌面离地面的高度为40cm，那么
两条桌腿的张角∠COD的大小应为 ( )
A．100°； B．120°； C．135°； D．150°.
10. 家在农村的小李家卖猪，为了揭露收购者短斤少两的行为，在收购者称一头猪重207斤并还没有被放下的时候，快速在猪身上放了事先称好的准确的10斤重的铁块，结果称得216斤。假设猪的实际重x斤，则根据题意，列方程得( )
A.
Ｂ．
Ｃ．
Ｄ．
第Ⅱ卷（100分）
二、填空题（本大题共6小题，每小题3分，共18分．把正确答案直接填在题中的横线上）
11. 
＝ ;
12 请写出一个根为x=1,另一个根满足-1﹤x﹤1的一元二次 方程______________________;
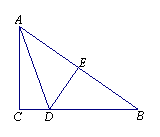
13. 如图，在△ABC中，∠C＝90°，AB的垂直平分线交BC于点D，如果∠CAD＝20°，那么∠B＝ °.
14．两圆的半径分别为3和4，圆心距为6，这两个圆的位置关系_________;
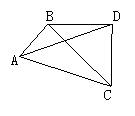
15．将一副三角尺如图摆放一起,连接AD, 则∠ADB的余切值为 .
16．如图，在一次军棋比赛中，如果团长所在的位置的坐标为（2，－5），司令所在的位置的坐标为（4，－2），那么工兵所在的位置的坐标为 ；
三．解答题 (本大题共11小题,共82分)
17． (本题满分5分)
计算：
－3tan600;
18． (本题满分5分) 计算 
;
19．(本题满分8分)
如图，BD是平行四边形ABCD的对角线（AD＞AB）
（1） 求作：∠A的平分线AE交CD的延长线于E点；（要求用尺规作图，保留作图痕迹，不写作法和证明）
（2）
设∠A的平分线AE交BD于F，试问
① 线段DE与图中哪一条线段相等？试说明理由；
② 求证：
=
。
20.(本题满分5分)
如图，在Rt△ABC中，∠BAC＝90°，AB＝1厘米， BC＝3厘米，将△ABC绕点A按逆时针方向旋转30°，得到△ADE，求点C运动了多少厘米.
 |
21．(本题满分7分)
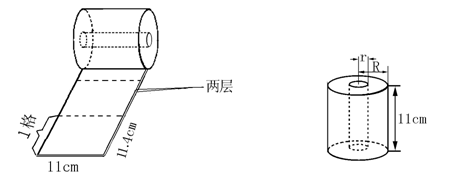
从“金莲”卫生纸的包装纸上得到以下资料：两层300格，每格11.4cm×11cm，如图甲。用尺量出整卷卫生纸的半径（
）与纸筒内芯的半径（
），分别为5.8cm和2.3cm，如图乙。那么该两层卫生纸的厚度为多少cm？（π取3.14，结果精确到0.001cm）
| ||||
| ||||
22．(本题满分7分)
黑、红、黄三种颜色涂在如下图所示的圆圈中，每个圆圈只能涂一种颜色，并且要使每条连线两端的圆圈上涂上不同的颜色，则共有多少种不同涂法？
23．(本题满分9分)
如图，已知直线y＝－x＋12分别交x轴、y轴于点A、B，将△AOB沿某直线折叠，使点A落在OB的中点处，折痕DE交OA于D，交OB于E，且AE：BE＝5：7.
（1）求AD的长；
（2）求△CDE的面积；
（3）若以点E为圆心，AE的长为半径作⊙E，
求⊙E在x轴上截得的弦AP的长.
24．(本题满分8分)
. 下表是县外国语七（1）班40位同学在“献爱心”活动中捐的图书情况记录
（单位：册）
| 2 | 8 | 9 | 6 | 5 | 4 | 3 | 3 |
| 11 | 10 | 12 | 10 | 12 | 3 | 4 | 9 |
| 12 | 3 | 5 | 10 | 11 | 2 | 12 | 7 |
| 2 | 9 | 12 | 8 | 7 | 12 | 11 | 4 |
| 12 | 10 | 5 | 3 | 2 | 8 | 10 | 12 |
（1）现需要将该班同学捐图书的情况，报告少先队大队部，请你给出一种表示这些数据的方案，使大队部一目了然知道整个情况？
（2）从（1）的方案中，请你至少写出三条获得的信息.
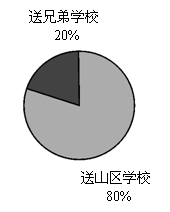（3）如果该班所捐图书准备按左边的扇形统计图所示的比例分送给山区学校和本市兄弟学校，则送给山区学校的图书有多少册？
25. (本题满分8分)
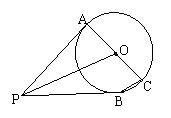
如图，AC是⊙O的直径，PA与⊙O相切于点A，点B在⊙O上，请将下列3个论断中的一个作为条件，另外两个作结论构造一个真命题，并加以证明。
（1）∠APO=∠BPO；
（2）BC∥OP；
（3）PB是⊙O的切线。
已知：AC是⊙O的直径，PA与⊙O相切于点A，点B在⊙O上，
求证：
。
26．(本题满分10分)
将二次函数
(如图)向右平移1个单位所得的二次函数的图象的顶点为点D，并与轴交于点A.
（1）写出平移后的二次函数的对称轴与点A的坐标；
（2）设平移后的二次函数的对称轴与函数的交点为点B，
试判断四边形OABD是什么四边形？请证明你的结论；
（3）能否在函数 的图象上找一点P，
使
DBP是以线段DB为直角边的直角三角形？
若能，请求出点P的坐标；若不能，请简要说明理由.
27．(本题满分10分)
在等腰梯形ABCD中，AB=DC=5，AD=4，BC=10. 点E在下底边BC上，点F在腰AB上.
（1）若EF平分等腰梯形ABCD的周长，设BE长为x，试用含x的代数式表示△BEF的面积；
（2）是否存在线段EF将等腰梯形ABCD的周长和面积同时平分？若存在，求出此时BE的长；若不存在，请说明理由；
（3）是否存在线段EF将等腰梯形ABCD的周长和面积同时分成1∶2的两部分？若存在，求出此时BE的长；若不存在，请说明理由.
