2006年嘉定区九年级数学学业考试模拟试卷
（考试时间100分钟，满分150分）
| 题号 | 一 | 二 | 三 | 四 | 总分 | |||||||
| 1-12 | 13-16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | ||
| 得分 | ||||||||||||
一、填空题（本题共12题，每题3分，满分36分）
1. 9的平方根是 .
2. 计算：
=
.
3. 函数
的定义域是
.
4. 已知
、
是方程
的两个根，则
.
5. 点P
关于
轴对称的点的坐标为
.
6. 若反比例函数
的图象经过点A
，则此函数解析式为
.
7. 若二次函数
的对称轴是直线
，则
= .
8. 若一组数据1、2、4、5、的平均数是4，则数为
.
9. 已知菱形的两条对角线的长分别为
、2，则此菱形的边长是 .
10. 在直角
ABC中，
=900，AC=8，
，则BC=
.
11. 半径分别为2cm和3cm两圆的圆心距为1cm，则这两圆的公切线共有 条.
12. 在RtACB中，
C=900，A=300，点D（与点A不重合）在边AC上，且AD<CD，若经过点D的直线截ACB所得的三角形与ACB相似，则这样的直线共有 条.
二、选择题（本题共4题，每题4分，满分16分）
13. 在下列化简中，正确的是 （ ）
（A）
（B）
（C）
（D）
14. 一次函数
的图象不经过下列各象限中的
（ ）
（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限
15. 下列命题中，假命题的是 （ ）
（A）平行四边形的对角线互相平分
（B）对角线互相平分的四边形是平行四边形
（C）矩形的对角线相等www.1230.org 初中数学资源网 收集整理
（D）对角线相等的四边形是矩形
16. 下列图形中是中心对称图形，但不是轴对称图形的是 （ ）
（A）角 （B）线段 （C）等边三角形 （D）平行四边形
三、（本题共5题，第17、18题每题9分，第19、20、21题每题10分，满分48分）
17. 计算：
;
18. 解方程组：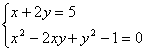
19. 最近某学校九年级某班的学生进行了一次数学测验，
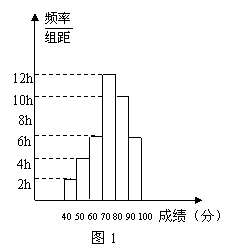其成绩大致分布情况如图1，此图是频率分布直方图
（每组含最低值，但不含最高值）.
请根据图形所提供的信息解答下列问题：
（1）这个班级的学生共有 人；
（2）在图1中，频率最小的分数段是 ；
（3）在图1中小长方形的 表示的是频率；
（4）这些成绩的中位数所在的分数段是 ；
（5）若成绩在80及80分以上的学生为优秀，
则这个班的优秀率为 （用百分比表示）.
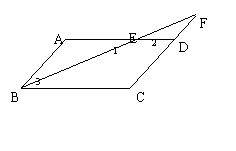
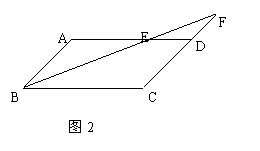20.如图2：在□ABCD中，A=1400， 直线BE交AD于点E，交CD的延长线于点F，且DE=DF.求F的度数.
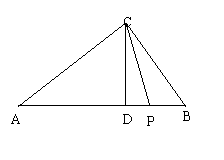
21.如图3：在RtACB中，C=900，AC=8，BC=6，CD是斜边AB上的高.
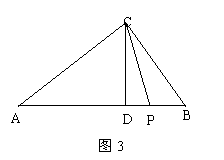若点P在线段DB上，连结CP，
=
.求CP的长.
四、（本题共4题，第22、23、24题每题12分，第25题14分，满分50分）
22.已知关于的方程
有两个不相等的实数根.
（1）求
的取值范围；（2）当取最大整数时，求方程的两个根.
23.如图4：AB是⊙O的直径，点P是AB延长线上一点，PD是⊙O的切线，切点为点D，连结OD，点C是⊙O上一点，且PC=PD.
（1）求证：直线PC是⊙O的切线；
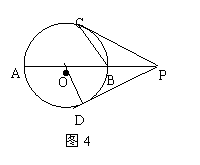（2）连结BC，CB=BP，PD=，求⊙O的半径.
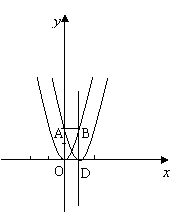
24.将二次函数
(如图5)向右平移1个单位所得的二次函数的图象的顶点为点D，并与
轴交于点A.
（1）写出平移后的二次函数的对称轴与点A的坐标；
（2）设平移后的二次函数的对称轴与函数的交点为点B，
试判断四边形OABD是什么四边形？请证明你的结论；
（3）能否在函数 的图象上找一点P，
使DBP是以线段DB为直角边的直角三角形？
若能，请求出点P的坐标；若不能，请简要说明理由.
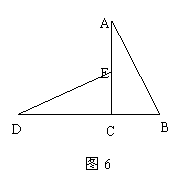
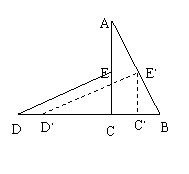
25.如图6：ACB与DCE是全等的两个直角三角形，其中ACB=DCE=900，AC=4，BC=2，点D、C、B在同一条直线上，点E在边AC上.
（1）直线DE与AB有怎样的位置关系？请证明你的结论；
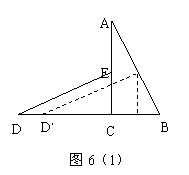
（2）如图6（1）若DCE沿着直线DB向右平移多少距离时，点E恰好落在边AB上，求平移距离DD，；
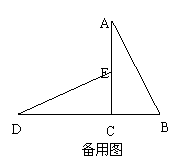
（3）在DCE沿着直线DB向右平移的过程中，使DCE与ACB的公共部分是四边形，设平移过程中的平移距离为，这个四边形的面积为，求与的函数关系式，并写出它的定义域.
 |
 |
参考答案与评分意见
一、1.
；2.
；3.
；4.
；5.；6.
；7.
；8.8；9.2；10.4
11.1；12.3.
二、13.C ； 14. A； 15.D； 16.D.
三、17.解：原式=
4分
=
3分
=
2分
18. 
解：由（2）得：
1分
即
或
2分
所以原方程组变为：
， 
2分
解这两个方程组得：
，
4分
19.（1）40；（2）40~50；（3）面积；（4）70~80；（5）40%. 每格2分
20.解：∵四边形ABCD是平行四边形
∴AB∥CF
∴∠3=∠F 2分
∵DE=DF
∴∠2=∠F 2分
∵∠1=∠2
∴∠3=∠1 2分
∵∠3+∠1+∠A=1800 1分
∵∠A=1400
∴∠3=200 2分
∴∠F=200 1分
21.解：在RtACB中，
∵C=900，AC=8，BC=6
∴AB=
=10 2分
∵CD是斜边AB上的高
∴
又
∴
2分
∴CD=
2分
在RtCDP中，
=
1分
∵=
∴
1分
∴CP=5 2分
四、22.解：（1）=
1分
=
=
1分
根据题意得：
1分
2分
又
1分
所以的取值范围为且
. 1分
（2）根据题意得：
1分
把
代入原方程得：
1分
即：
1分
解此方程得：
，
2分
所以当取最大整数时，此方程的两个根分别是：，.
23.（1）证明：连结OC 1分
在
和
中
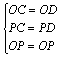
∴≌（S、S、S）2分
∴∠OCP=∠ODP 1分
∵PD是⊙O的切线
∴OD⊥PD 1分
∴∠ODP=900
∴∠OCP=900
1分
又OC是⊙O的半径
∴直线PC是⊙O的切线 1分
（2）∵CB=BP
∴∠1=∠2
∵∠OCP=900
∴∠4+∠2=900
∠1+∠3=900
∴∠3=∠4 1分
∴BO=BC
又BO=OC
∴
是等边三角形
∴∠3=600 1分
∵直线PC是⊙O的切线
PD是⊙O的切线
∴PC=PD 1分
∵PD=
∴PC=
在RtPCO中
1分
∴
∴OC=2 1分 即⊙O的半径为2
24.（1）平移后的二次函数的对称轴为直线 1分
点A的坐标（0，2） 1分
（2）四边形OABD是矩形. 1分
证明：把代入得：
∴点B的坐标为（1，2） 1分
| |
∴顶点D的坐标为（1，0） 1分
∴OA=DB=2
OA∥BD
∴四边形OABD是平行四边形 1分
又∠AOD=900
∴四边形OABD是矩形 1分
（3）能. 1分
当∠DBP=900时，∵四边形OABD是矩形∴∠DBA=900
即点P在直线AB上，直线AB为：
把代入得：
（正值舍去）
即点P的坐标为 2分
当∠PDB=900时，∵四边形OABD是矩形∴∠BDO=900
即点P在轴上，又点P在函数上，
所以点P与点O重合，
即点P的坐标为
2分
所以点P的坐标为、
25. （1）直线DE与AB垂直.
1分
证明：延长DE交AB于点F
∵ACB与DCE是全等的两个直角三角形
∴∠D=∠A 1分
∵ACB=900
∴∠A+∠B=900
∴∠D+∠B=900 1分
∴BFD=900 1分
∴直线DE与AB垂直.
（2）设平移距离DD，=
则CC，=，BC，=
1分
∵AC∥E，C，
∴
1分
又BC=2，EC=E，C，=2 AC=4
∴
1分
∴
1分
所以平移距离DD，为1.
（3）在DCE沿着直线DB向右平移的过程中
第一种情况：
如图当点E落在ACB内部或边AB上
设D，E，与边AC交于点G
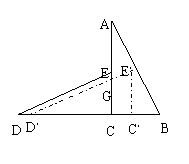∵DD，=
∴CD，=
由题意可知：D，G∥DE
∴
∽
∴
又 CD=4，
∴
∴
1分
∴
∴
1分 定义域为
1分
第二种情况
如图当点E落在ACB外部，且点C与点B重合或在CB的延长线上，
点D在线段CD上（与点C不重合）.
设D，E，分别交边AC、AB于点G、F
由第一种情况可知：
由（1）可知：D，F⊥AB
∴D，FB =ACB=900
又ABC=D，BF
∴
∽
∴
又 AB==
BD，=
∴
∴
1分
=
即：
1分
定义域为
1分