江苏省第十八届初中数学竞赛试题
初三年级
一、选择题(每小题7分,共42分)
1.在直角坐标系中,若一点的纵、横坐标都是整数,则称该点为整点.设k为整数,当直线y=x-2与y=kx+k的交点为整点时,k的值可以取( )
 (A)4个 (B)5个 (C)6个 (D)7个
(A)4个 (B)5个 (C)6个 (D)7个
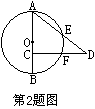
2.如图,AB是⊙O的直径,C为AB上的一个动点(C点不与A、B重合),
CD⊥AB,AD、CD分别交⊙O于E、F,则与AB·AC相等的一定是( )
(A)AE·AD (B)AE·ED (C)CF·CD (D)CF·FD
3.在△ABC与△A′B′C′中,已知AB<A′B′,BC<B′C′,CA<C′A′.下列结论:
(1)△ABC的边AB上的高小于△A′B′C′的边A′B′上的高;
(2)△ABC的面积小于△A′B′C′的面积;
(3)△ABC的外接圆半径小于△A′B′C′的外接圆半径;
(4)△ABC的内切圆半径小于△A′B′C′的内切圆半径.
其中,正确结论的个数为( )
(A)0 (B)1 (C)2 (D) 4
4.设![]() ,那么S与2的大小关系是( )
,那么S与2的大小关系是( )
(A)S=2 (B)S<2
(C)S>2 (D)S与2之间的大小与x的取值有关
5.折叠圆心为O、半径为10cm的圆纸片,使圆周上的某一点A与圆心O重合.对圆周上的每一点,都这样折叠纸片,从而都有一条折痕.那么,所有折痕所在直线上点的全体为( )
(A)以O为圆心、半径为10cm的圆周 (B)以O为圆心、半径为5cm的圆周
(C)以O为圆心、半径为5cm的圆内部分 (D)以O为圆心,半径为5cm的圆周及圆外部分
6.已知x,y,z都是实数,且x2+y2+z2=1,则m=xy+yz+zx( )
(A)只有最大值 (B)只有最小值
(C)既有最大值又有最小值 (D)既无最大值又无最小值
二、填空题(每小题7分,共56分)
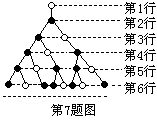 7.如图是一个树形图的生长过程,依据图中所示的生长规律,第15行的实心圆点的个数等于______.
7.如图是一个树形图的生长过程,依据图中所示的生长规律,第15行的实心圆点的个数等于______.
8.设0.![]() 为四位十进制纯小数,ai(i=1,2,3)只取0或1.记T是所有这些四位小数的个数 ,S是所有这些四位小数的和,则
为四位十进制纯小数,ai(i=1,2,3)只取0或1.记T是所有这些四位小数的个数 ,S是所有这些四位小数的和,则![]() =______.
=______.
9.如图,取一张长方形纸片,它的长AB=10cm,宽BC=5![]() cm,然后以虚线CE(E点在AD上)为折痕,使D点落在AB边上.则AE=_____cm,∠DCE=______°.
cm,然后以虚线CE(E点在AD上)为折痕,使D点落在AB边上.则AE=_____cm,∠DCE=______°.
10.直角三角形ABC中,∠A=90°,AB=5cm,AC=4cm,则∠A的平分线AD的长为______cm.

11.房间里有凳子(3条腿)、椅子(4条腿)若干张,每张凳子或椅子只能坐1人.一些人进来开会,只坐凳子或只坐椅子都不够坐,但每人都有椅子或凳子坐,且还有空位,已知人腿、凳腿、椅腿之和为32,则房间里共有______个人、______张凳子、______张椅子.
12.如图,⊙C通过原点,并与坐标轴分别交于A,D两点.已知∠OBA=30°,点D的坐标为(0,2),则点A,C的坐标分别为A( , );C( , ).
13.若关于x的方程rx2-(2r+7)x+(r+7)=0的根是正整数,则整数r的值可以是______.
14.将2,3,4,5,…,n(n为大于4的整数)分成两组,使得每组中任意两数之和都不是完全平方数.那么,整数n可以取得的最大值是______.
三、解答题(每题13分,共52分)
15.初三(8)班尚剩班费m(m为小于400的整数)元,拟为每位同学买1本相册.某批发兼零售文具店规定:购相册50本起可按批发价出售,少于50本则按零售价出售,批发价比零售价每本便宜2元,班长若为每位同学买1本,刚好用完m元;但若多买12本给任课教师,可按批发价结算,也恰好只要m元.问该班有多少名同学?每本相册的零售价是多少元?
16.已知关于x的方程x2+4x+3k-1=0的两个实根的平方和不小于这两个根的积;反比例函数![]() 的图像的两个分支在各自的象限内,点的纵坐标y随点的横坐标x的增大而减小.求满足上述条件的k的整数值.
的图像的两个分支在各自的象限内,点的纵坐标y随点的横坐标x的增大而减小.求满足上述条件的k的整数值.
17.求360的所有正约数的倒数和.
18.如图,在△ABC中,BC=6,AC=4![]() ,∠C=45°,P为BC上的动点,过P作PD∥AB交AC于点D,连结AP,△ABP、△APD、△CDP的面积分别记为S1,S2,S3,设BP=x.
,∠C=45°,P为BC上的动点,过P作PD∥AB交AC于点D,连结AP,△ABP、△APD、△CDP的面积分别记为S1,S2,S3,设BP=x.

(1)试用x的代数式分别表示S1,S2,S3;
(2)当P点位于BC上某处使得△APD的面积最大时,你能得出S1、S2、S3之间或S1、S2、S3两两之间的哪些数量关系(要求写出不少于3条)?
参考答案
一、选择题
1.A 2.A 3.A 4.D 5.D 6.C
二、填空题
7.377
8.0.0556
9.![]() ,30
,30
10.![]()
11.5,2,4
12.(![]() ,0),(
,0),(![]() ,1)
,1)
13.0,1或7
14.28
三、解答题
15.设该班共有x名同学,相册零售价每本y元.由题设,得
xy=(x+12)(y-2), ①
且整数x满足38<x<50. ②
由①得12y-2x-24=0,y=![]() +2,xy=
+2,xy=![]() +2x. ③
+2x. ③
由③及xy=m为整数,知整数x必为6的倍数,再由②,x只可能为42或48.
此时相应的y为9或10.
但m<400,
∴x=42,y=9.
答:(略).
16.由题意,方程x2+4x+3k-1=0 ①
有实数根,故△=42-4(3k-1)≥0,
解之,得k≤![]() . ②
. ②
设x1,x2为①的根,由根与系数关系知
x1+x2=-4,x1·x2=3k-1,
因![]() ≥x1x2,故
≥x1x2,故
(x1+x2)2-3x1x2≥0,
即(-4)2-3(3k-1)≥0,
∴k≤![]() . ③
. ③
又由![]() 当x>0或x<0时,分别随x值增大而减小,知
当x>0或x<0时,分别随x值增大而减小,知
1+5k>0,即k>-![]() . ④
. ④
综合②③④,得-![]() <k≤
<k≤![]() .
.
∴满足题中条件的k可取整数值为0, 1.
17.设正整数a的所有正约数之和为b,d1,d2,d3,…,dn为a的所有正约数从小到大的排列,于是d1=1,dn=a.由于
![]()
中各分数分母的最小公倍数为dn=a,故
![]() .
.
而a=360=23×32×5,故
b=(1+2+22+23)×(1+3+32)×(1+5)=1170,
∴360的所有正约数的倒数和为
![]() .
.
18.(1)由题意知:
BP=x,0<x<6,且有![]() ,
,
故AD=![]() ·BP=
·BP=![]() x=
x=![]() x.
x.
过P作PM⊥AC交AC于M点,过A作AN⊥BC交BC于N
点,则
PM=PC·sinC=(BC-PB)sin45°=![]() (6-x),
(6-x),
S2=S△APD=![]() AD·PM=
AD·PM=![]() ·
·![]() x·
x·![]() (6-x)=2x-
(6-x)=2x-![]() x2;
x2;
又AN=AC·sinC=4![]() ·sin45°=4,
·sin45°=4,
故S1=S△ABP=![]() BP·AN=2x;
BP·AN=2x;
S3=S△CDP=![]() CD·PM
CD·PM
=![]() (AC-AD)·PM
(AC-AD)·PM
=![]() (4
(4![]() -
-![]() x)·
x)·![]() (6-x)
(6-x)
=![]() (6-x)2.
(6-x)2.
(2)因为S2=2x-![]() x2=3-
x2=3-![]() (x-3)2,
(x-3)2,
所以当x=3时,S2取最大值S2=3,
此时S1=6,S3=3,
因此,S1,S2,S3之间的数量关系有S1=S2+S3,S2=S3,S1=2S2,S1=2S3.
(以上4个关系只要写出3个即可)