和平区2004--2005学年度第二学期九年级数学阶段检测试卷
第I卷(选择题 共30分)
一. 选择题:本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 我国陆地面积约为km2,用科学记数法可表示为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 下列图形中,既是中心对称图形,又是轴对称图形的共有( )
① 线段 ② 直角三角形 ③ 平行四边形 ④ 矩形 ⑤ 菱形 ⑥ 等腰梯形
A. 6个 B. 5个 C. 4个 D. 3个
3. 如图,四边形ABCD内接于⊙O,延长AB、DC相交于点E,延长AD、BC相交于点F,若![]() ,
,![]() ,则
,则![]() 等于(
)
等于(
)
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
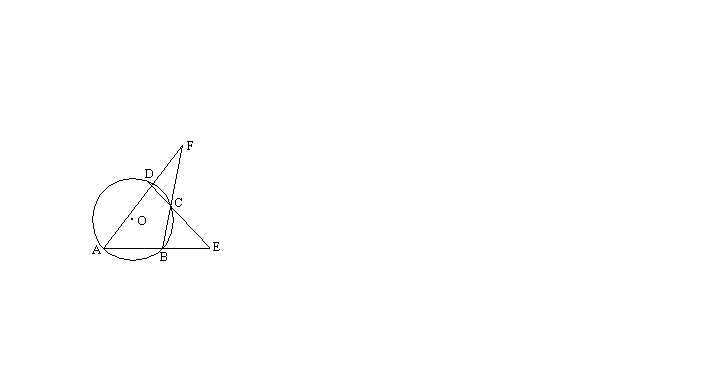
4. 已知![]() ,化简
,化简![]() 的结果是(
)
的结果是(
)
A. ![]() B.
B. ![]() C. 5
D.
C. 5
D. ![]()
5. 如图,在![]() 中,点E在AC上,且EC=2AE,F是BE的中点,AF的延长线交BC于点D。则有()
中,点E在AC上,且EC=2AE,F是BE的中点,AF的延长线交BC于点D。则有()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
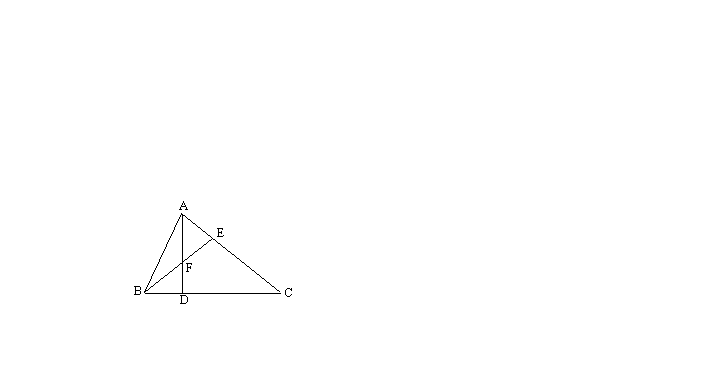
6. 已知二次函数的图象经过![]() ,
,![]() ,
,![]() 三点,则该函数解析式为(
)
三点,则该函数解析式为(
)
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
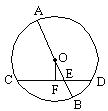
7. 如图,⊙O的直径AB=10,E是OB上一点,弦CD过点E,且BE=2,![]() ,则弦心距OF等于( )
,则弦心距OF等于( )
A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
8. 一组数据15,17,14,10,15,17,17,16,14,12,其平均数为a,中位数为b,众数为c,则有()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9. 已知关于x的方程![]() 有实数根,则m的取值范围是( )
有实数根,则m的取值范围是( )
A. ![]() B.
B. ![]() 且
且![]() C.
C. ![]() D.
D. ![]()
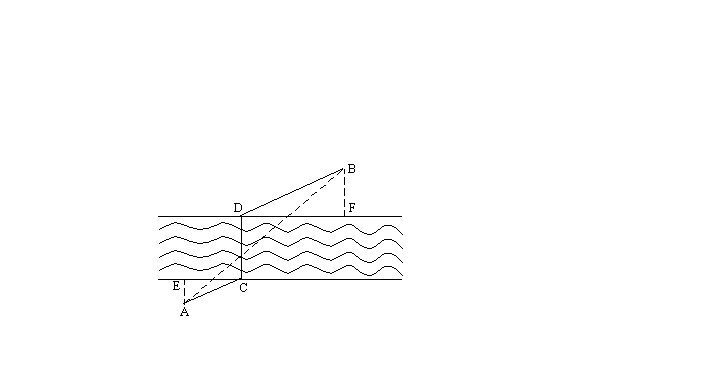
10. 如图,旅游景点A、B位于河的两侧,其直线距离为150米,景点A与河岸距离AE=15米,景点B与河岸距离BF=35米,河宽为40米,现选取适当位置垂直于河两岸建一座长与河宽相等的小桥CD,使连接景点A、B的路程AC+CD+DB最短,则最短路程为()
A. 160米 B. 170米 C. 180米 D. 190米
第II卷(非选择题 共90分)
二. 填空题:本大题共8小题,每小题3分,共24分。请将答案直接填在题中横线上。
11. 在![]() 中,
中,![]() ,若
,若![]() ,则
,则![]() 。
。
12. 在半径![]() 的圆中,
的圆中,![]() 的圆心角所对的弧长为
cm。
的圆心角所对的弧长为
cm。
13. 不等式组![]() 的解集是
。
的解集是
。
14. 如图,矩形ABCD的周长为16cm,E在AD上,F在AB上,且![]() ,EF=EC,DE=2cm,则AE=
。
,EF=EC,DE=2cm,则AE=
。
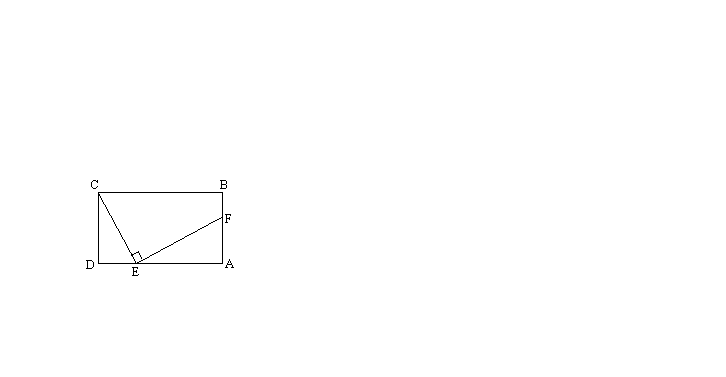
15. 无论k取何值,直线![]() 必经过某一定点,则这个定点的坐标为
。
必经过某一定点,则这个定点的坐标为
。
16. 甲、乙两人加工一批零件,甲5小时加工的数量与乙9小时加工的数量相等,现乙加工2小时后甲才开始加工,当两人加工的数量相等时,甲加工了 小时。
17. 如图,已知在四边形ABCD中,![]() ,且
,且![]() ,
,![]() ,则四边形ABCD面积的最大值为 。
,则四边形ABCD面积的最大值为 。

18. 已知![]() ,
,![]() ,则
,则![]() 。
。
三. 解答题:本大题共8小题,共66分。解答应写出文字说明、演算步骤或证明过程。
19.(本题6分)
如图,在![]() 中,已知
中,已知![]() ,
,![]() ,延长BC至D点,使CD=CA,连结AD。求
,延长BC至D点,使CD=CA,连结AD。求![]() 的度数。
的度数。
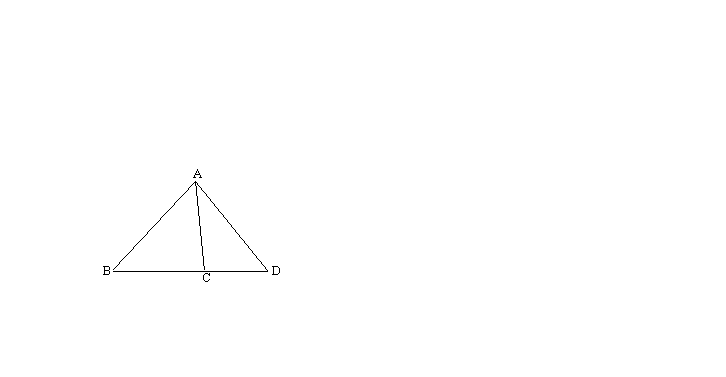
20.(本题8分)
解方程![]()
21.(本小题8分)
如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交
的图象交![]() 、
、![]() 两点。求:(1)一次函数的解析式;(2)
两点。求:(1)一次函数的解析式;(2)![]() 的面积。
的面积。
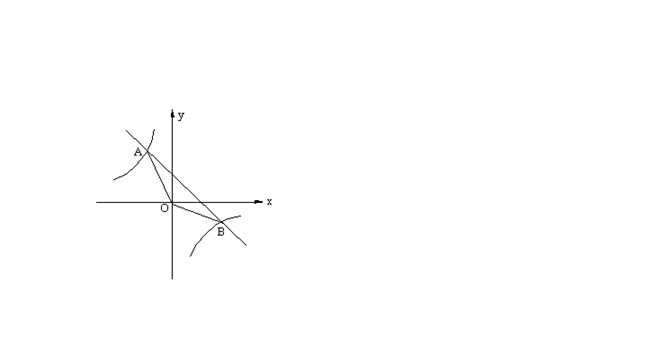
22.(本小题8分)
为落实“珍惜和合理利用每一寸土地”的国策,某地区计划经过若干年开发改造后可利用土地360km2,实际施工中,每年比原计划多开发2km2,按此进度,预计可提前6年完成开发任务,问实际每年开发多少km2?
23.(本小题8分)
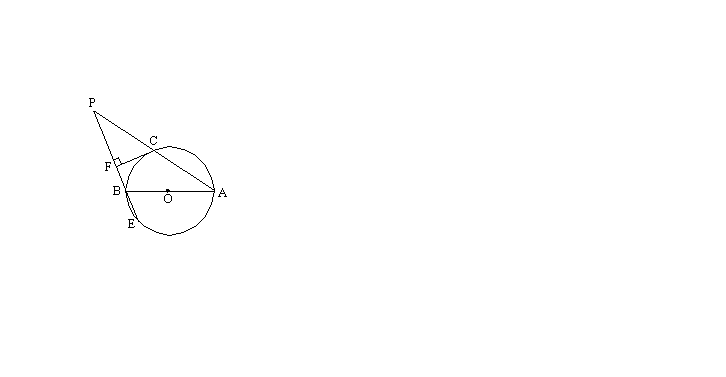
如图,AB为⊙O的直径,P为⊙O外一点,PA交⊙O于C点,PB延长线交⊙O于E点,CF切⊙O于C点,且![]() 于F点,若
于F点,若![]() ,
,![]() 。
。
求:(1)BF和PA的长;(2)![]() 的面积。
的面积。
24.(本小题8分)
如图,厂房屋顶人字架(等腰三角形)的跨度为10m,![]() ,求中柱BC(C为底边中点)和上弦AB的长(精确到0.01m)。
,求中柱BC(C为底边中点)和上弦AB的长(精确到0.01m)。
参考数据:![]()
![]()
![]()
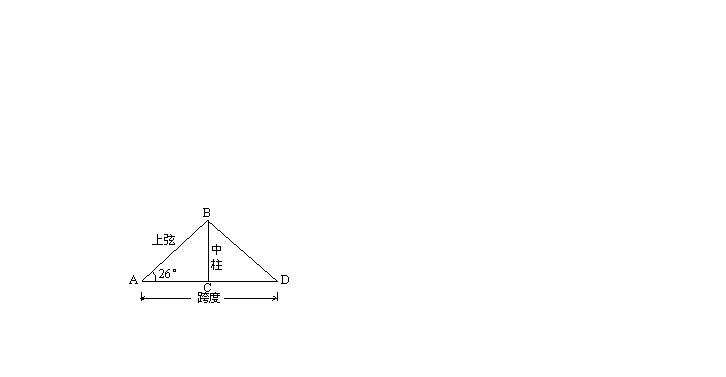
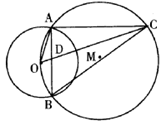
25.(本小题10分)
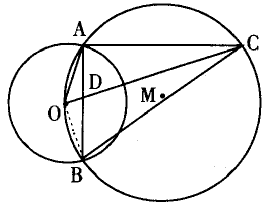
如图,⊙O与⊙M相交于A、B两点,点O在⊙M上,⊙M的弦OC交AB于点D。
(1)求证:![]()
(2)设⊙O的半径为r,若![]() 。求证:
。求证:![]() 。
。
26.(本小题10分)
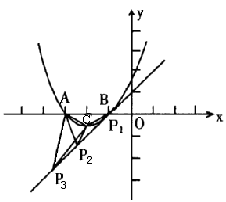
在如图所示的直角坐标系中,已知抛物线![]() 与x轴的负半轴交于A、B两点,且
与x轴的负半轴交于A、B两点,且![]() 。
。
(1)求抛物线的解析式;
(2)若直线![]() 与抛物线只有一个交点,试确定a的值;
与抛物线只有一个交点,试确定a的值;
(3)设抛物线的顶点为C,在(2)中直线上是否存在点P,使![]() 是等腰三角形?如果存在,请写出所有满足条件的点P的坐标;如果不存在,请说明理由。
是等腰三角形?如果存在,请写出所有满足条件的点P的坐标;如果不存在,请说明理由。
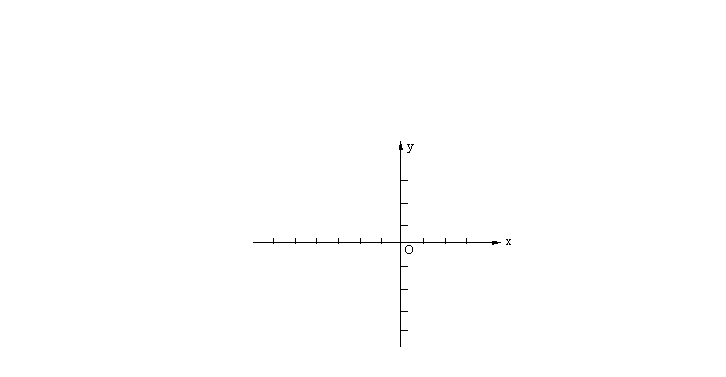
和平区2004�2005学年度第二学期九年级
数学阶段检测试卷标准答案与评分标准
一. 选择题(本大题共10小题,每小题3分,共30分)
1. C 2. D 3. B 4. A 5. C 6. D 7. D 8. A
9. C 10. B
二. 填空题(本大题共8小题,每小题3分,共24分)
11. ![]() 12 .
12 . ![]() 13.
13. ![]() 14.
14. ![]() 15.
15. ![]()
16. 2.5 17. ![]() 18.
18. ![]()
三. 解答题(本大题共8小题,共66分)
19.(本小题6分)
解:∵ ![]() ∴
∴
![]() (2分)
(2分)
∵ ![]() ∴
∴
![]() (3分)
(3分)
在![]() 中,∵
中,∵
![]() ,
,![]()
∴ ![]() (5分)
(5分)![]() (6分)
(6分)
20.(本小题8分)
解:设![]() ,那么
,那么![]() ,于是有
,于是有![]() ,即
,即![]() (1分)
(1分)
解这个方程得![]() ,
,![]() (3分)
(3分)
当![]() 时,
时,![]() ,整理得
,整理得![]() ∵
∵
![]()
∴ 此方程无实根 (5分) 当![]() 时,
时,![]() ,整理得
,整理得![]()
∴ ![]() ,
,![]() (7分)
(7分)
经检验,![]() ,
,![]() 均是原方程的根
均是原方程的根
∴ 原方程的根是![]() ,
,![]() (8分)
(8分)
21.(本小题8分)
解:
(1)∵ ![]() 过点
过点![]() 和
和![]() ∴
∴
![]() ,
,![]()
即![]() ,
,![]() (2分)
(2分)
根据题意,得![]()
解得![]() (4分)
(4分)
∴ 一次函数解析式为![]() (5分)
(5分)
(2)设![]() 与
与![]() 轴交点为C,则
轴交点为C,则![]() (6分)
(6分)
![]()
![]()
![]() (8分)
(8分)
22.(本小题8分)
解:设实际每年开发x km2,则原计划每年开发![]() (1分)
(1分)
根据题意得![]() (4分)
(4分)
化简并整理得![]() (5分)
(5分)
解得![]() ,
,![]() (6分)
(6分)
经检验![]() ,
,![]() 是原方程的根,但
是原方程的根,但![]() 不合题意,舍去(7分)
不合题意,舍去(7分)
答:实际每年开发![]() (8分)
(8分)
23.(本小题8分)
解:
(1)连结BC,∵ AB为⊙O的直径 ∴ ![]() (1分)
(1分)
∵ 在![]() 中,
中,![]() ∴
∴
![]()
∵ ![]() ∴
∴
![]() (2分)
(2分)
∴ ![]()
![]()
则BF、PF为方程![]() 的两根
的两根
解方程,得![]() ,
,![]() (4分)
(4分)
由切割线定理,得![]()
∴ ![]() ,
,![]()
∴ ![]() ,
,![]() (5分)
(5分)
∴ ![]()
∴ ![]() ,
,![]() (6分)
(6分)
(2)∵ ![]() ,
,![]() ∴
∴
![]() (7分)
(7分)
∴ ![]() (8分)
(8分)
24.(本小题8分)
解:∵ ![]() (2分)
(2分)
∴ ![]()
![]() (4分)
(4分)
∵ ![]() (5分)
(5分)
∴ ![]()
![]() (7分)
(7分)
答:中柱BC约长2.44m,上弦AB约长5.56m (8分)
25.(本小题10分)
证明:
(1)连结OB ∵ OA=OB ![]() ∴
∴
![]()
∴ ![]() (2分) 又
(2分) 又 ![]()
∴ ![]() ~
~![]() (4分) ∴
(4分) ∴ ![]() ∴
∴
![]() (5分)
(5分)
(2)∵ ![]() ~
~![]() ∴
∴
![]() ∴
∴
![]() (6分)
(6分)
同理得![]() (7分)
(7分)
∴ ![]() 即
即![]() (8分)
(8分)
∵ ![]() ,
,![]() ∴
∴
![]() (10分)
(10分)
26.(本小题10分)
(1)解:设抛物线与x轴负半轴交于点![]() ,
,![]()
![]()
依题意,得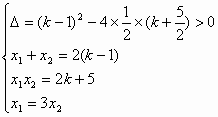
解得![]() ,
,![]() (2分)
(2分)
而![]() 时,使
时,使![]() ,不合题意,舍去
,不合题意,舍去
∴ ![]() 为所求
(3分)
为所求
(3分)
(2)解:依题意,得 只有一个解
只有一个解
(2)-(1),化简得![]() (4分)
(4分)
∴ ![]() ∴
∴
![]() ,
,![]() (5分)
(5分)
∵ ![]() ∴
∴
![]() (6分)
(6分)
(3)如图,抛物线![]() 与x轴的交点
与x轴的交点![]() ,
,![]()
配方得![]() ∴
抛物线的顶点
∴
抛物线的顶点![]() (7分)
(7分)
∴ 存在满足条件的点P,使![]() 为等腰三角形,它们是:
为等腰三角形,它们是:![]() ,
,![]() ,
,![]() (10分)
(10分)