练习二十二·代数·二次函数及其图像（二）
班级________姓名_________学号____________
一、 填空题
1．抛物线y=x2+3x-10的顶点坐标是__________,与y轴交点坐标是__________,与x轴交点坐标是__________.
2.二次函数y=ax2+4x+a的最大值是3,则a=__________.
3将抛物线y=3(x+3)2-5向_________平移__________个单位,向_________平移________个单位,
才能使顶点在原点.
4.函数y=x2-4x+3的图像的顶点及它和x轴的两个交点为顶点所构成的三角形面积为______平方单位.
5.已知抛物线y=ax2+bx+c,经过(-3,0),(1,0)及(0,4)三点,则解析式为_________.
二、选择题
1．已知抛物线的顶点坐标为（2，1），且抛物线经过点（3，0），则这条抛物线的解析式是（ ）.
（A）
（B）
（C）y=x2-4x+5 （D）y=-x2+4x-3
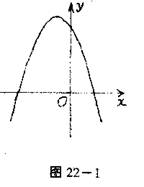
2．抛物线y=ax2+bx+c（a≠0）的图像如图22-1，那么（ ）.
（A） a＜0，b＞0，c＞0（B）a＜0，b＜0，c＞0
（B）a＜0，b＞0，c＜0（D）a＜0，b＜0，c＜0
3．二次函数y=mx2+2mx-（3-m）的图像如图22-2，那么m的取值范围是（ ）
（A）m＞0（B）m＞3（C）m＜0（D）0＜m＜3
4．函数y=ax2与y=ax+a（a＜0＝在同一直角坐标系中的图像大致是图22-3中的（ ）
.
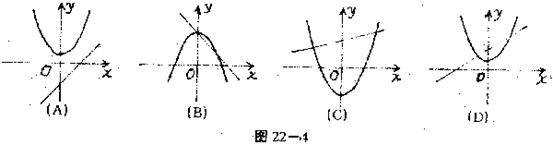
5.函数y=ax2+b与y=ax+b(a≠0，a，b为常数)在同一直角坐标系中的图像大致是图22-4中的（ ）
三、解答题
6．已知抛物线经过A（1，-4），B（7，8），C（-5，20）三点，求二次函数的解析式.
7．已知抛物线顶点（3，3），且过点（1，1），求此抛物线的解析式.
8．已知二次函数图像与x轴交点坐标是（-2，0），（1，0），且过点（2，8），求此二次函数的解析式.
9．抛物线过A（2，8），B（0，-4），且在x轴上截得的线段长为3，求此抛物线的解析式.
四、解答题
15． 作出函数y=x2+4x-5的图像，并说明当x取哪些值时，函数值（1）大于零；（2）小于零；
（3）等于零；（4）y随x的增大而增大.
16． 已知二次函数y=ax2+bx+c，其图像顶点坐标是（-2，-4），且抛物线过原点，求此二次函数的解析式.
17． 二次函数y=ax2+bx+c的最大值等于-3a，且它的图像经过（-1，-2），（1，6）两点，求a，b，c.
18．
已知二次函数y=ax2+bx+c的图像经过一次函数y=
的图像与x轴、y轴的交点，
并且经过点（1，1），求这个二次函数的解析式，并用配方法将解析式化为y=a（x-h）2+k的形式.